Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 118120 by bemath last updated on 15/Oct/20

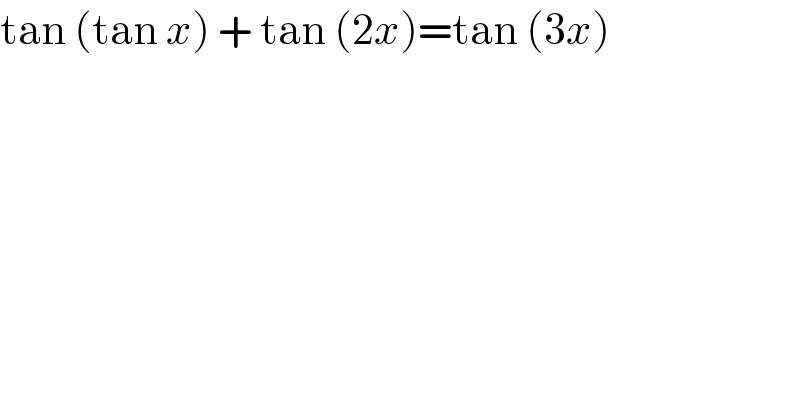
tan (tan x) + tan (2x)=tan (3x)

$$\mathrm{tan}\:\left(\mathrm{tan}\:{x}\right)\:+\:\mathrm{tan}\:\left(\mathrm{2}{x}\right)=\mathrm{tan}\:\left(\mathrm{3}{x}\right) \\ $$

Commented by MJS_new last updated on 15/Oct/20

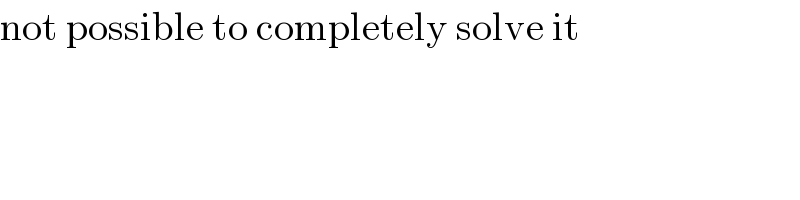
not possible to completely solve it

$$\mathrm{not}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{completely}\:\mathrm{solve}\:\mathrm{it} \\ $$

Answered by TANMAY PANACEA last updated on 15/Oct/20

tanx=t tant=((3t−t^3 )/(1−3t^2 ))−((2t)/(1−t^2 )) tant=((3t−3t^3 −t^3 +t^5 −2t+6t^3 )/(1−t^2 −3t^2 +3t^4 ))=((t^5 +2t^3 +t)/(3t^4 −4t^2 +1)) tant=((t(t^2 +1)^2 )/((1−3t^2 )(1−t^2 ))) right hand side =∞ when t^2 =1 or t^2 =(1/3) then Left hand side should also be ∞ but left hand side is tan(1) or tan((1/( (√3)))) so = sign not hold hence t^2 ≠1 or t^2 ≠(1/3) tanx≠ ±1 tanx≠ ±(1/( (√3))) now let t=0 right hand side=0 left hand side also tan(0)=0 so solution is feasible when t=0 tanx=0 x=0

$${tanx}={t} \\ $$$${tant}=\frac{\mathrm{3}{t}−{t}^{\mathrm{3}} }{\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} }−\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$${tant}=\frac{\mathrm{3}{t}−\mathrm{3}{t}^{\mathrm{3}} −{t}^{\mathrm{3}} +{t}^{\mathrm{5}} −\mathrm{2}{t}+\mathrm{6}{t}^{\mathrm{3}} }{\mathrm{1}−{t}^{\mathrm{2}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{3}{t}^{\mathrm{4}} }=\frac{{t}^{\mathrm{5}} +\mathrm{2}{t}^{\mathrm{3}} +{t}}{\mathrm{3}{t}^{\mathrm{4}} −\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${tant}=\frac{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{3}{t}^{\mathrm{2}} \right)\left(\mathrm{1}−{t}^{\mathrm{2}} \right)} \\ $$$$\:\boldsymbol{{right}}\:\boldsymbol{{hand}}\:\boldsymbol{{side}}\:=\infty\:\:{when}\:{t}^{\mathrm{2}} =\mathrm{1}\:\:\:{or}\:{t}^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${then}\:{Left}\:{hand}\:{side}\:{should}\:{also}\:{be}\:\infty \\ $$$$\boldsymbol{{but}}\:\boldsymbol{{left}}\:\boldsymbol{{hand}}\:\boldsymbol{{side}}\:\boldsymbol{{is}}\:\boldsymbol{{tan}}\left(\mathrm{1}\right)\:\:\:\boldsymbol{{or}}\:\boldsymbol{{tan}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$\boldsymbol{{so}}\:=\:\boldsymbol{{sign}}\:\boldsymbol{{not}}\:\boldsymbol{{hold}} \\ $$$$\boldsymbol{{hence}}\:{t}^{\mathrm{2}} \neq\mathrm{1}\:\:\:{or}\:{t}^{\mathrm{2}} \neq\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${tanx}\neq\:\:\:\pm\mathrm{1}\:\:\:{tanx}\neq\:\:\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\: \\ $$$$\boldsymbol{{now}}\:\:\boldsymbol{{let}}\:\boldsymbol{{t}}=\mathrm{0}\:\:\boldsymbol{{right}}\:\boldsymbol{{hand}}\:\boldsymbol{{side}}=\mathrm{0} \\ $$$$\boldsymbol{{left}}\:\boldsymbol{{hand}}\:\boldsymbol{{side}}\:\boldsymbol{{also}}\:\boldsymbol{{tan}}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\:\boldsymbol{{so}}\:\boldsymbol{{solution}}\:\boldsymbol{{is}}\:\boldsymbol{{feasible}}\:\:\boldsymbol{{when}}\:\boldsymbol{{t}}=\mathrm{0} \\ $$$$\boldsymbol{{tanx}}=\mathrm{0}\:\:\boldsymbol{{x}}=\mathrm{0} \\ $$

Commented by 1549442205PVT last updated on 15/Oct/20

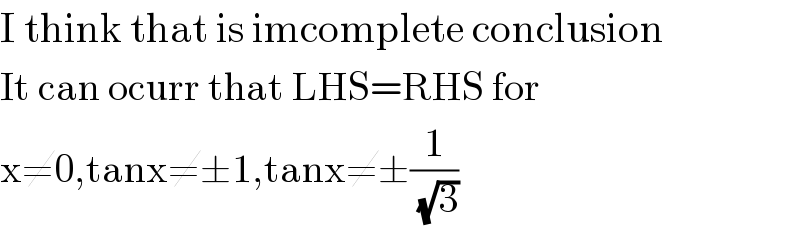
I think that is imcomplete conclusion It can ocurr that LHS=RHS for x≠0,tanx≠±1,tanx≠±(1/( (√3)))

$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{is}\:\mathrm{imcomplete}\:\mathrm{conclusion} \\ $$$$\mathrm{It}\:\mathrm{can}\:\mathrm{ocurr}\:\mathrm{that}\:\mathrm{LHS}=\mathrm{RHS}\:\mathrm{for} \\ $$$$\mathrm{x}\neq\mathrm{0},\mathrm{tanx}\neq\pm\mathrm{1},\mathrm{tanx}\neq\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$

Commented by TANMAY PANACEA last updated on 15/Oct/20

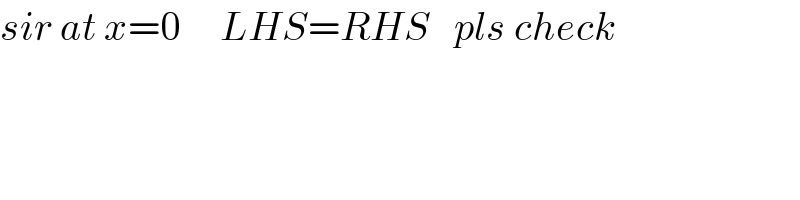
sir at x=0 LHS=RHS pls check

$${sir}\:{at}\:{x}=\mathrm{0}\:\:\:\:\:{LHS}={RHS}\:\:\:{pls}\:{check} \\ $$

Commented by prakash jain last updated on 15/Oct/20

https://www.wolframalpha.com/input/?i=tan+%28tan+x%29+%2B+tan+%282x%29%3Dtan+%283x%29

Commented by MJS_new last updated on 15/Oct/20

I don′t think Wolfram Alpha found all solutions

$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{think}\:\mathrm{Wolfram}\:\mathrm{Alpha}\:\mathrm{found}\:{all}\:\mathrm{solutions} \\ $$

Commented by prakash jain last updated on 15/Oct/20

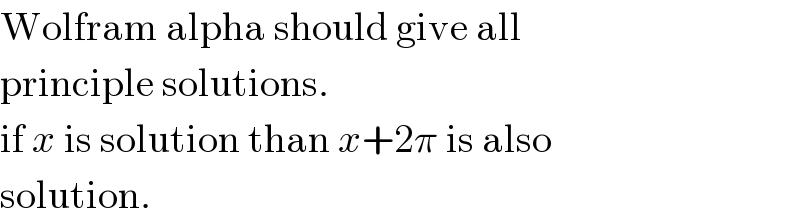
Wolfram alpha should give all principle solutions. if x is solution than x+2π is also solution.

$$\mathrm{Wolfram}\:\mathrm{alpha}\:\mathrm{should}\:\mathrm{give}\:\mathrm{all} \\ $$$$\mathrm{principle}\:\mathrm{solutions}. \\ $$$$\mathrm{if}\:{x}\:\mathrm{is}\:\mathrm{solution}\:\mathrm{than}\:{x}+\mathrm{2}\pi\:\mathrm{is}\:\mathrm{also} \\ $$$$\mathrm{solution}. \\ $$

Commented by MJS_new last updated on 15/Oct/20

look at the interval [0; (π/2)] we have 0≤tan x<+∞ ⇒ tan tan x runs through ]−∞; +∞[ infinite times ⇒ we could get infinite solutions for the given equation, most of them very close to x=(π/2)∧x<(π/2). I′m not 100% sure but...

$$\mathrm{look}\:\mathrm{at}\:\mathrm{the}\:\mathrm{interval}\:\left[\mathrm{0};\:\frac{\pi}{\mathrm{2}}\right] \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{0}\leqslant\mathrm{tan}\:{x}<+\infty \\ $$$$\left.\Rightarrow\:\mathrm{tan}\:\mathrm{tan}\:{x}\:\mathrm{runs}\:\mathrm{through}\:\right]−\infty;\:+\infty\left[\:\mathrm{infinite}\right. \\ $$$$\mathrm{times}\:\Rightarrow\:\mathrm{we}\:\mathrm{could}\:\mathrm{get}\:\mathrm{infinite}\:\mathrm{solutions}\:\mathrm{for} \\ $$$$\mathrm{the}\:\mathrm{given}\:\mathrm{equation},\:\mathrm{most}\:\mathrm{of}\:\mathrm{them}\:\mathrm{very}\:\mathrm{close} \\ $$$$\mathrm{to}\:{x}=\frac{\pi}{\mathrm{2}}\wedge{x}<\frac{\pi}{\mathrm{2}}.\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{100\%}\:\mathrm{sure}\:\mathrm{but}... \\ $$

Commented by MJS_new last updated on 15/Oct/20

look at the sequence of full periods (m, n ∈Z) tan tan x =0 ⇒ x=mπ+arctan nπ let m=0 x_n =arctan nπ x_0 =0 x_1 ≈1.26263 x_2 ≈1.41297 x_3 ≈1.46509 x_4 ≈1.49139 x_5 ≈1.50722 ... x_(10) ≈1.53898 x_(100) ≈1.56761 x_(1000) ≈1.57048 x_(+∞) =(π/2) in each interval we could have a solution for tan tan x =tan 3x −tan 2x

$$\mathrm{look}\:\mathrm{at}\:\mathrm{the}\:\mathrm{sequence}\:\mathrm{of}\:\mathrm{full}\:\mathrm{periods}\:\left({m},\:{n}\:\in\mathbb{Z}\right) \\ $$$$\mathrm{tan}\:\mathrm{tan}\:{x}\:=\mathrm{0}\:\Rightarrow\:{x}={m}\pi+\mathrm{arctan}\:{n}\pi \\ $$$$\mathrm{let}\:{m}=\mathrm{0} \\ $$$${x}_{{n}} =\mathrm{arctan}\:{n}\pi \\ $$$${x}_{\mathrm{0}} =\mathrm{0} \\ $$$${x}_{\mathrm{1}} \approx\mathrm{1}.\mathrm{26263} \\ $$$${x}_{\mathrm{2}} \approx\mathrm{1}.\mathrm{41297} \\ $$$${x}_{\mathrm{3}} \approx\mathrm{1}.\mathrm{46509} \\ $$$${x}_{\mathrm{4}} \approx\mathrm{1}.\mathrm{49139} \\ $$$${x}_{\mathrm{5}} \approx\mathrm{1}.\mathrm{50722} \\ $$$$... \\ $$$${x}_{\mathrm{10}} \approx\mathrm{1}.\mathrm{53898} \\ $$$${x}_{\mathrm{100}} \approx\mathrm{1}.\mathrm{56761} \\ $$$${x}_{\mathrm{1000}} \approx\mathrm{1}.\mathrm{57048} \\ $$$${x}_{+\infty} =\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{in}\:\mathrm{each}\:\mathrm{interval}\:\mathrm{we}\:\mathrm{could}\:\mathrm{have}\:\mathrm{a}\:\mathrm{solution} \\ $$$$\mathrm{for}\:\mathrm{tan}\:\mathrm{tan}\:{x}\:=\mathrm{tan}\:\mathrm{3}{x}\:−\mathrm{tan}\:\mathrm{2}{x} \\ $$

Commented by prakash jain last updated on 16/Oct/20

I think only correct priciple solution is 0 as Tanmay mentioned. I did some manual calculation and values becomes very close to zero but that is because i am subtracting tan3x fom tan2x. It is exactly 0 only at 0 between [0,π)

$$\mathrm{I}\:\mathrm{think}\:\mathrm{only}\:\mathrm{correct}\:\mathrm{priciple}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{0} \\ $$$$\mathrm{as}\:\mathrm{Tanmay}\:\mathrm{mentioned}. \\ $$$$\mathrm{I}\:\mathrm{did}\:\mathrm{some}\:\mathrm{manual}\:\mathrm{calculation}\:\mathrm{and} \\ $$$$\mathrm{values}\:\mathrm{becomes}\:\mathrm{very}\:\mathrm{close}\:\mathrm{to}\:\mathrm{zero} \\ $$$$\mathrm{but}\:\mathrm{that}\:\mathrm{is}\:\mathrm{because}\:\mathrm{i}\:\mathrm{am}\:\mathrm{subtracting} \\ $$$$\mathrm{tan3x}\:\mathrm{fom}\:\mathrm{tan2x}. \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{exactly}\:\mathrm{0}\:\mathrm{only}\:\mathrm{at}\:\mathrm{0}\:\mathrm{between} \\ $$$$\left[\mathrm{0},\pi\right) \\ $$

Commented by MJS_new last updated on 17/Oct/20

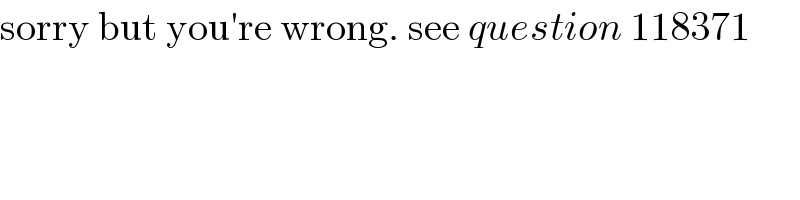
sorry but you′re wrong. see question 118371

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{you}'\mathrm{re}\:\mathrm{wrong}.\:\mathrm{see}\:{question}\:\mathrm{118371} \\ $$

Commented by prakash jain last updated on 17/Oct/20

Yes. I made calculation error. Realize it now.

$$\mathrm{Yes}.\:\mathrm{I}\:\mathrm{made}\:\mathrm{calculation}\:\mathrm{error}. \\ $$$$\mathrm{Realize}\:\mathrm{it}\:\mathrm{now}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com