Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 11834 by Mr Chheang Chantria last updated on 02/Apr/17

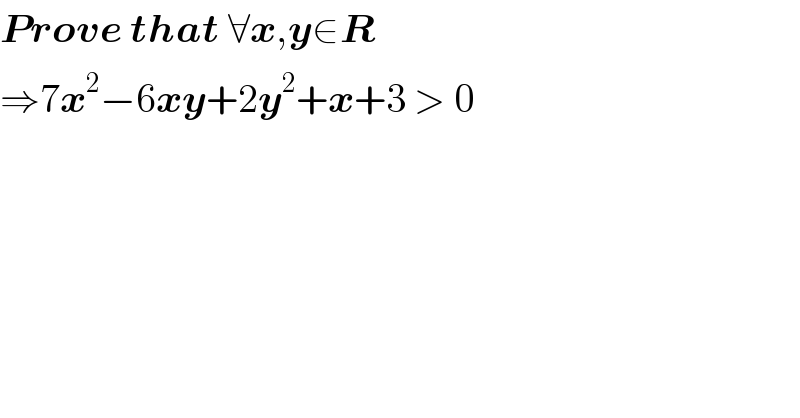
Prove that ∀x,y∈R ⇒7x^2 −6xy+2y^2 +x+3 > 0

$$\boldsymbol{{Prove}}\:\boldsymbol{{that}}\:\forall\boldsymbol{{x}},\boldsymbol{{y}}\in\boldsymbol{{R}} \\ $$ $$\Rightarrow\mathrm{7}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{xy}}+\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{x}}+\mathrm{3}\:>\:\mathrm{0} \\ $$

Answered by mrW1 last updated on 02/Apr/17

7x^2 −6xy+2y^2 +x+3 =((3/(√2))x)^2 −2×(3/(√2))x×(√2)y+((√2)y)^2 +((1/2)x)^2 +2×(1/2)x+1+[7−((3/(√2)))^2 −((1/2))^2 ]x^2 +(3−1) =((3/(√2))x−(√2)y)^2 +((1/2)x+1)^2 +((3/2)x)^2 +2 >2>0

$$\mathrm{7}\boldsymbol{{x}}^{\mathrm{2}} −\mathrm{6}\boldsymbol{{xy}}+\mathrm{2}\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{x}}+\mathrm{3} \\ $$ $$=\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}{x}\right)^{\mathrm{2}} −\mathrm{2}×\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}{x}×\sqrt{\mathrm{2}}{y}+\left(\sqrt{\mathrm{2}}{y}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{1}+\left[\mathrm{7}−\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \right]{x}^{\mathrm{2}} +\left(\mathrm{3}−\mathrm{1}\right) \\ $$ $$=\left(\frac{\mathrm{3}}{\sqrt{\mathrm{2}}}{x}−\sqrt{\mathrm{2}}{y}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{2}}{x}+\mathrm{1}\right)^{\mathrm{2}} +\left(\frac{\mathrm{3}}{\mathrm{2}}{x}\right)^{\mathrm{2}} +\mathrm{2} \\ $$ $$>\mathrm{2}>\mathrm{0} \\ $$

Commented byMr Chheang Chantria last updated on 03/Apr/17

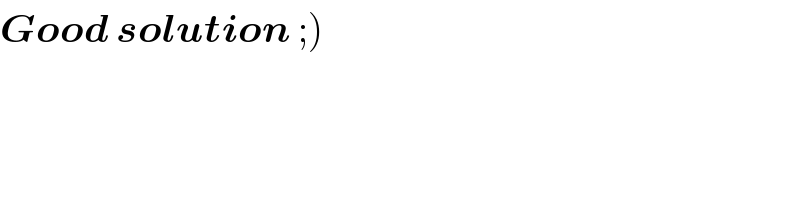
Good solution ;)

$$\left.\boldsymbol{{Good}}\:\boldsymbol{{solution}}\:;\right) \\ $$ $$ \\ $$

Answered by ajfour last updated on 02/Apr/17

6x^2 −6xy+2y^2 +x^2 +x+3 =2x^2 [3−((3y)/x)+((y/x))^2 ]+(x+(1/2))^2 −(1/4)+3 =2x^2 [((y/x)−(3/2))^2 −(9/4)+3 ]+(x+(1/2))^2 +((11)/4) =2x^2 [(((2y−3x)^2 )/(4x^2 ))+(3/4)]+(x+(1/2))^2 +((11)/4) =(((2y−3x)^2 )/2)+((3x^2 )/2)+(x+(1/2))^2 +((11)/4) >0

$$\mathrm{6}{x}^{\mathrm{2}} −\mathrm{6}{xy}+\mathrm{2}{y}^{\mathrm{2}} +{x}^{\mathrm{2}} +{x}+\mathrm{3} \\ $$ $$=\mathrm{2}{x}^{\mathrm{2}} \left[\mathrm{3}−\frac{\mathrm{3}{y}}{{x}}+\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \:\right]+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3} \\ $$ $$=\mathrm{2}{x}^{\mathrm{2}} \left[\left(\frac{{y}}{{x}}−\frac{\mathrm{3}}{\mathrm{2}}\right)^{\mathrm{2}} −\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{3}\:\right]+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}} \\ $$ $$=\mathrm{2}{x}^{\mathrm{2}} \left[\frac{\left(\mathrm{2}{y}−\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{4}{x}^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}}\right]+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}} \\ $$ $$=\frac{\left(\mathrm{2}{y}−\mathrm{3}{x}\right)^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{2}}+\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{11}}{\mathrm{4}}\:>\mathrm{0} \\ $$

Commented byMr Chheang Chantria last updated on 03/Apr/17

that′s so sweet ;)

$$\left.\boldsymbol{\mathrm{that}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{sweet}}\:;\right) \\ $$ $$ \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 02/Apr/17

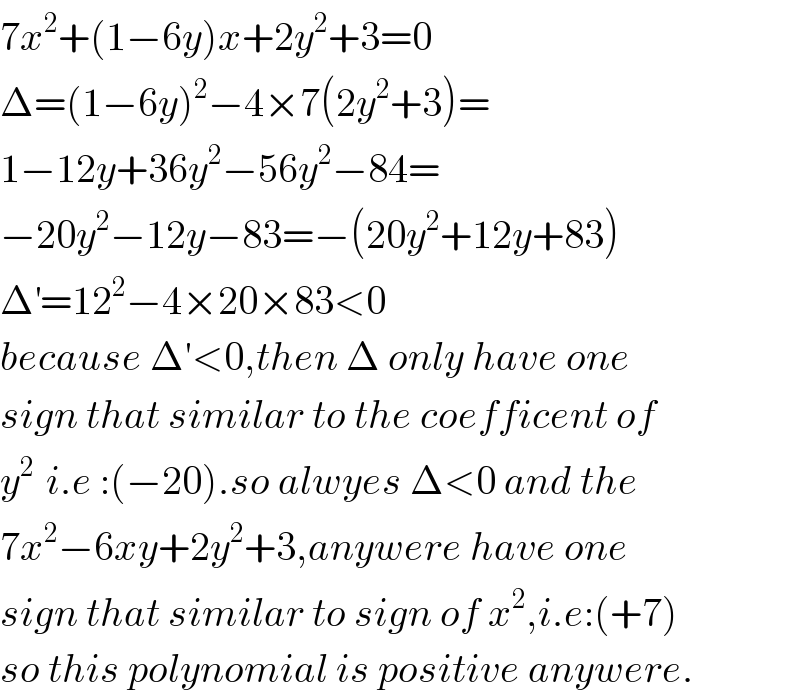
7x^2 +(1−6y)x+2y^2 +3=0 Δ=(1−6y)^2 −4×7(2y^2 +3)= 1−12y+36y^2 −56y^2 −84= −20y^2 −12y−83=−(20y^2 +12y+83) Δ^′ =12^2 −4×20×83<0 because Δ′<0,then Δ only have one sign that similar to the coefficent of y^(2 ) i.e :(−20).so alwyes Δ<0 and the 7x^2 −6xy+2y^2 +3,anywere have one sign that similar to sign of x^2 ,i.e:(+7) so this polynomial is positive anywere.

$$\mathrm{7}{x}^{\mathrm{2}} +\left(\mathrm{1}−\mathrm{6}{y}\right){x}+\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3}=\mathrm{0} \\ $$ $$\Delta=\left(\mathrm{1}−\mathrm{6}{y}\right)^{\mathrm{2}} −\mathrm{4}×\mathrm{7}\left(\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3}\right)= \\ $$ $$\mathrm{1}−\mathrm{12}{y}+\mathrm{36}{y}^{\mathrm{2}} −\mathrm{56}{y}^{\mathrm{2}} −\mathrm{84}= \\ $$ $$−\mathrm{20}{y}^{\mathrm{2}} −\mathrm{12}{y}−\mathrm{83}=−\left(\mathrm{20}{y}^{\mathrm{2}} +\mathrm{12}{y}+\mathrm{83}\right) \\ $$ $$\Delta^{'} =\mathrm{12}^{\mathrm{2}} −\mathrm{4}×\mathrm{20}×\mathrm{83}<\mathrm{0} \\ $$ $${because}\:\Delta'<\mathrm{0},{then}\:\Delta\:{only}\:{have}\:{one} \\ $$ $${sign}\:{that}\:{similar}\:{to}\:{the}\:{coefficent}\:{of} \\ $$ $${y}^{\mathrm{2}\:} \:{i}.{e}\::\left(−\mathrm{20}\right).{so}\:{alwyes}\:\Delta<\mathrm{0}\:{and}\:{the} \\ $$ $$\mathrm{7}{x}^{\mathrm{2}} −\mathrm{6}{xy}+\mathrm{2}{y}^{\mathrm{2}} +\mathrm{3},{anywere}\:{have}\:{one} \\ $$ $${sign}\:{that}\:{similar}\:{to}\:{sign}\:{of}\:{x}^{\mathrm{2}} ,{i}.{e}:\left(+\mathrm{7}\right) \\ $$ $${so}\:{this}\:{polynomial}\:{is}\:{positive}\:{anywere}. \\ $$

Commented bymrW1 last updated on 02/Apr/17

good and interesting point of view!

$${good}\:{and}\:{interesting}\:{point}\:{of}\:{view}! \\ $$

Commented byMr Chheang Chantria last updated on 03/Apr/17

nice solution and nice explain Thanks you ;)

$$\boldsymbol{{nice}}\:\boldsymbol{{solution}}\:\boldsymbol{{and}}\:\boldsymbol{{nice}}\:\boldsymbol{{explain}} \\ $$ $$\left.\boldsymbol{{Thanks}}\:\boldsymbol{{you}}\:;\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com