Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 118448 by peter frank last updated on 17/Oct/20

Answered by Olaf last updated on 17/Oct/20

A = π×7^2 −2∫_(−7) ^(+7) (7−(√(49−x^2 )))dx A = 49π−4∫_0 ^(+7) (7−(√(49−x^2 )))dx A = 49π−196+28∫_0 ^(+7) ((√(1−((x/7))^2 )))dx x = 7sinθ A = 49π−196+28∫_0 ^(π/2) (cosθ)×7cosθdθ A = 49π−196+196∫_0 ^(π/2) ((1+cos2θ)/2)dθ A = 49π−196+98[θ+((sin2θ)/2)]_0 ^(π/2) A = 49π−196+98((π/2)) A = 98π−196

$$\mathrm{A}\:=\:\pi×\mathrm{7}^{\mathrm{2}} −\mathrm{2}\int_{−\mathrm{7}} ^{+\mathrm{7}} \left(\mathrm{7}−\sqrt{\mathrm{49}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{4}\int_{\mathrm{0}} ^{+\mathrm{7}} \left(\mathrm{7}−\sqrt{\mathrm{49}−{x}^{\mathrm{2}} }\right){dx} \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{28}\int_{\mathrm{0}} ^{+\mathrm{7}} \left(\sqrt{\mathrm{1}−\left(\frac{{x}}{\mathrm{7}}\right)^{\mathrm{2}} }\right){dx} \\ $$$${x}\:=\:\mathrm{7sin}\theta \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{28}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{cos}\theta\right)×\mathrm{7cos}\theta{d}\theta \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{196}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}+\mathrm{cos2}\theta}{\mathrm{2}}{d}\theta \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{98}\left[\theta+\frac{\mathrm{sin2}\theta}{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\mathrm{A}\:=\:\mathrm{49}\pi−\mathrm{196}+\mathrm{98}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\mathrm{A}\:=\:\mathrm{98}\pi−\mathrm{196} \\ $$

Commented by peter frank last updated on 17/Oct/20

ans 33.6 cm^2

$$\mathrm{ans}\:\mathrm{33}.\mathrm{6}\:\mathrm{cm}^{\mathrm{2}} \\ $$

Answered by mr W last updated on 18/Oct/20

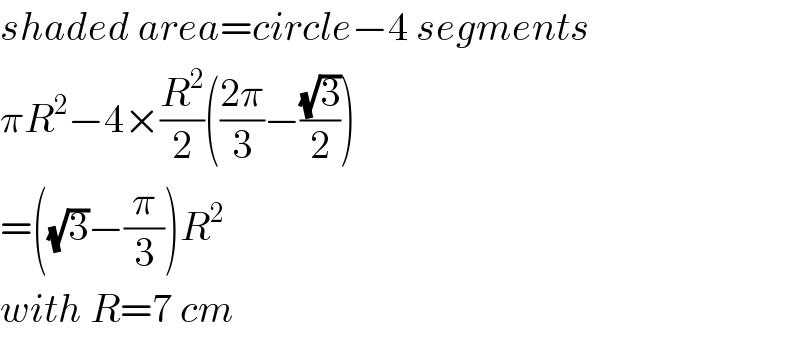
shaded area=circle−4 segments πR^2 −4×(R^2 /2)(((2π)/3)−((√3)/2)) =((√3)−(π/3))R^2 with R=7 cm

$${shaded}\:{area}={circle}−\mathrm{4}\:{segments} \\ $$$$\pi{R}^{\mathrm{2}} −\mathrm{4}×\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$=\left(\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{3}}\right){R}^{\mathrm{2}} \\ $$$${with}\:{R}=\mathrm{7}\:{cm} \\ $$

Commented by peter frank last updated on 17/Oct/20

ans 33.6cm^2

$$\mathrm{ans}\:\mathrm{33}.\mathrm{6cm}^{\mathrm{2}} \\ $$

Commented by mr W last updated on 18/Oct/20

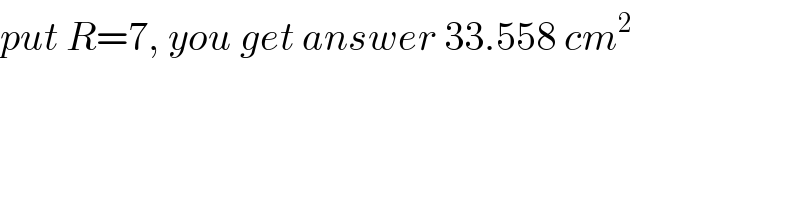
put R=7, you get answer 33.558 cm^2

$${put}\:{R}=\mathrm{7},\:{you}\:{get}\:{answer}\:\mathrm{33}.\mathrm{558}\:{cm}^{\mathrm{2}} \\ $$

Commented by mr W last updated on 18/Oct/20

it is meant that the radius of circle is equal the radius of segment. the diagram was just not well made.

$${it}\:{is}\:{meant}\:{that}\:{the}\:{radius}\:{of}\:{circle} \\ $$$${is}\:{equal}\:{the}\:{radius}\:{of}\:{segment}. \\ $$$${the}\:{diagram}\:{was}\:{just}\:{not}\:{well}\:{made}. \\ $$

Commented by peter frank last updated on 18/Oct/20

more explanation.i did not understood (((2π)/3)−((√3)/2)) ?

$$\mathrm{more}\:\mathrm{explanation}.\mathrm{i}\:\mathrm{did} \\ $$$$\mathrm{not}\:\mathrm{understood} \\ $$$$\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:? \\ $$

Commented by mr W last updated on 18/Oct/20

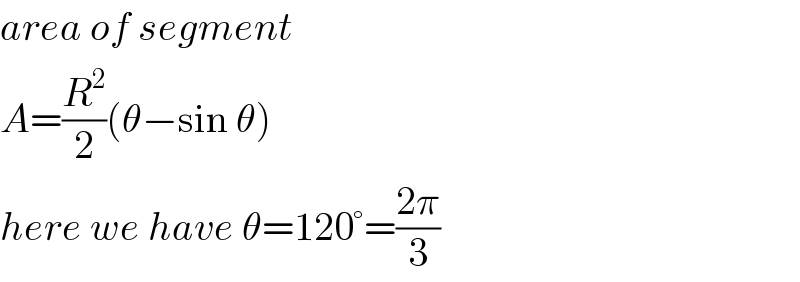
area of segment A=(R^2 /2)(θ−sin θ) here we have θ=120°=((2π)/3)

$${area}\:{of}\:{segment} \\ $$$${A}=\frac{{R}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right) \\ $$$${here}\:{we}\:{have}\:\theta=\mathrm{120}°=\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$

Commented by mr W last updated on 18/Oct/20

Commented by mr W last updated on 18/Oct/20

Commented by 1549442205PVT last updated on 18/Oct/20

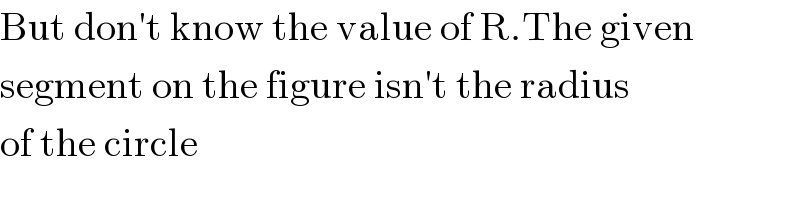
But don′t know the value of R.The given segment on the figure isn′t the radius of the circle

$$\mathrm{But}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{R}.\mathrm{The}\:\mathrm{given} \\ $$$$\mathrm{segment}\:\mathrm{on}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{isn}'\mathrm{t}\:\mathrm{the}\:\mathrm{radius} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{circle} \\ $$

Commented by mr W last updated on 18/Oct/20

Commented by peter frank last updated on 18/Oct/20

Commented by peter frank last updated on 18/Oct/20

i think this diagram clear

$$\mathrm{i}\:\mathrm{think}\:\mathrm{this}\:\mathrm{diagram} \\ $$$$\mathrm{clear} \\ $$

Commented by peter frank last updated on 18/Oct/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by 1549442205PVT last updated on 18/Oct/20

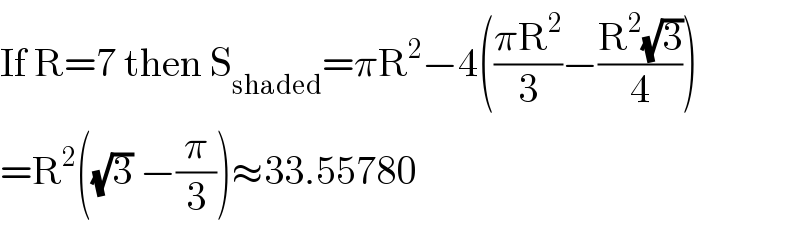
If R=7 then S_(shaded) =πR^2 −4(((πR^2 )/3)−((R^2 (√3))/4)) =R^2 ((√3) −(π/3))≈33.55780

$$\mathrm{If}\:\mathrm{R}=\mathrm{7}\:\mathrm{then}\:\mathrm{S}_{\mathrm{shaded}} =\pi\mathrm{R}^{\mathrm{2}} −\mathrm{4}\left(\frac{\pi\mathrm{R}^{\mathrm{2}} }{\mathrm{3}}−\frac{\mathrm{R}^{\mathrm{2}} \sqrt{\mathrm{3}}}{\mathrm{4}}\right) \\ $$$$=\mathrm{R}^{\mathrm{2}} \left(\sqrt{\mathrm{3}}\:−\frac{\pi}{\mathrm{3}}\right)\approx\mathrm{33}.\mathrm{55780} \\ $$

Commented by peter frank last updated on 18/Oct/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Answered by 1549442205PVT last updated on 18/Oct/20

Commented by 1549442205PVT last updated on 18/Oct/20

This problem doesn′t have enough data to solve.Indeed,we prove that can construct many the figures satisfying the condition of problem Put α=ASQ^(�) ,R−the radius of the circles with the centers at (A) and (C).Then AQ=2Rsinα,AO=R.Hence,from the hypothesis we have PQ⊥SN at A and NP=OQ=7.From Pithagorean′s theorem we have:AQ^2 +AO^2 =OQ^2 =49 ⇔4R^2 sin^2 α+R^2 =49⇒R=(7/( (√(4sin^2 α+1)))) or sinα=(√((49−R^2 )/(4R^2 )))=((√(49−R^2 ))/(2R)) Therefore,for each of valuesR satisfying 4.95≈(7/( (√2)))≤R<7 we determine one value of the angle α as on the figure and the segments NP=OQ=7 satisfying the cionditions of given problem!

$$\mathrm{This}\:\mathrm{problem}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{have}\:\mathrm{enough}\: \\ $$$$\mathrm{data}\:\mathrm{to}\:\mathrm{solve}.\mathrm{Indeed},\mathrm{we}\:\:\mathrm{prove} \\ $$$$\mathrm{that}\:\mathrm{can}\:\mathrm{construct}\:\mathrm{many}\:\mathrm{the}\:\mathrm{figures} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{of}\:\mathrm{problem} \\ $$$$\mathrm{Put}\:\alpha=\widehat {\mathrm{ASQ}},\mathrm{R}−\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{circles} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{centers}\:\mathrm{at}\:\left(\mathrm{A}\right)\:\mathrm{and}\:\left(\mathrm{C}\right).\mathrm{Then} \\ $$$$\mathrm{AQ}=\mathrm{2Rsin}\alpha,\mathrm{AO}=\mathrm{R}.\mathrm{Hence},\mathrm{from}\:\mathrm{the} \\ $$$$\mathrm{hypothesis}\:\mathrm{we}\:\mathrm{have}\:\mathrm{PQ}\bot\mathrm{SN}\:\mathrm{at}\:\mathrm{A}\:\mathrm{and} \\ $$$$\mathrm{NP}=\mathrm{OQ}=\mathrm{7}.\mathrm{From}\:\mathrm{Pithagorean}'\mathrm{s} \\ $$$$\mathrm{theorem}\:\mathrm{we}\:\mathrm{have}:\mathrm{AQ}^{\mathrm{2}} +\mathrm{AO}^{\mathrm{2}} =\mathrm{OQ}^{\mathrm{2}} =\mathrm{49} \\ $$$$\Leftrightarrow\mathrm{4R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \alpha+\mathrm{R}^{\mathrm{2}} =\mathrm{49}\Rightarrow\mathrm{R}=\frac{\mathrm{7}}{\:\sqrt{\mathrm{4sin}^{\mathrm{2}} \alpha+\mathrm{1}}} \\ $$$$\mathrm{or}\:\mathrm{sin}\alpha=\sqrt{\frac{\mathrm{49}−\mathrm{R}^{\mathrm{2}} }{\mathrm{4R}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{49}−\mathrm{R}^{\mathrm{2}} }}{\mathrm{2R}} \\ $$$$\mathrm{Therefore},\mathrm{for}\:\mathrm{each}\:\mathrm{of}\:\mathrm{valuesR}\:\mathrm{satisfying} \\ $$$$\mathrm{4}.\mathrm{95}\approx\frac{\mathrm{7}}{\:\sqrt{\mathrm{2}}}\leqslant\mathrm{R}<\mathrm{7}\:\mathrm{we}\:\mathrm{determine}\:\mathrm{one}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{angle}\:\alpha\:\mathrm{as}\:\mathrm{on}\:\mathrm{the}\:\mathrm{figure}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{segments}\:\mathrm{NP}=\mathrm{OQ}=\mathrm{7}\:\mathrm{satisfying}\:\mathrm{the}\: \\ $$$$\mathrm{cionditions}\:\mathrm{of}\:\mathrm{given}\:\mathrm{problem}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com