Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 118452 by 2004 last updated on 17/Oct/20

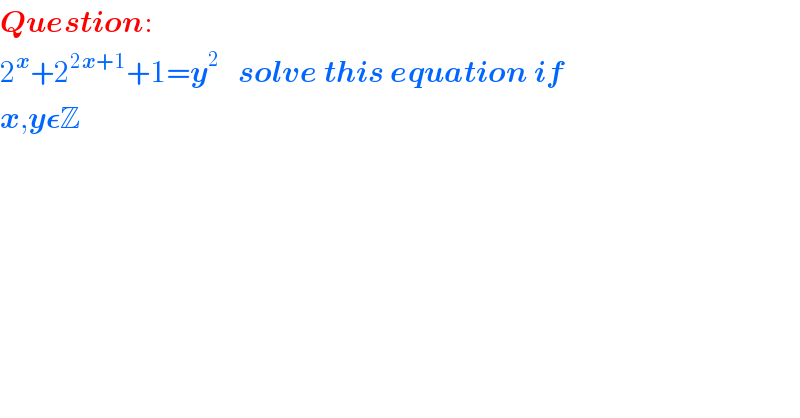
Question: 2^x +2^(2x+1) +1=y^2 solve this equation if x,y𝛆Z

$$\boldsymbol{{Question}}: \\ $$$$\mathrm{2}^{\boldsymbol{{x}}} +\mathrm{2}^{\mathrm{2}\boldsymbol{{x}}+\mathrm{1}} +\mathrm{1}=\boldsymbol{{y}}^{\mathrm{2}} \:\:\:\boldsymbol{{solve}}\:\boldsymbol{{this}}\:\boldsymbol{{equation}}\:\boldsymbol{{if}} \\ $$$$\boldsymbol{{x}},\boldsymbol{{y}\epsilon}\mathbb{Z} \\ $$

Commented by prakash jain last updated on 18/Oct/20

2^x +2^(2x+1) +1=y^2 x=0,y=Β±2 is obvious solution x>0 LHS is odd x=1 has no solution. xβ‰₯2 y=2k+1 2^x +2^(2x+1) =4k^2 +4k k(k+1)=2^(2xβˆ’1) +2^(xβˆ’2) =2^(xβˆ’2) (2^(x+1) +1) will continue

$$\mathrm{2}^{{x}} +\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} +\mathrm{1}={y}^{\mathrm{2}} \\ $$$${x}=\mathrm{0},{y}=\pm\mathrm{2}\:\mathrm{is}\:\mathrm{obvious}\:\mathrm{solution} \\ $$$${x}>\mathrm{0}\:\mathrm{LHS}\:\mathrm{is}\:\mathrm{odd} \\ $$$${x}=\mathrm{1}\:\mathrm{has}\:\mathrm{no}\:\mathrm{solution}. \\ $$$${x}\geqslant\mathrm{2} \\ $$$${y}=\mathrm{2}{k}+\mathrm{1} \\ $$$$\mathrm{2}^{{x}} +\mathrm{2}^{\mathrm{2}{x}+\mathrm{1}} =\mathrm{4}{k}^{\mathrm{2}} +\mathrm{4}{k} \\ $$$${k}\left({k}+\mathrm{1}\right)=\mathrm{2}^{\mathrm{2}{x}βˆ’\mathrm{1}} +\mathrm{2}^{{x}βˆ’\mathrm{2}} =\mathrm{2}^{{x}βˆ’\mathrm{2}} \left(\mathrm{2}^{{x}+\mathrm{1}} +\mathrm{1}\right) \\ $$$${will}\:{continue} \\ $$

Commented by 2004 last updated on 18/Oct/20

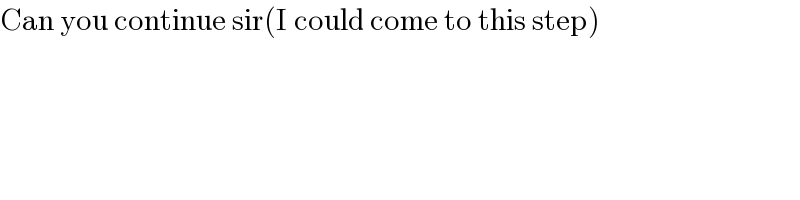
Can you continue sir(I could come to this step)

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{continue}\:\mathrm{sir}\left(\mathrm{I}\:\mathrm{could}\:\mathrm{come}\:\mathrm{to}\:\mathrm{this}\:\mathrm{step}\right) \\ $$

Commented by 2004 last updated on 18/Oct/20

Thanks

$$\boldsymbol{{Thanks}} \\ $$

Answered by floor(10Β²Eta[1]) last updated on 18/Oct/20

if x<0β‡’xβ‰€βˆ’1 β‡’2^x ≀(1/2), 2^(2x+1) ≀(1/2) 1<1+2^x +2^(2x+1) ≀1+(1/2)+(1/2)=2 β‡’1<y^2 ≀2β‡’no solution for x<0. if x=0: β‡’1+2^x +2^(2x+1) =4=y^2 β‡’y=Β±2 (x, y)={(0, βˆ’2), (0, 2)} if x=1: β‡’1+2+2^3 =11=y^2 β‡’no sol. x=2: 1+2^2 +2^5 =37=y^2 β‡’no sol. Suppose xβ‰₯3: 1+2^x +2^(2x+1) =y^2 2^x +2^(2x+1) =y^2 βˆ’1=(y+1)(y+1) 2^x (1+2^(x+1) )=(y+1)(yβˆ’1) LHS is evenβ‡’RHS is also even but y+1 and yβˆ’1 have the same parity β‡’y+1 and yβˆ’1 are even β‡’gcd(y+1,yβˆ’1)∣2 β‡’gcd(y+1,yβˆ’1)=2 β‡’y+1 or yβˆ’1 is divisible by 2 but not a larger power of 2 like 4 (y+1)(yβˆ’1)=2.2^(xβˆ’1) (1+2^(x+1) ) so y+1 or yβˆ’1 is a multiple of 2^(xβˆ’1) Case 1: y+1=2^(xβˆ’1) .m (mβ‰₯1, odd) (If m was even then that would imply that yβˆ’1 was odd because y+1 would take all of the even part of the RHS, but we know that they are both even. And mβ‰₯1 because if (x,y) is a sol. so is (x, βˆ’y), so we only need to look for yβ‰₯0) β‡’y=2^(xβˆ’1) .mβˆ’1 1+2^x +2^(2x+1) =(2^(xβˆ’1) .mβˆ’1)^2 =2^(2xβˆ’2) .m^2 βˆ’2^x .m+1 β‡’1+2^(x+1) =2^(xβˆ’2) .m^2 βˆ’m m+1=2^(xβˆ’2) .m^2 βˆ’2^(x+1) =2^(xβˆ’2) (m^2 βˆ’8) m+1=2^(xβˆ’2) (m^2 βˆ’8)β‰₯2(m^2 βˆ’8) 2m^2 βˆ’mβˆ’17≀0 ((1βˆ’(√(137)))/2)≀m≀((1+(√(137)))/2) but since mβ‰₯1: 1≀m≀((1+(√(137)))/4)<4β‡’m=1 or m=3 m=1β‡’2=2^(xβˆ’2) (βˆ’7) (no sol.) m=3β‡’4=2^(xβˆ’2) β‡’x=4 1+2^4 +2^9 =y^2 β‡’y=Β±23 Case 2: yβˆ’1=2^(xβˆ’1) .m (mβ‰₯1, odd) y=2^(xβˆ’1) .m+1 1+2^x +2^(2x+1) =(2^(xβˆ’1) .m+1)^2 =2^(2xβˆ’2) .m^2 +2^x .m+1 1+2^(x+1) =2^(xβˆ’2) .m^2 +m 1βˆ’m=2^(xβˆ’2) .m^2 βˆ’2^(x+1) =2^(xβˆ’2) (m^2 βˆ’8) 0β‰₯1βˆ’m=2^(xβˆ’1) (m^2 βˆ’8) β‡’m^2 βˆ’8≀0β‡’m=1 (doesnβ€²t work) all the solutions are: (x, y)=(0, βˆ’2), (0, 2), (4, βˆ’23), (4, 23)

$$\mathrm{if}\:\mathrm{x}<\mathrm{0}\Rightarrow\mathrm{x}\leqslantβˆ’\mathrm{1} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{x}} \leqslant\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{2}^{\mathrm{2x}+\mathrm{1}} \leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{1}<\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} \leqslant\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{1}<\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{2}\Rightarrow\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:\mathrm{x}<\mathrm{0}. \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{0}: \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\mathrm{4}=\mathrm{y}^{\mathrm{2}} \Rightarrow\mathrm{y}=\pm\mathrm{2} \\ $$$$\left(\mathrm{x},\:\mathrm{y}\right)=\left\{\left(\mathrm{0},\:βˆ’\mathrm{2}\right),\:\left(\mathrm{0},\:\mathrm{2}\right)\right\} \\ $$$$\mathrm{if}\:\mathrm{x}=\mathrm{1}: \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}+\mathrm{2}^{\mathrm{3}} =\mathrm{11}=\mathrm{y}^{\mathrm{2}} \Rightarrow\mathrm{no}\:\mathrm{sol}. \\ $$$$\mathrm{x}=\mathrm{2}: \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{5}} =\mathrm{37}=\mathrm{y}^{\mathrm{2}} \Rightarrow\mathrm{no}\:\mathrm{sol}. \\ $$$$\mathrm{Suppose}\:\mathrm{x}\geqslant\mathrm{3}: \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\mathrm{y}^{\mathrm{2}} βˆ’\mathrm{1}=\left(\mathrm{y}+\mathrm{1}\right)\left(\mathrm{y}+\mathrm{1}\right) \\ $$$$\mathrm{2}^{\mathrm{x}} \left(\mathrm{1}+\mathrm{2}^{\mathrm{x}+\mathrm{1}} \right)=\left(\mathrm{y}+\mathrm{1}\right)\left(\mathrm{y}βˆ’\mathrm{1}\right) \\ $$$$\mathrm{LHS}\:\mathrm{is}\:\mathrm{even}\Rightarrow\mathrm{RHS}\:\mathrm{is}\:\mathrm{also}\:\mathrm{even}\:\mathrm{but} \\ $$$$\mathrm{y}+\mathrm{1}\:\mathrm{and}\:\mathrm{y}βˆ’\mathrm{1}\:\mathrm{have}\:\mathrm{the}\:\mathrm{same}\:\mathrm{parity} \\ $$$$\Rightarrow\mathrm{y}+\mathrm{1}\:\mathrm{and}\:\mathrm{y}βˆ’\mathrm{1}\:\mathrm{are}\:\mathrm{even} \\ $$$$\Rightarrow\mathrm{gcd}\left(\mathrm{y}+\mathrm{1},\mathrm{y}βˆ’\mathrm{1}\right)\mid\mathrm{2} \\ $$$$\Rightarrow\mathrm{gcd}\left(\mathrm{y}+\mathrm{1},\mathrm{y}βˆ’\mathrm{1}\right)=\mathrm{2} \\ $$$$\Rightarrow\mathrm{y}+\mathrm{1}\:\mathrm{or}\:\mathrm{y}βˆ’\mathrm{1}\:\mathrm{is}\:\mathrm{divisible}\:\mathrm{by}\:\mathrm{2}\:\mathrm{but}\:\mathrm{not}\:\mathrm{a}\: \\ $$$$\mathrm{larger}\:\mathrm{power}\:\mathrm{of}\:\mathrm{2}\:\mathrm{like}\:\mathrm{4} \\ $$$$\left(\mathrm{y}+\mathrm{1}\right)\left(\mathrm{y}βˆ’\mathrm{1}\right)=\mathrm{2}.\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} \left(\mathrm{1}+\mathrm{2}^{\mathrm{x}+\mathrm{1}} \right) \\ $$$$\mathrm{so}\:\mathrm{y}+\mathrm{1}\:\mathrm{or}\:\mathrm{y}βˆ’\mathrm{1}\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} \\ $$$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{y}+\mathrm{1}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}\:\left(\mathrm{m}\geqslant\mathrm{1},\:\mathrm{odd}\right) \\ $$$$\left(\mathrm{If}\:\mathrm{m}\:\mathrm{was}\:\mathrm{even}\:\mathrm{then}\:\mathrm{that}\:\mathrm{would}\:\mathrm{imply}\right. \\ $$$$\mathrm{that}\:\mathrm{y}βˆ’\mathrm{1}\:\mathrm{was}\:\mathrm{odd}\:\mathrm{because}\:\mathrm{y}+\mathrm{1}\:\mathrm{would}\:\mathrm{take} \\ $$$$\mathrm{all}\:\mathrm{of}\:\mathrm{the}\:\mathrm{even}\:\mathrm{part}\:\mathrm{of}\:\mathrm{the}\:\mathrm{RHS},\:\mathrm{but}\: \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that}\:\mathrm{they}\:\mathrm{are}\:\mathrm{both}\:\mathrm{even}.\: \\ $$$$\mathrm{And}\:\mathrm{m}\geqslant\mathrm{1}\:\mathrm{because}\:\mathrm{if}\:\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{sol}.\:\mathrm{so}\:\mathrm{is} \\ $$$$\left.\left(\mathrm{x},\:βˆ’\mathrm{y}\right),\:\mathrm{so}\:\mathrm{we}\:\mathrm{only}\:\mathrm{need}\:\mathrm{to}\:\mathrm{look}\:\mathrm{for}\:\mathrm{y}\geqslant\mathrm{0}\right) \\ $$$$\Rightarrow\mathrm{y}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}βˆ’\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\left(\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}βˆ’\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2x}βˆ’\mathrm{2}} .\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{2}^{\mathrm{x}} .\mathrm{m}+\mathrm{1} \\ $$$$\Rightarrow\mathrm{1}+\mathrm{2}^{\mathrm{x}+\mathrm{1}} =\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} .\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{m} \\ $$$$\mathrm{m}+\mathrm{1}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} .\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{2}^{\mathrm{x}+\mathrm{1}} =\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} \left(\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{8}\right) \\ $$$$\mathrm{m}+\mathrm{1}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} \left(\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{8}\right)\geqslant\mathrm{2}\left(\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{8}\right) \\ $$$$\mathrm{2m}^{\mathrm{2}} βˆ’\mathrm{m}βˆ’\mathrm{17}\leqslant\mathrm{0} \\ $$$$\frac{\mathrm{1}βˆ’\sqrt{\mathrm{137}}}{\mathrm{2}}\leqslant\mathrm{m}\leqslant\frac{\mathrm{1}+\sqrt{\mathrm{137}}}{\mathrm{2}} \\ $$$$\mathrm{but}\:\mathrm{since}\:\mathrm{m}\geqslant\mathrm{1}: \\ $$$$\mathrm{1}\leqslant\mathrm{m}\leqslant\frac{\mathrm{1}+\sqrt{\mathrm{137}}}{\mathrm{4}}<\mathrm{4}\Rightarrow\mathrm{m}=\mathrm{1}\:\mathrm{or}\:\mathrm{m}=\mathrm{3} \\ $$$$\mathrm{m}=\mathrm{1}\Rightarrow\mathrm{2}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} \left(βˆ’\mathrm{7}\right)\:\left(\mathrm{no}\:\mathrm{sol}.\right) \\ $$$$\mathrm{m}=\mathrm{3}\Rightarrow\mathrm{4}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} \Rightarrow\mathrm{x}=\mathrm{4} \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{4}} +\mathrm{2}^{\mathrm{9}} =\mathrm{y}^{\mathrm{2}} \Rightarrow\mathrm{y}=\pm\mathrm{23} \\ $$$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{y}βˆ’\mathrm{1}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}\:\left(\mathrm{m}\geqslant\mathrm{1},\:\mathrm{odd}\right) \\ $$$$\mathrm{y}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{x}} +\mathrm{2}^{\mathrm{2x}+\mathrm{1}} =\left(\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{2}^{\mathrm{2x}βˆ’\mathrm{2}} .\mathrm{m}^{\mathrm{2}} +\mathrm{2}^{\mathrm{x}} .\mathrm{m}+\mathrm{1} \\ $$$$\mathrm{1}+\mathrm{2}^{\mathrm{x}+\mathrm{1}} =\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} .\mathrm{m}^{\mathrm{2}} +\mathrm{m} \\ $$$$\mathrm{1}βˆ’\mathrm{m}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} .\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{2}^{\mathrm{x}+\mathrm{1}} =\mathrm{2}^{\mathrm{x}βˆ’\mathrm{2}} \left(\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{8}\right) \\ $$$$\mathrm{0}\geqslant\mathrm{1}βˆ’\mathrm{m}=\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} \left(\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{8}\right) \\ $$$$\Rightarrow\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{8}\leqslant\mathrm{0}\Rightarrow\mathrm{m}=\mathrm{1}\:\left(\mathrm{doesn}'\mathrm{t}\:\mathrm{work}\right) \\ $$$$\mathrm{all}\:\mathrm{the}\:\mathrm{solutions}\:\mathrm{are}: \\ $$$$\left(\mathrm{x},\:\mathrm{y}\right)=\left(\mathrm{0},\:βˆ’\mathrm{2}\right),\:\left(\mathrm{0},\:\mathrm{2}\right),\:\left(\mathrm{4},\:βˆ’\mathrm{23}\right),\:\left(\mathrm{4},\:\mathrm{23}\right) \\ $$

Commented by 1549442205PVT last updated on 18/Oct/20

If so such then 1+2^x =2^(xβˆ’3) .m^2 βˆ’m your argument later still true.You can go by path base on system { ((2^(xβˆ’1) .m=y+1)),((((2.(2^(x+1) +1))/m)=yβˆ’1)) :} Thank you

$$\mathrm{If}\:\mathrm{so}\:\mathrm{such}\:\mathrm{then}\:\mathrm{1}+\mathrm{2}^{\mathrm{x}} =\mathrm{2}^{\mathrm{x}βˆ’\mathrm{3}} .\mathrm{m}^{\mathrm{2}} βˆ’\mathrm{m} \\ $$$$\mathrm{your}\:\mathrm{argument}\:\mathrm{later}\:\mathrm{still}\:\mathrm{true}.\mathrm{You} \\ $$$$\mathrm{can}\:\mathrm{go}\:\mathrm{by}\:\mathrm{path}\:\mathrm{base}\:\mathrm{on}\:\mathrm{system} \\ $$$$\begin{cases}{\mathrm{2}^{\mathrm{x}βˆ’\mathrm{1}} .\mathrm{m}=\mathrm{y}+\mathrm{1}}\\{\frac{\mathrm{2}.\left(\mathrm{2}^{\mathrm{x}+\mathrm{1}} +\mathrm{1}\right)}{\mathrm{m}}=\mathrm{y}βˆ’\mathrm{1}}\end{cases} \\ $$$$\mathrm{Thank}\:\mathrm{you} \\ $$

Answered by TANMAY PANACEA last updated on 18/Oct/20

by inspection x=0 y=2

$$\boldsymbol{{by}}\:\boldsymbol{{inspection}} \\ $$$$\boldsymbol{{x}}=\mathrm{0}\:\:\:\boldsymbol{{y}}=\mathrm{2} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com