
Question and Answers Forum
Question Number 118466 by mathdave last updated on 17/Oct/20
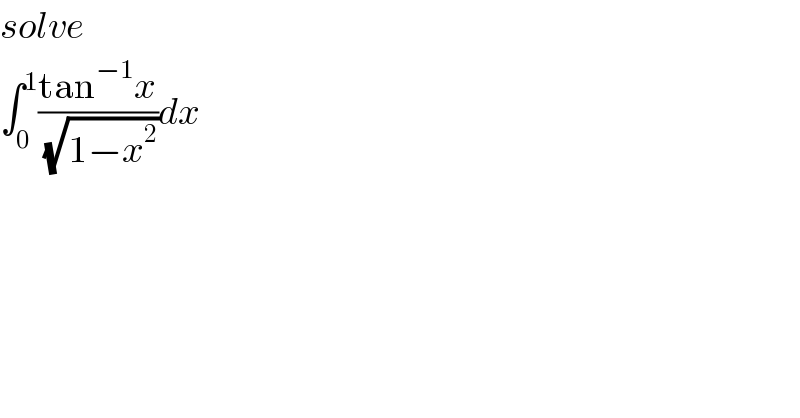
Answered by mathmax by abdo last updated on 17/Oct/20
![let take a try with series I =∫_0 ^1 ((arctanx)/(√(1−x^2 )))dx changement x=sint give I =∫_0 ^(π/2) ((arctan(sint))/(cost))cost dt =∫_0 ^(π/2) arctan(sint)dt =[t arctan(sint)]_0 ^(π/2) −∫_0 ^(π/2) t .((cost)/(1+sin^2 t))dt =(π^2 /8)−∫_0 ^(π/2) ((t cost)/(1+sin^2 t))dt chang. tan((t/2))=u give ∫_0 ^(π/2) ((t cost)/(1+sin^2 t))dt =∫_0 ^1 ((2 arctanu×((1−u^2 )/(1+u^2 )))/(1+((4u^2 )/(1+u^2 ))))×((2du)/(1+u^2 )) =4 ∫_0 ^1 (((1−u^2 )arctanu)/((1+u^2 )( 1+u^2 +4u^2 )))du =4 ∫_0 ^1 (((1−u^2 )arctanu)/((u^2 +1)(5u^2 +1)))du =(4/5)×((−5)/4)∫_0 ^1 (1−u^2 )arctanu{(1/(u^2 +1))−(1/(u^2 +(1/5)))}du =∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du−∫_0 ^1 (((u^2 −1)arctanu)/(u^2 +(1/5)))du ∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du =∫_0 ^1 (u^2 −1)arctanu(Σ_(n=0) ^∞ (−1)^n u^(2n) )du =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 (u^(2n+2) −u^(2n) )arctanu du =Σ_(n=0) ^∞ (−1)^n U_n U_n =∫_0 ^1 (u^(2n+2) −u^(2n) )arctanu du=[((u^(2n+3) /(2n+3))−(u^(2n+1) /(2n+1)))arctanu]_0 ^1 −∫_0 ^1 ((u^(2n+3) /(2n+3))−(u^(2n+1) /(2n+1)))(du/(1+u^2 )) =(π/4)((1/(2n+3))−(1/(2n+1))) +(1/(2n+1))∫_0 ^1 (u^(2n+1) /(1+u^2 ))du−(1/(2n+3))∫_0 ^1 (u^(2n+3) /(1+u^2 ))du also ∫_0 ^1 (u^(2n+1) /(1+u^2 ))du =∫_0 ^1 u^(2n+1) Σ_(p=0) ^∞ (−1)^p u^(2p) =Σ_(p=0) ^∞ (−1)^p ∫_0 ^1 u^(2n+2p+1) =Σ_(p=0) ^∞ (((−1)^p )/(2n+2p+2)) and ∫_0 ^1 (u^(2n+3) /(1+u^2 ))du =Σ_(p=0) ^∞ (((−1)^p )/(2n+2p +4)) ⇒ U_n =(π/4)((1/(2n+3))−(1/(2n+1)))+(1/(2(2n+1)))Σ_(p=0) ^∞ (((−1)^p )/(n+p+1)) −(1/(2(2n+3)))Σ_(p=0) ^∞ (((−1)^p )/(n+p+2)) ⇒ ∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du =(π/4)Σ_(n=0) ^∞ (((−1)^n )/(2n+3))−(π/4)Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) +(1/2)Σ_(n=0) ^∞ (Σ_(p=0) ^∞ (((−1)^p )/((2n+1)(n+p+1))))−(1/2)Σ_(n=0) ^∞ (Σ_(p=0) ^∞ (((−1)^p )/((2n+3)(n+p+2)))) ...be continued...](Q118472.png)
Answered by TANMAY PANACEA last updated on 17/Oct/20

| ||
Question and Answers Forum | ||
Question Number 118466 by mathdave last updated on 17/Oct/20 | ||
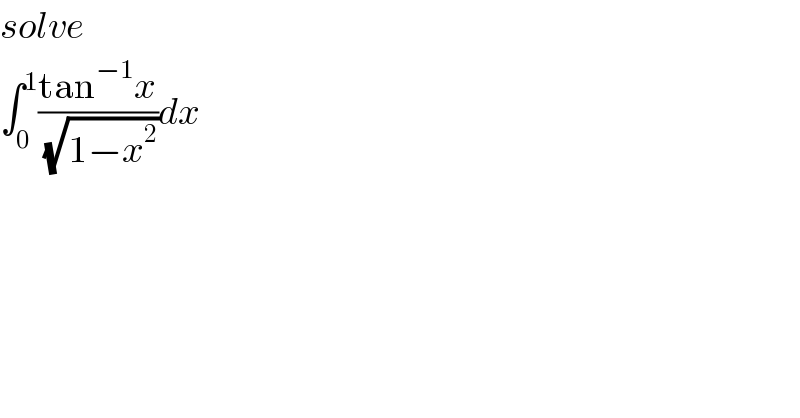 | ||
Answered by mathmax by abdo last updated on 17/Oct/20 | ||
![let take a try with series I =∫_0 ^1 ((arctanx)/(√(1−x^2 )))dx changement x=sint give I =∫_0 ^(π/2) ((arctan(sint))/(cost))cost dt =∫_0 ^(π/2) arctan(sint)dt =[t arctan(sint)]_0 ^(π/2) −∫_0 ^(π/2) t .((cost)/(1+sin^2 t))dt =(π^2 /8)−∫_0 ^(π/2) ((t cost)/(1+sin^2 t))dt chang. tan((t/2))=u give ∫_0 ^(π/2) ((t cost)/(1+sin^2 t))dt =∫_0 ^1 ((2 arctanu×((1−u^2 )/(1+u^2 )))/(1+((4u^2 )/(1+u^2 ))))×((2du)/(1+u^2 )) =4 ∫_0 ^1 (((1−u^2 )arctanu)/((1+u^2 )( 1+u^2 +4u^2 )))du =4 ∫_0 ^1 (((1−u^2 )arctanu)/((u^2 +1)(5u^2 +1)))du =(4/5)×((−5)/4)∫_0 ^1 (1−u^2 )arctanu{(1/(u^2 +1))−(1/(u^2 +(1/5)))}du =∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du−∫_0 ^1 (((u^2 −1)arctanu)/(u^2 +(1/5)))du ∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du =∫_0 ^1 (u^2 −1)arctanu(Σ_(n=0) ^∞ (−1)^n u^(2n) )du =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 (u^(2n+2) −u^(2n) )arctanu du =Σ_(n=0) ^∞ (−1)^n U_n U_n =∫_0 ^1 (u^(2n+2) −u^(2n) )arctanu du=[((u^(2n+3) /(2n+3))−(u^(2n+1) /(2n+1)))arctanu]_0 ^1 −∫_0 ^1 ((u^(2n+3) /(2n+3))−(u^(2n+1) /(2n+1)))(du/(1+u^2 )) =(π/4)((1/(2n+3))−(1/(2n+1))) +(1/(2n+1))∫_0 ^1 (u^(2n+1) /(1+u^2 ))du−(1/(2n+3))∫_0 ^1 (u^(2n+3) /(1+u^2 ))du also ∫_0 ^1 (u^(2n+1) /(1+u^2 ))du =∫_0 ^1 u^(2n+1) Σ_(p=0) ^∞ (−1)^p u^(2p) =Σ_(p=0) ^∞ (−1)^p ∫_0 ^1 u^(2n+2p+1) =Σ_(p=0) ^∞ (((−1)^p )/(2n+2p+2)) and ∫_0 ^1 (u^(2n+3) /(1+u^2 ))du =Σ_(p=0) ^∞ (((−1)^p )/(2n+2p +4)) ⇒ U_n =(π/4)((1/(2n+3))−(1/(2n+1)))+(1/(2(2n+1)))Σ_(p=0) ^∞ (((−1)^p )/(n+p+1)) −(1/(2(2n+3)))Σ_(p=0) ^∞ (((−1)^p )/(n+p+2)) ⇒ ∫_0 ^1 (((u^2 −1)arctanu)/(1+u^2 ))du =(π/4)Σ_(n=0) ^∞ (((−1)^n )/(2n+3))−(π/4)Σ_(n=0) ^∞ (((−1)^n )/(2n+1)) +(1/2)Σ_(n=0) ^∞ (Σ_(p=0) ^∞ (((−1)^p )/((2n+1)(n+p+1))))−(1/2)Σ_(n=0) ^∞ (Σ_(p=0) ^∞ (((−1)^p )/((2n+3)(n+p+2)))) ...be continued...](Q118472.png) | ||
| ||
Answered by TANMAY PANACEA last updated on 17/Oct/20 | ||
 | ||
| ||