
Question and Answers Forum
Question Number 118485 by bramlexs22 last updated on 18/Oct/20
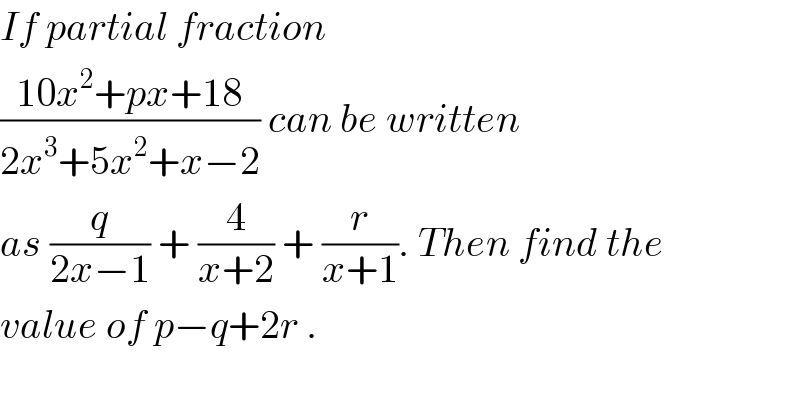
Answered by benjo_mathlover last updated on 18/Oct/20
![⇒ ((10x^2 +px+18)/(2x^3 +5x^2 +x−2)) ≡ (q/(2x−1)) + (4/(x+2)) + (r/(x+1)) we first find the value of p. ⇒ 4 = [ ((10x^2 +px+18)/((2x−1)(x+1))) ]_(x = −2) ⇒ 4 = [ ((40−2p+18)/((−1)(−5))) ] = ((58−2p)/5) ⇒20 = 58−2p ; p = 19 now we find the value of q and r. ⇒q = [ ((10x^2 +19x+18)/((x+2)(x+1))) ]_(x = (1/2)) ⇒q = [ (((5/2)+((19)/2)+18)/(((5/2))((3/2)))) ] = ((4×30)/(15)) = 8 ⇒r = [ ((10x^2 +19x+18)/((2x−1)(x+2))) ]_(x = −1) ⇒r = [ ((10−19+18)/((−3)(1))) ] = (9/(−3)) = −3 Thus the value of p−q+2r = 19−8−6= 5](Q118486.png)
Answered by 1549442205PVT last updated on 18/Oct/20
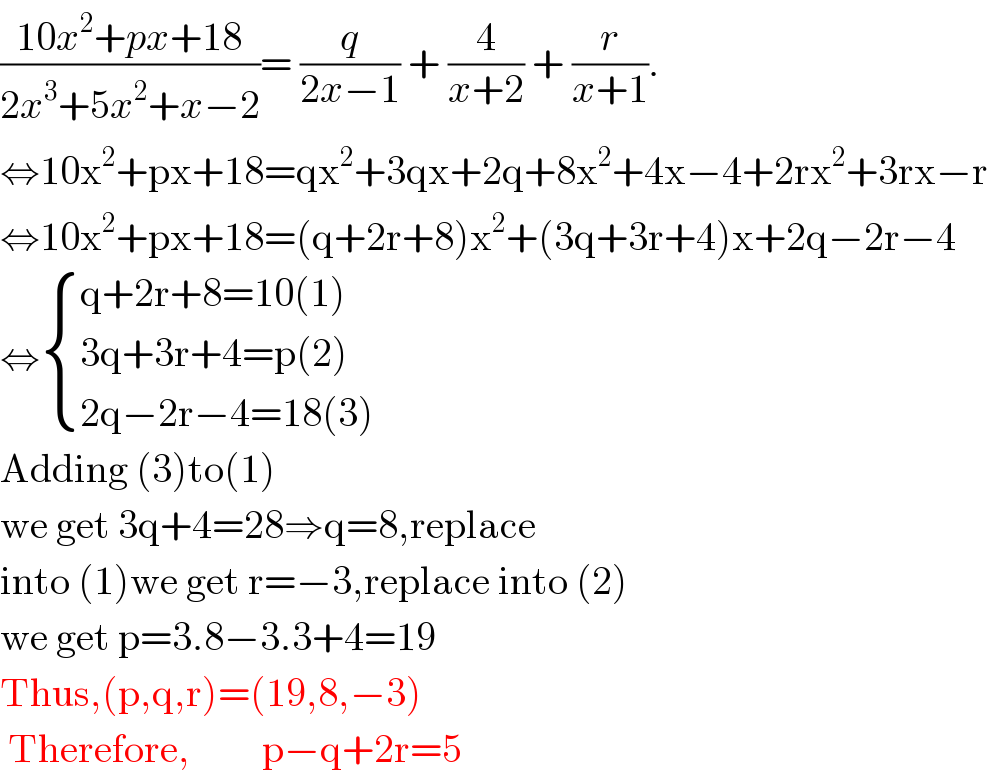
| ||
Question and Answers Forum | ||
Question Number 118485 by bramlexs22 last updated on 18/Oct/20 | ||
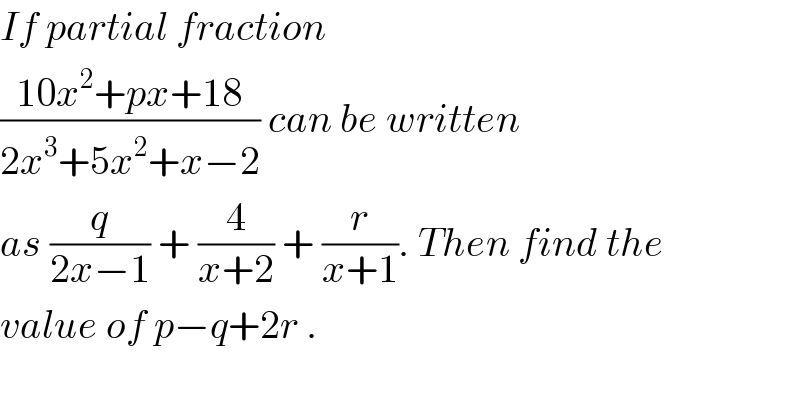 | ||
Answered by benjo_mathlover last updated on 18/Oct/20 | ||
![⇒ ((10x^2 +px+18)/(2x^3 +5x^2 +x−2)) ≡ (q/(2x−1)) + (4/(x+2)) + (r/(x+1)) we first find the value of p. ⇒ 4 = [ ((10x^2 +px+18)/((2x−1)(x+1))) ]_(x = −2) ⇒ 4 = [ ((40−2p+18)/((−1)(−5))) ] = ((58−2p)/5) ⇒20 = 58−2p ; p = 19 now we find the value of q and r. ⇒q = [ ((10x^2 +19x+18)/((x+2)(x+1))) ]_(x = (1/2)) ⇒q = [ (((5/2)+((19)/2)+18)/(((5/2))((3/2)))) ] = ((4×30)/(15)) = 8 ⇒r = [ ((10x^2 +19x+18)/((2x−1)(x+2))) ]_(x = −1) ⇒r = [ ((10−19+18)/((−3)(1))) ] = (9/(−3)) = −3 Thus the value of p−q+2r = 19−8−6= 5](Q118486.png) | ||
| ||
Answered by 1549442205PVT last updated on 18/Oct/20 | ||
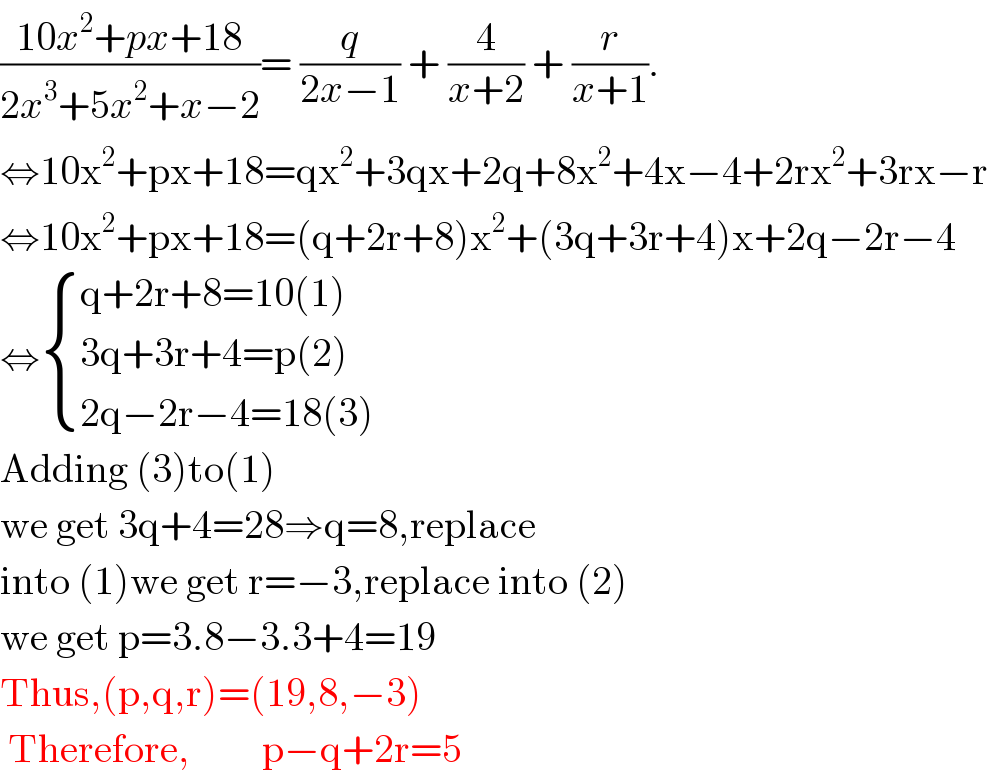 | ||
| ||