
Question Number 118674 by mathace last updated on 19/Oct/20

$${Please}\:{integrate} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{{c}} }{dx}\:{where}\:{c}\:{is}\:{a}\:{constant}. \\ $$
Answered by Dwaipayan Shikari last updated on 19/Oct/20
![∫_0 ^1 Σ_(n=0) ^∞ (−1)^n .x^(nc) dx Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(nc) dx [ (1/(1+x^c ))=Σ_(n=0) ^∞ (−1)^n .x^(nc) ] Σ_(n=0) ^∞ (−1)^n [(x^(nc+1) /(nc+1))]_0 ^1 Σ_(n=0) ^∞ (−1)^n .(1/(nc+1))](Q118675.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .{x}^{{nc}} {dx} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{nc}} {dx}\:\:\:\:\:\:\:\:\:\left[\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{{c}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .{x}^{{nc}} \right] \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \left[\frac{{x}^{{nc}+\mathrm{1}} }{{nc}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .\frac{\mathrm{1}}{{nc}+\mathrm{1}} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Oct/20
![When c=2 Σ_(n=0) ^∞ (−1)^n (1/(2n+1))=1−(1/3)+(1/5)−(1/7)+...=(π/4) ∫_0 ^1 (1/(1+x^2 ))dx=[tan^(−1) x]_0 ^1 =(π/4)](Q118676.png)
$${When} \\ $$$${c}=\mathrm{2} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+...=\frac{\pi}{\mathrm{4}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\left[{tan}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\pi}{\mathrm{4}} \\ $$
Commented by mathace last updated on 19/Oct/20
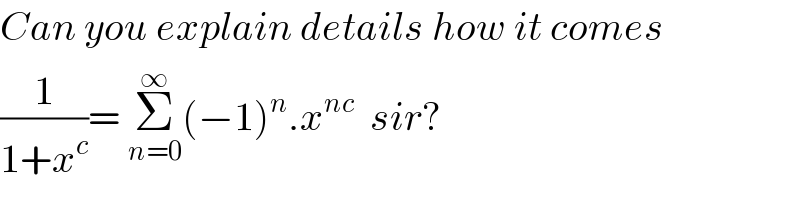
$${Can}\:{you}\:{explain}\:{details}\:{how}\:{it}\:{comes} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{{c}} }=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} .{x}^{{nc}} \:\:{sir}? \\ $$
Commented by Dwaipayan Shikari last updated on 19/Oct/20

$$\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +.....=\frac{\mathrm{1}}{\mathrm{1}−{x}}=\frac{{T}_{\mathrm{1}} }{\mathrm{1}−{R}}\:\:\:\:\:\:\:\:\:\left({T}_{\mathrm{1}} =\:{first}\:{term}\:\:{R}={common}\:{Ratio}\right) \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} =\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +{x}^{\mathrm{4}} −{x}^{\mathrm{5}} +...=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:\:\:\:\:\left({Here}\:{common}\:{Ratio}\:\left(−{x}\right)\right) \\ $$$$\mathrm{1}−{x}^{{c}} +{x}^{\mathrm{2}{c}} −{x}^{\mathrm{3}{c}} +...=\frac{\mathrm{1}}{\mathrm{1}+{x}^{{c}} }\:\:\:\left({Common}\:{Ratio}\:\left(−{x}^{{c}} \right)\right. \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} {x}^{{nc}} =\frac{\mathrm{1}}{\mathrm{1}+{x}^{{c}} } \\ $$
Commented by mathace last updated on 19/Oct/20
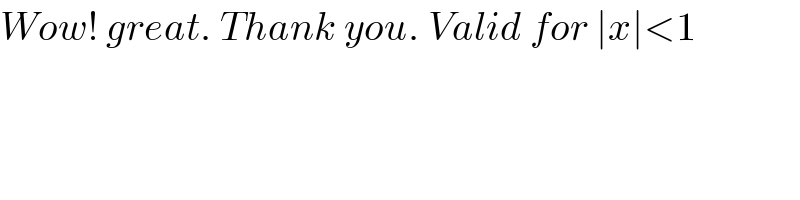
$${Wow}!\:{great}.\:{Thank}\:{you}.\:{Valid}\:{for}\:\mid{x}\mid<\mathrm{1} \\ $$
Commented by Dwaipayan Shikari last updated on 19/Oct/20

$${yes}! \\ $$
Commented by Ar Brandon last updated on 19/Oct/20
��
