
Question and Answers Forum
Question Number 118710 by eric last updated on 19/Oct/20

Answered by mathmax by abdo last updated on 19/Oct/20
![M=∫_0 ^∞ ((lnx)/(1+x^3 ))dx =∫_0 ^1 ((lnx)/(1+x^3 ))dx +∫_1 ^∞ ((lnx)/(1+x^3 ))dx(→x=(1/t)) =∫_0 ^1 ((lnx)/(1+x^3 ))dx −∫_0 ^1 ((−lnt)/(1+(1/t^3 )))×(((−dt)/t^2 )) =∫_0 ^1 ((lnx)/(1+x^3 ))dx−∫_0 ^1 ((tlnt)/(1+t^3 )) dt we have ∫_0 ^1 ((lnx)/(1+x^3 ))dx =∫_0 ^1 lnxΣ_(n=0) ^∞ (−1)^n x^(3n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n) lnx dx U_n =∫_0 ^1 x^(3n) lnxdx =_(byparts) [(x^(3n+1) /(3n+1))lnx]_0 ^1 −∫_0 ^1 (x^(3n) /(3n+1))dx =−(1/((3n+1)^2 )) ⇒∫_0 ^1 ((lnx)/(1+x^3 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) ∫_0 ^1 ((xlnx)/(1+x^3 ))dx =∫_0 ^1 xlnxΣ_(n=0) ^∞ (−1)^n x^(3n) dx=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n+1) lnx dx V_n =∫_0 ^1 x^(3n+1) lnx dx =[(x^(3n+2) /(3n+2))lnx]_0 ^1 −∫_0 ^1 (x^(3n+1) /(3n+2))dx =−(1/((3n+2)^2 )) ⇒∫_0 ^1 ((xlnx)/(1+x^3 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((3n+2)^2 )) ⇒ M =−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) +Σ_(n=0) ^∞ (((−1)^n )/((3n+2)^2 )) rest calculus of those series ...be continued...](Q118724.png)
Commented by mathdave last updated on 19/Oct/20
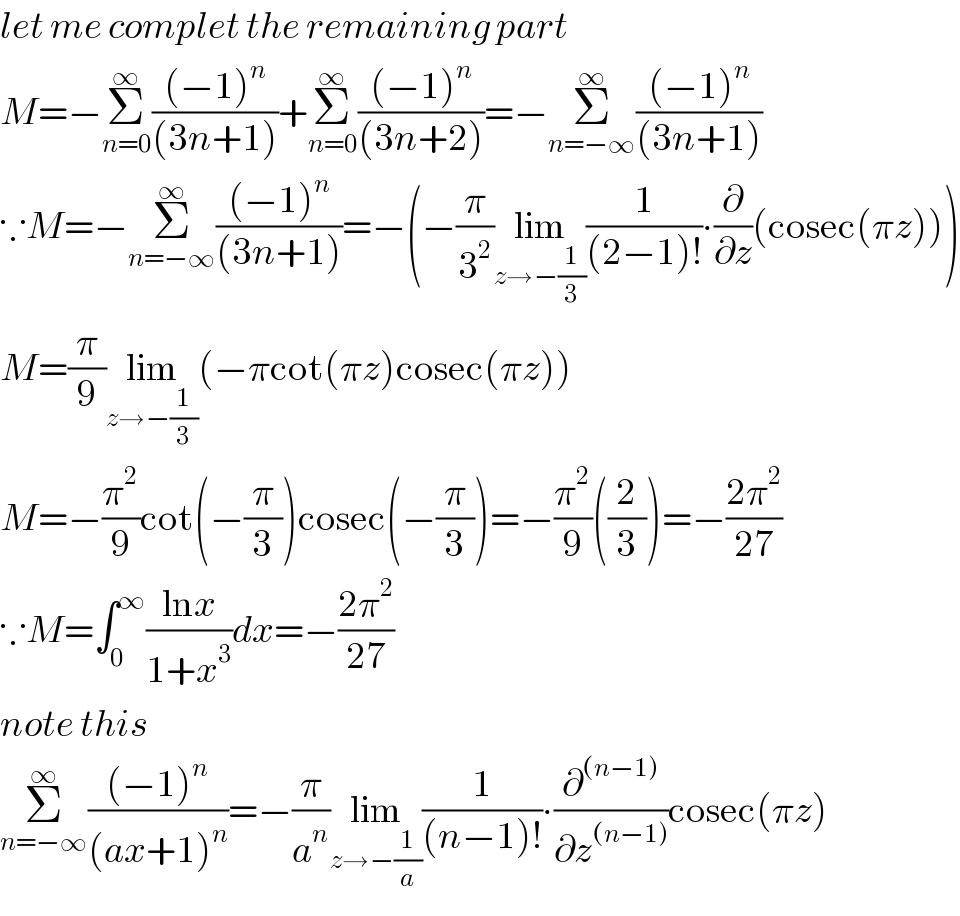
Answered by mnjuly1970 last updated on 19/Oct/20

| ||
Question and Answers Forum | ||
Question Number 118710 by eric last updated on 19/Oct/20 | ||
 | ||
Answered by mathmax by abdo last updated on 19/Oct/20 | ||
![M=∫_0 ^∞ ((lnx)/(1+x^3 ))dx =∫_0 ^1 ((lnx)/(1+x^3 ))dx +∫_1 ^∞ ((lnx)/(1+x^3 ))dx(→x=(1/t)) =∫_0 ^1 ((lnx)/(1+x^3 ))dx −∫_0 ^1 ((−lnt)/(1+(1/t^3 )))×(((−dt)/t^2 )) =∫_0 ^1 ((lnx)/(1+x^3 ))dx−∫_0 ^1 ((tlnt)/(1+t^3 )) dt we have ∫_0 ^1 ((lnx)/(1+x^3 ))dx =∫_0 ^1 lnxΣ_(n=0) ^∞ (−1)^n x^(3n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n) lnx dx U_n =∫_0 ^1 x^(3n) lnxdx =_(byparts) [(x^(3n+1) /(3n+1))lnx]_0 ^1 −∫_0 ^1 (x^(3n) /(3n+1))dx =−(1/((3n+1)^2 )) ⇒∫_0 ^1 ((lnx)/(1+x^3 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) ∫_0 ^1 ((xlnx)/(1+x^3 ))dx =∫_0 ^1 xlnxΣ_(n=0) ^∞ (−1)^n x^(3n) dx=Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(3n+1) lnx dx V_n =∫_0 ^1 x^(3n+1) lnx dx =[(x^(3n+2) /(3n+2))lnx]_0 ^1 −∫_0 ^1 (x^(3n+1) /(3n+2))dx =−(1/((3n+2)^2 )) ⇒∫_0 ^1 ((xlnx)/(1+x^3 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/((3n+2)^2 )) ⇒ M =−Σ_(n=0) ^∞ (((−1)^n )/((3n+1)^2 )) +Σ_(n=0) ^∞ (((−1)^n )/((3n+2)^2 )) rest calculus of those series ...be continued...](Q118724.png) | ||
| ||
Commented by mathdave last updated on 19/Oct/20 | ||
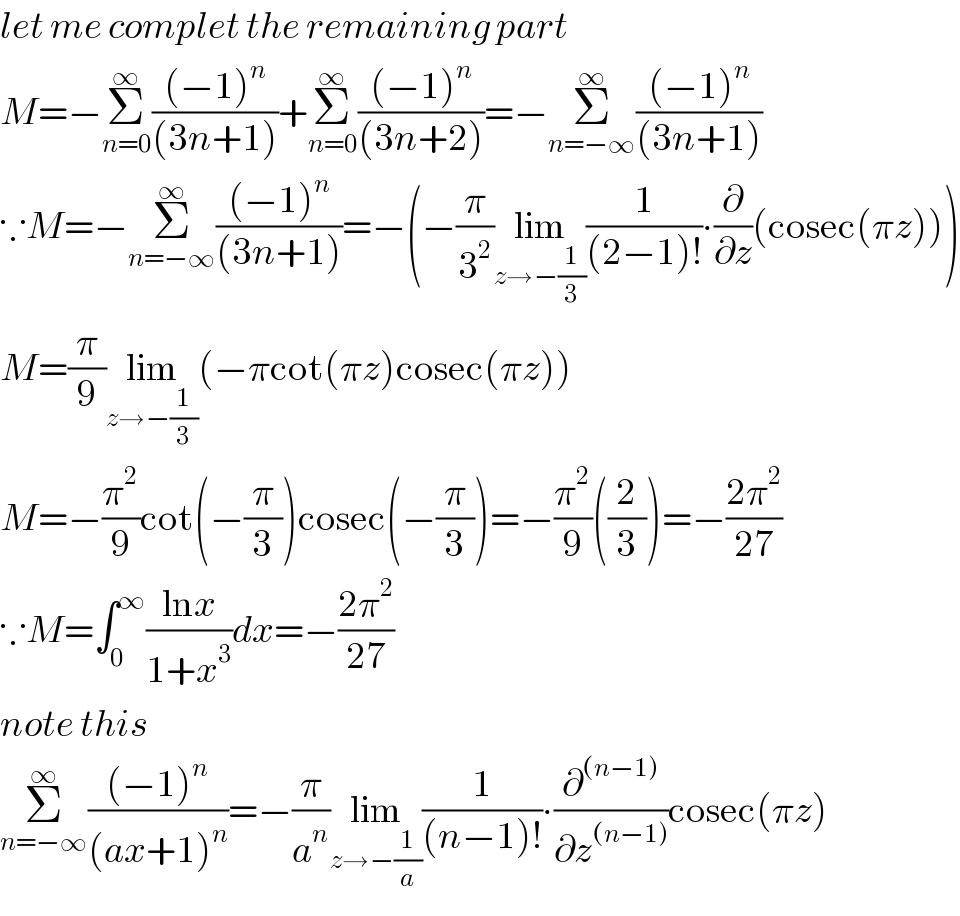 | ||
Answered by mnjuly1970 last updated on 19/Oct/20 | ||
 | ||
| ||