Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 118733 by mohammad17 last updated on 19/Oct/20

Commented by bemath last updated on 19/Oct/20

(4) (d/dx) [ ∫ _x^3 ^(2x^2 ) cos (2t^3 +1) dt ] = 4x cos (2.(8x^6 )+1)−3x^2 cos (2.x^9 +1) =4x cos (16x^6 +1)−3x^2 cos (2x^9 +1)

$$\left(\mathrm{4}\right)\:\frac{{d}}{{dx}}\:\left[\:\int\:_{{x}^{\mathrm{3}} } ^{\mathrm{2}{x}^{\mathrm{2}} } \:\mathrm{cos}\:\left(\mathrm{2}{t}^{\mathrm{3}} +\mathrm{1}\right)\:{dt}\:\right]\:= \\ $$$$\mathrm{4}{x}\:\mathrm{cos}\:\left(\mathrm{2}.\left(\mathrm{8}{x}^{\mathrm{6}} \right)+\mathrm{1}\right)−\mathrm{3}{x}^{\mathrm{2}} \mathrm{cos}\:\left(\mathrm{2}.{x}^{\mathrm{9}} +\mathrm{1}\right) \\ $$$$=\mathrm{4}{x}\:\mathrm{cos}\:\left(\mathrm{16}{x}^{\mathrm{6}} +\mathrm{1}\right)−\mathrm{3}{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\mathrm{2}{x}^{\mathrm{9}} +\mathrm{1}\right) \\ $$

Answered by TANMAY PANACEA last updated on 19/Oct/20

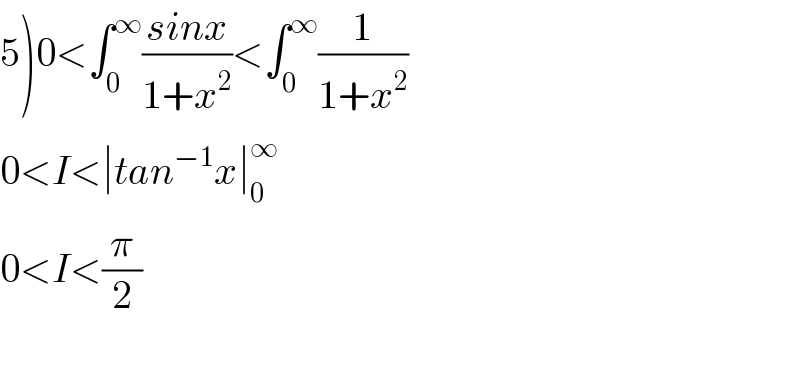
5)0<∫_0 ^∞ ((sinx)/(1+x^2 ))<∫_0 ^∞ (1/(1+x^2 )) 0<I<∣tan^(−1) x∣_0 ^∞ 0<I<(π/2)

$$\left.\mathrm{5}\right)\mathrm{0}<\int_{\mathrm{0}} ^{\infty} \frac{{sinx}}{\mathrm{1}+{x}^{\mathrm{2}} }<\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\mathrm{0}<{I}<\mid{tan}^{−\mathrm{1}} {x}\mid_{\mathrm{0}} ^{\infty} \\ $$$$\mathrm{0}<{I}<\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$

Answered by TANMAY PANACEA last updated on 19/Oct/20

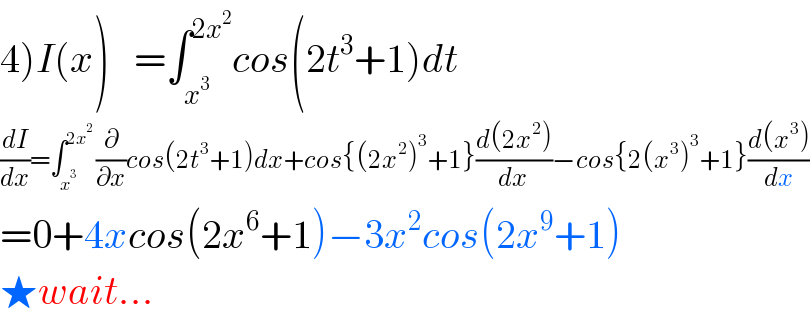
4)I(x) =∫_x^3 ^(2x^2 ) cos(2t^3 +1)dt (dI/dx)=∫_x^3 ^(2x^2 ) (∂/∂x)cos(2t^3 +1)dx+cos{(2x^2 )^3 +1}((d(2x^2 ))/dx)−cos{2(x^3 )^3 +1}((d(x^3 ))/dx) =0+4xcos(2x^6 +1)−3x^2 cos(2x^9 +1) ★wait...

$$\left.\mathrm{4}\right){I}\left({x}\right)\:\:\:=\int_{{x}^{\mathrm{3}} } ^{\mathrm{2}{x}^{\mathrm{2}} } {cos}\left(\mathrm{2}{t}^{\mathrm{3}} +\mathrm{1}\right){dt} \\ $$$$\frac{{dI}}{{dx}}=\int_{{x}^{\mathrm{3}} } ^{\mathrm{2}{x}^{\mathrm{2}} } \:\frac{\partial}{\partial{x}}{cos}\left(\mathrm{2}{t}^{\mathrm{3}} +\mathrm{1}\right){dx}+{cos}\left\{\left(\mathrm{2}{x}^{\mathrm{2}} \right)^{\mathrm{3}} +\mathrm{1}\right\}\frac{{d}\left(\mathrm{2}{x}^{\mathrm{2}} \right)}{{dx}}−{cos}\left\{\mathrm{2}\left({x}^{\mathrm{3}} \right)^{\mathrm{3}} +\mathrm{1}\right\}\frac{{d}\left({x}^{\mathrm{3}} \right)}{{dx}} \\ $$$$=\mathrm{0}+\mathrm{4}{xcos}\left(\mathrm{2}{x}^{\mathrm{6}} +\mathrm{1}\right)−\mathrm{3}{x}^{\mathrm{2}} {cos}\left(\mathrm{2}{x}^{\mathrm{9}} +\mathrm{1}\right) \\ $$$$\bigstar{wait}... \\ $$

Answered by TANMAY PANACEA last updated on 19/Oct/20

i)I=∫_0 ^(π/2) ((sin^3 x)/(cos^3 x+sin^3 x))dx I=∫_0 ^(π/2) ((cos^3 x)/(sin^3 x+cos^3 x))dx [using ∫_0 ^a f(x)dx =∫_0 ^a f(a−x)dx] 2I=∫_0 ^(π/2) dx→I=(π/4)

$$\left.{i}\right){I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sin}^{\mathrm{3}} {x}}{{cos}^{\mathrm{3}} {x}+{sin}^{\mathrm{3}} {x}}{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cos}^{\mathrm{3}} {x}}{{sin}^{\mathrm{3}} {x}+{cos}^{\mathrm{3}} {x}}{dx}\:\:\left[{using}\:\int_{\mathrm{0}} ^{{a}} {f}\left({x}\right){dx}\:=\int_{\mathrm{0}} ^{{a}} {f}\left({a}−{x}\right){dx}\right] \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx}\rightarrow{I}=\frac{\pi}{\mathrm{4}} \\ $$

Answered by TANMAY PANACEA last updated on 19/Oct/20

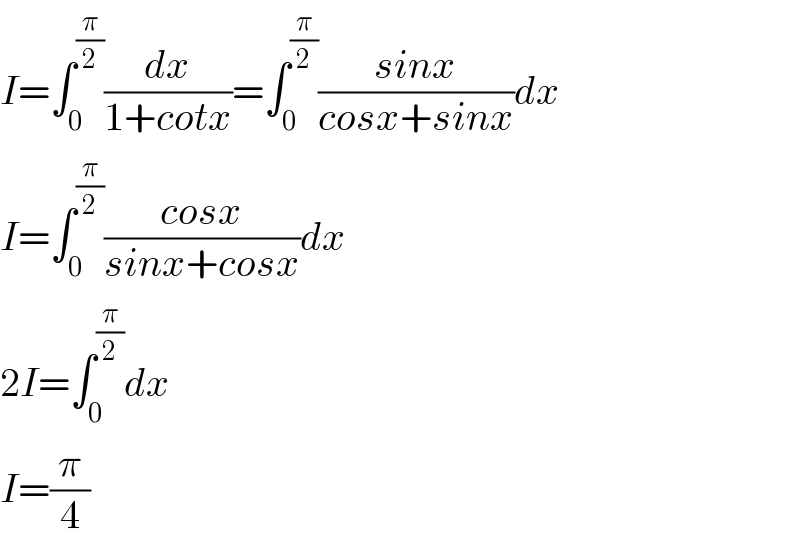
I=∫_0 ^(π/2) (dx/(1+cotx))=∫_0 ^(π/2) ((sinx)/(cosx+sinx))dx I=∫_0 ^(π/2) ((cosx)/(sinx+cosx))dx 2I=∫_0 ^(π/2) dx I=(π/4)

$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}+{cotx}}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{sinx}}{{cosx}+{sinx}}{dx} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{sinx}+{cosx}}{dx} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {dx} \\ $$$${I}=\frac{\pi}{\mathrm{4}} \\ $$

Commented by mnjuly1970 last updated on 19/Oct/20

thank you mr tanmay.. .m.n.july.1970..

$${thank}\:{you}\:{mr}\:{tanmay}.. \\ $$$$.{m}.{n}.{july}.\mathrm{1970}.. \\ $$

Commented by TANMAY PANACEA last updated on 19/Oct/20

most welcome sir

$${most}\:{welcome}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com