
Question and Answers Forum
Question Number 118819 by bramlexs22 last updated on 20/Oct/20
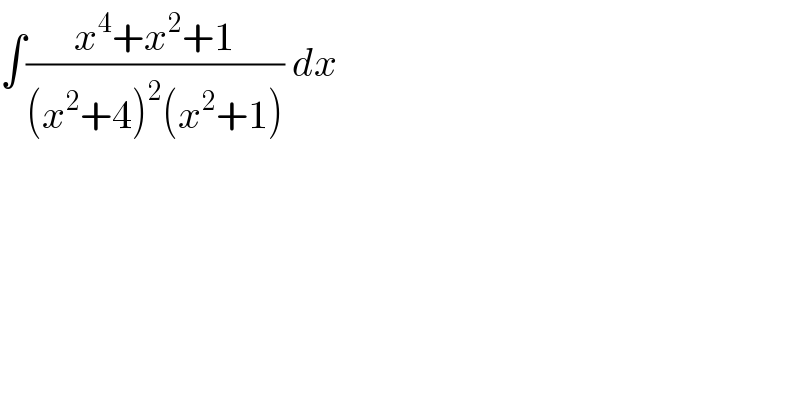
Answered by MJS_new last updated on 20/Oct/20
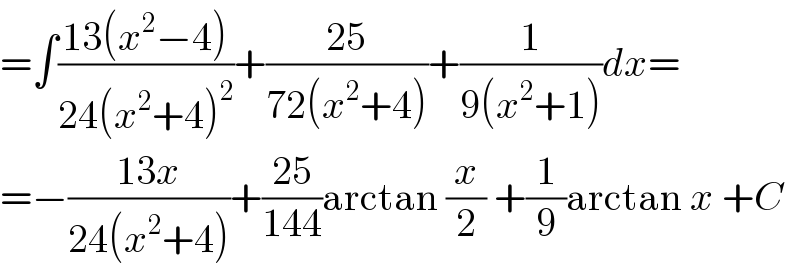
Answered by bobhans last updated on 20/Oct/20

Answered by 1549442205PVT last updated on 21/Oct/20
![((x^4 +x^2 +1)/((x^2 +4)^2 (x^2 +1))) =((ax^3 +bx^2 +cx+d)/(x^4 +8x^2 +16))+((ex+f)/(x^2 +1)) ⇔x^4 +x^2 +1=(a+e)x^5 +(b+f)x^4 +(a+c+8e)x^3 +(b+d+8f)x^2 +(c+16e)x+d+16f ⇔ { ((a+e=0)),((b+f=1)),((a+c+8e=0)),((b+d+8f=1)),((c+16e=0)),((d+16f=1)) :}⇔ { ((a=c=e=0)),((b=8/9)),((d=−7/9)),((f=1/9)) :} F=∫(((x^4 +x^2 +1)dx)/((x^2 +4)^2 (x^2 +1))) =∫(((8x^2 −7)/(9(x^2 +4)^2 ))+(1/(9(x^2 +1))))dx =(8/9)∫((((x^2 +4)−11)/((x^2 +4)^2 ))+(1/(9(x^2 +1))))dx =(8/9)∫(dx/(x^2 +4))−∫((88dx)/(9(x^2 +4)^2 ))+∫(dx/(9(x^2 +1))) =(4/9)tan^(−1) ((x/2))+(1/9)tan^(−1) (x)−((88)/9)A A=(1/(2.4)).(x/(x^2 +4))+(1/4).(1/2)∫(dx/(x^2 +4)) =(x/(8(x^2 +4)))+(1/8)×(1/2)tan^(−1) (x/2) F=(4/9)tan^(−1) ((x/2))+(1/9)tan^(−1) (x)−((88)/9)[ (1/8)((x/(x^2 +4))+(1/2)tan^(−1) ((x/2)))] =((−1)/6)tan^(−1) ((x/2))+(1/9)tan^(−1) (x) −((11)/9).(x/(x^2 +4))+C](Q118852.png)
| ||
Question and Answers Forum | ||
Question Number 118819 by bramlexs22 last updated on 20/Oct/20 | ||
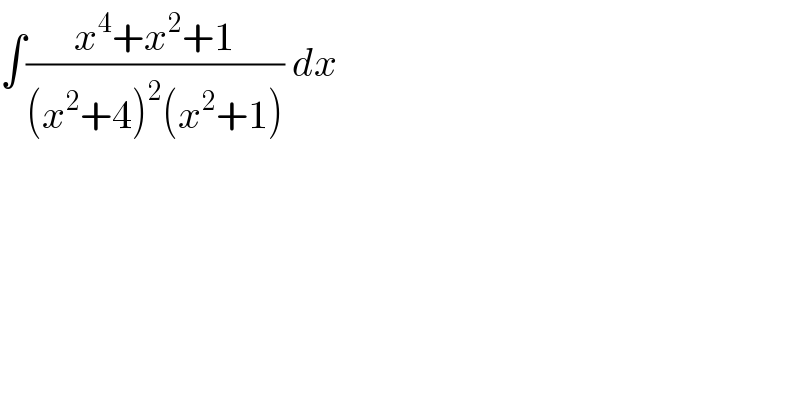 | ||
Answered by MJS_new last updated on 20/Oct/20 | ||
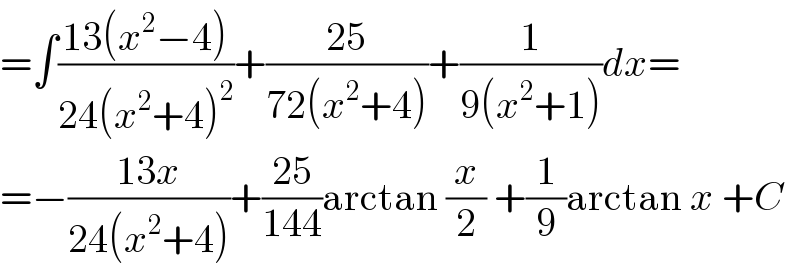 | ||
| ||
Answered by bobhans last updated on 20/Oct/20 | ||
 | ||
| ||
Answered by 1549442205PVT last updated on 21/Oct/20 | ||
![((x^4 +x^2 +1)/((x^2 +4)^2 (x^2 +1))) =((ax^3 +bx^2 +cx+d)/(x^4 +8x^2 +16))+((ex+f)/(x^2 +1)) ⇔x^4 +x^2 +1=(a+e)x^5 +(b+f)x^4 +(a+c+8e)x^3 +(b+d+8f)x^2 +(c+16e)x+d+16f ⇔ { ((a+e=0)),((b+f=1)),((a+c+8e=0)),((b+d+8f=1)),((c+16e=0)),((d+16f=1)) :}⇔ { ((a=c=e=0)),((b=8/9)),((d=−7/9)),((f=1/9)) :} F=∫(((x^4 +x^2 +1)dx)/((x^2 +4)^2 (x^2 +1))) =∫(((8x^2 −7)/(9(x^2 +4)^2 ))+(1/(9(x^2 +1))))dx =(8/9)∫((((x^2 +4)−11)/((x^2 +4)^2 ))+(1/(9(x^2 +1))))dx =(8/9)∫(dx/(x^2 +4))−∫((88dx)/(9(x^2 +4)^2 ))+∫(dx/(9(x^2 +1))) =(4/9)tan^(−1) ((x/2))+(1/9)tan^(−1) (x)−((88)/9)A A=(1/(2.4)).(x/(x^2 +4))+(1/4).(1/2)∫(dx/(x^2 +4)) =(x/(8(x^2 +4)))+(1/8)×(1/2)tan^(−1) (x/2) F=(4/9)tan^(−1) ((x/2))+(1/9)tan^(−1) (x)−((88)/9)[ (1/8)((x/(x^2 +4))+(1/2)tan^(−1) ((x/2)))] =((−1)/6)tan^(−1) ((x/2))+(1/9)tan^(−1) (x) −((11)/9).(x/(x^2 +4))+C](Q118852.png) | ||
| ||