sin ((π/(14)))sin (((2π)/(14)))sin (((3π)/(14)))...sin (((6π)/(14)))=?


Question and Answers Forum

All Questions Topic List
Trigonometry Questions
Previous in All Question Next in All Question
Previous in Trigonometry Next in Trigonometry
Question Number 118899 by bobhans last updated on 20/Oct/20

$\sin (\frac{π}{14}) \sin (\frac{2 π}{14}) \sin (\frac{3 π}{14}) . . . \sin (\frac{6 π}{14}) = ?$
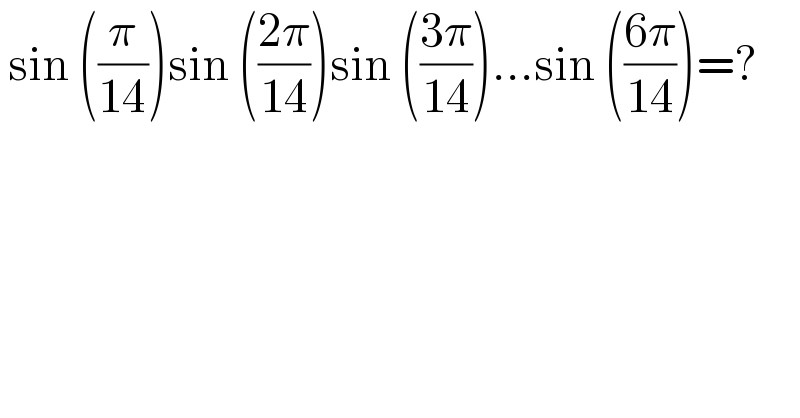
	Answered by TANMAY PANACEA last updated on 20/Oct/20

	$t a k i n g h e l p f r o m S . L L o n e y T r i g o n o m e t r y$ $2^{\frac{n - 1}{2}} s i n (\frac{2 π}{2 n}) s i n (\frac{4 π}{2 n}) s i n (\frac{6 π}{2 n}) . . . s i n (\frac{n - 2}{2 n}) π = \sqrt{n}$ $p = s i n (\frac{2 π}{28}) s i n (\frac{4 π}{28}) s i n (\frac{6 π}{28}) s i n (\frac{8 π}{28}) s i n (\frac{10 π}{28}) s i n (\frac{12 π}{28})$ $s o c o m p a r i n g$ $2 n = 28 \to n = 14$ $r e q u i r e d a n s w e r = \frac{\sqrt{n}}{2^{\frac{n - 1}{2}}}$ $= \frac{\sqrt{14}}{2^{\frac{13}{2}}} = \frac{\sqrt{7} \times \sqrt{2}}{2^{6} \times \sqrt{2}} = \frac{\sqrt{7}}{2^{6}} A n s w e r$
	Commented by TANMAY PANACEA last updated on 20/Oct/20

	Answered by mindispower last updated on 20/Oct/20

	$l e t z^{14} - 1 = 0$ $\Rightarrow z^{14} - 1 = \underset{k = 0}{\prod^{13}} (X - e^{\frac{2 i k π}{14}}) \Rightarrow \underset{k = 1}{\prod^{13}} (1 - e^{\frac{2 i k π}{14}}) = 14$ $(1 - e^{\frac{2 i k π}{14}}) = e^{\frac{i k π}{14}} (e^{\frac{- i k π}{14}} - e^{\frac{i k π}{14}})$ $= - 2 i s i n (\frac{k π}{14}) e^{i k \frac{π}{14}}$ $\Rightarrow \underset{k = 1}{\prod^{13}} (- 2 i s i n (\frac{k π}{14})) . e^{i \frac{π}{14} Σ k}) = 14$ $\Rightarrow {(- 2 i)}^{13} \underset{k = 1}{\prod^{6}} s i n (\frac{k π}{14}) . \underset{k = 7}{\prod^{13}} s i n (\frac{k π}{14}) e^{i \frac{π}{14} (7.13)} = 14$ $\Rightarrow {(- 2)}^{13} . i . \underset{k = 1}{\prod^{6}} s i n (\frac{k π}{14}) . \underset{k = 1}{\prod^{7}} s i n (\frac{(14 - k) π}{14}) e^{\frac{1}{2} 13 i π} = 14$ $s i n (π - x) = s i n (x), s i n (\frac{7 π}{14}) = s i n (\frac{π}{2}) = 1, e^{\frac{13 i π}{2}} = i$ $\Rightarrow {(2)}^{13} {[\underset{k = 1}{\prod^{6}} s i n (\frac{k π}{14})]}^{2} = 14$ $\Rightarrow \underset{k = 1}{\prod^{6}} s i n (\frac{k π}{14}) = \frac{\sqrt{7}}{2^{6}}$
	Commented by TANMAY PANACEA last updated on 20/Oct/20

	$e x c e l l e n t s i f$
	Commented by TANMAY PANACEA last updated on 20/Oct/20

	$s i r$
	Commented by mindispower last updated on 20/Oct/20

	$t h a n k y o u s i r$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum