
Question and Answers Forum
Previous in Differential Equation Next in Differential Equation
Question Number 118975 by benjo_mathlover last updated on 21/Oct/20
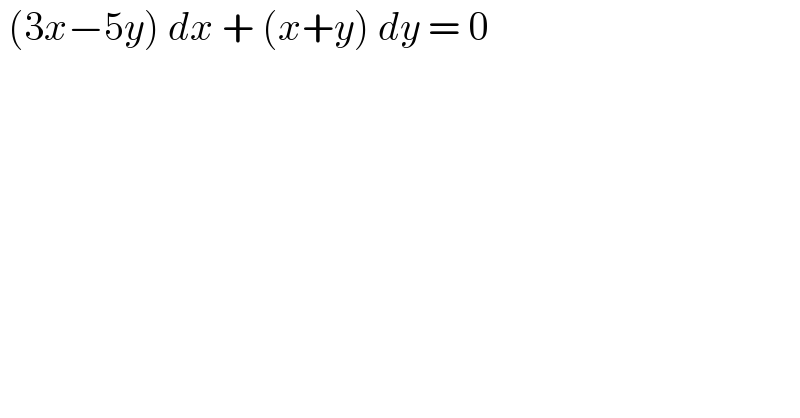
Answered by 1549442205PVT last updated on 21/Oct/20
![(3x−5y) dx + (x+y) dy = 0(1) Put y=xt⇒dy=xdt+tdx (1)⇔(3x−5xt)dx+(x+xt)(xdt+tdx) ⇔[3−5t+t(1+t)]dx+(1+t)xdt=0 ⇔(t^2 −4t+3)dx+(1+t)xdt=0 ⇔−(dx/x)=(((1+t)dt)/(t^2 −4t+3))⇔((−dx)/x)=(((1+t)dt)/((t−1)(t−3))) Integrating two sides we get −ln∣x∣+lnC=∫(2/(t−3))dt−∫(1/(t−1))dt =ln∣(((t−3)^2 )/(t−1))∣⇔ln(C/(∣x∣))=ln∣(((t−3)^2 )/(t−1))∣ ⇔(C/(∣x∣))=(((t−3)^2 )/(t−1))⇔(C/(∣x∣))=((((y/x)−3)^2 )/(∣((y/x)−1)∣)) ⇔C=(((y−3x)^2 )/(x^2 ∣y−x∣))(C>0−constant)](Q118976.png)
Answered by benjo_mathlover last updated on 21/Oct/20

