Question Number 119038 by MJS_new last updated on 21/Oct/20
$$\underset{−\pi/\mathrm{4}} {\overset{+\pi/\mathrm{4}} {\int}}\frac{\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}}{\:\sqrt{\mathrm{1}−\mathrm{tan}\:{x}}}{dx} \\ $$
Answered by mindispower last updated on 21/Oct/20
![=∫_(−(π/4)) ^(π/4) ((√(1−tg(x)))/( (√(1+tg(x)))))dx,I=∫((√(1+tg(x)))/( (√(1−tg(x)))))dx 2I=∫_(−(π/4) ) ^(π/4) (((√(1−tg(x)))/( (√(1+tg(x)))))+((√(1+tg(x)))/( (√(1−tg(x))))))dx =∫_(−(π/4)) ^(π/4) ((1−tg(x)+1+tg(x))/( (√(1−tg^2 (x)))))dx=2∫(dx/( (√(1−tg^2 (x))))) I=∫_(−(π/4)) ^(π/4) (dx/( (√(1−tg^2 (x)))))=2∫_0 ^(π/4) (dx/( (√(1−tg^2 (x))))) let tg(x)=t⇒x=arctan(t)⇒dx=(dt/(1+t^2 )) ⇒2∫_0 ^1 (dt/( (√(1−t^2 ))(1+t^2 ))) t=sin(w)⇒dt=cos(w),(√(1−t^2 ))=cos(w) ⇔2∫_0 ^(π/2) (dw/(1+sin^2 (w)))=2∫(dw/(1+cos^2 (w))) =2∫_0 ^(π/2) (1/(cos^2 (w)(2+tg^2 (w))))=2∫_0 ^(π/2) ((d(tg(w)))/(2+tg^2 (w))) =∫_0 ^(π/2) ((d(tg(w)))/(1+(((tg(w))/( (√2))))^2 ))=(√2)[arctan(((tg(w))/( (√2))))]_0 ^(π/2) (π/2).(√2)=(π/( (√2))),may bee son mistacks](Q119040.png)
$$=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \frac{\sqrt{\mathrm{1}−{tg}\left({x}\right)}}{\:\sqrt{\mathrm{1}+{tg}\left({x}\right)}}{dx},{I}=\int\frac{\sqrt{\mathrm{1}+{tg}\left({x}\right)}}{\:\sqrt{\mathrm{1}−{tg}\left({x}\right)}}{dx} \\ $$$$\mathrm{2}{I}=\int_{−\frac{\pi}{\mathrm{4}}\:} ^{\frac{\pi}{\mathrm{4}}} \left(\frac{\sqrt{\mathrm{1}−{tg}\left({x}\right)}}{\:\sqrt{\mathrm{1}+{tg}\left({x}\right)}}+\frac{\sqrt{\mathrm{1}+{tg}\left({x}\right)}}{\:\sqrt{\mathrm{1}−{tg}\left({x}\right)}}\right){dx} \\ $$$$=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}−{tg}\left({x}\right)+\mathrm{1}+{tg}\left({x}\right)}{\:\sqrt{\mathrm{1}−{tg}^{\mathrm{2}} \left({x}\right)}}{dx}=\mathrm{2}\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{tg}^{\mathrm{2}} \left({x}\right)}} \\ $$$${I}=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \frac{{dx}}{\:\sqrt{\mathrm{1}−{tg}^{\mathrm{2}} \left({x}\right)}}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{dx}}{\:\sqrt{\mathrm{1}−{tg}^{\mathrm{2}} \left({x}\right)}} \\ $$$${let}\:{tg}\left({x}\right)={t}\Rightarrow{x}={arctan}\left({t}\right)\Rightarrow{dx}=\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\left(\mathrm{1}+{t}^{\mathrm{2}} \right)} \\ $$$${t}={sin}\left({w}\right)\Rightarrow{dt}={cos}\left({w}\right),\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }={cos}\left({w}\right) \\ $$$$\Leftrightarrow\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dw}}{\mathrm{1}+{sin}^{\mathrm{2}} \left({w}\right)}=\mathrm{2}\int\frac{{dw}}{\mathrm{1}+{cos}^{\mathrm{2}} \left({w}\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({w}\right)\left(\mathrm{2}+{tg}^{\mathrm{2}} \left({w}\right)\right)}=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tg}\left({w}\right)\right)}{\mathrm{2}+{tg}^{\mathrm{2}} \left({w}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left({tg}\left({w}\right)\right)}{\mathrm{1}+\left(\frac{{tg}\left({w}\right)}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{2}}\left[{arctan}\left(\frac{{tg}\left({w}\right)}{\:\sqrt{\mathrm{2}}}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$\frac{\pi}{\mathrm{2}}.\sqrt{\mathrm{2}}=\frac{\pi}{\:\sqrt{\mathrm{2}}},{may}\:{bee}\:{son}\:{mistacks}\: \\ $$
Commented by MJS_new last updated on 21/Oct/20
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{I}\:\mathrm{get}\:\mathrm{the}\:\mathrm{same}\:\mathrm{answer} \\ $$
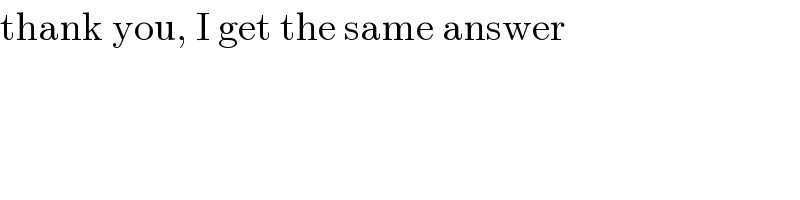
Commented by mindispower last updated on 21/Oct/20
$${withe}\:{pleasur}\:{sir} \\ $$
Commented by $@y@m last updated on 22/Oct/20
@mindispower. Please expain me first line of the solution. How signs of Numerator and Denominator got interchanged?
Commented by Dwaipayan Shikari last updated on 22/Oct/20
$$\int_{\frac{−\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{1}−{tanx}}{\mathrm{1}+{tanx}}}\:=\int_{−\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{\mathrm{1}+{tanx}}{\mathrm{1}−{tanx}}} \\ $$$${Because} \\ $$$$\int_{{q}} ^{{p}} {f}\left({x}\right){dx}=\int_{{q}} ^{{p}} {f}\left({p}+{q}−{x}\right){dx} \\ $$
Commented by $@y@m last updated on 22/Oct/20
@Dwaipayan অনেক ধন্যবাদ. আমি ভুলে গেছিলাম.
Commented by Dwaipayan Shikari last updated on 22/Oct/20
ধন্যবাদ। আপনি কোথায় থাকেন?
Commented by $@y@m last updated on 22/Oct/20
রাঁচি
Commented by MJS_new last updated on 22/Oct/20
Beautiful letters! Sadly I cannot read them.
Commented by Dwaipayan Shikari last updated on 22/Oct/20
first comment Many thanks I have forgotten second comment Thanking you. Where do you live? third comment Ranchi fourth comment সুন্দর হরফ! দু:খিত আমি এটা পড়তে পাচ্ছি না
Answered by $@y@m last updated on 22/Oct/20
![∫((√(1+tan x))/( (√(1−tan x))))dx =∫(√((cos x+sin x)/(cos x−sin x)))dx =∫(√(((cos x+sin x)/(cos x−sin x))×((cos x+sin x)/(cos x+sin x))))dx =∫(√(((cos x+sin x)^2 )/(cos^2 x−sin^2 x)))dx =∫((cos x+sin x)/( (√()cos^2 x−sin^2 x)))dx =∫((cos x)/( (√(1−2sin^2 x))))dx+∫((sin x)/( (√(2cos^2 x−1))))dx =∫_(−(1/( (√2)))) ^(1/( (√2))) (dp/( (√(1−2p^2 ))))−∫_(1/( (√2))) ^(1/( (√2))) (dq/( (√(2q^2 −1)))) =(1/( (√2)))[sin^(−1) ((√2)p)]_(−(1/( (√2)))) ^(1/( (√2))) +0 =(1/( (√2))){sin^(−1) (1)−sin^(−1) (−1)} =(1/( (√2)))((π/2)−((−π)/2)) =(π/( (√2)))](Q119077.png)
$$\int\frac{\sqrt{\mathrm{1}+\mathrm{tan}\:{x}}}{\:\sqrt{\mathrm{1}−\mathrm{tan}\:{x}}}{dx} \\ $$$$=\int\sqrt{\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}}{dx} \\ $$$$=\int\sqrt{\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}−\mathrm{sin}\:{x}}×\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}}{dx} \\ $$$$=\int\sqrt{\frac{\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)^{\mathrm{2}} }{\mathrm{cos}^{\mathrm{2}} \:{x}−\mathrm{sin}^{\mathrm{2}} \:{x}}}{dx} \\ $$$$=\int\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\left.\:\sqrt{\left(\right.}\mathrm{cos}^{\mathrm{2}} \:{x}−\mathrm{sin}^{\mathrm{2}} \:{x}\right)}{dx} \\ $$$$=\int\frac{\mathrm{cos}\:{x}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}}}{dx}+\int\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{2cos}\:^{\mathrm{2}} {x}−\mathrm{1}}}{dx} \\ $$$$=\underset{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\overset{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\int}}\frac{{dp}}{\:\sqrt{\mathrm{1}−\mathrm{2}{p}^{\mathrm{2}} }}−\underset{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\overset{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\int}}\frac{{dq}}{\:\sqrt{\mathrm{2}{q}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left[\mathrm{sin}^{−\mathrm{1}} \left(\sqrt{\mathrm{2}}{p}\right)\underset{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\overset{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} {\right]}}+\mathrm{0} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left\{\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}\right)−\mathrm{sin}^{−\mathrm{1}} \left(−\mathrm{1}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\pi}{\mathrm{2}}−\frac{−\pi}{\mathrm{2}}\right) \\ $$$$=\frac{\pi}{\:\sqrt{\mathrm{2}}} \\ $$
Commented by MJS_new last updated on 22/Oct/20
$$\mathrm{thank}\:\mathrm{you} \\ $$