
Question and Answers Forum
Question Number 119052 by shahria14 last updated on 21/Oct/20
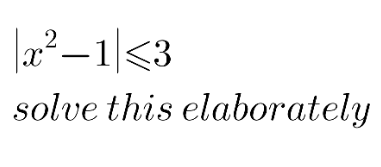
Answered by 1549442205PVT last updated on 22/Oct/20
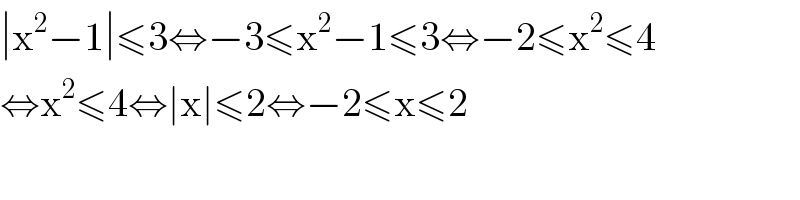
Commented by MJS_new last updated on 22/Oct/20
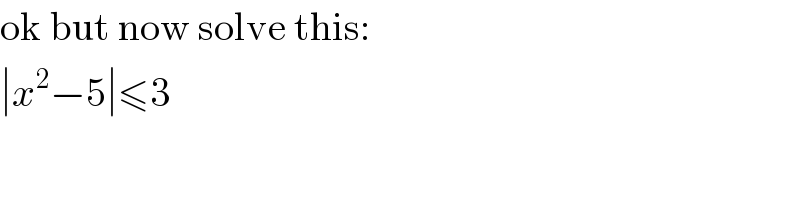
Commented by bemath last updated on 23/Oct/20
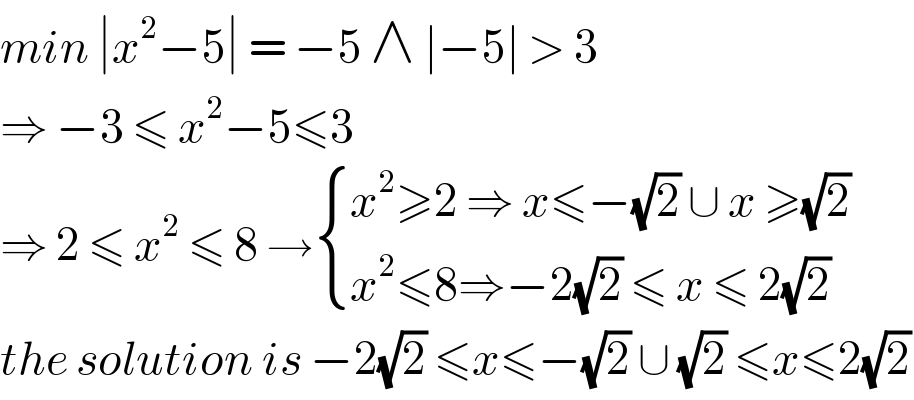
Answered by MJS_new last updated on 22/Oct/20
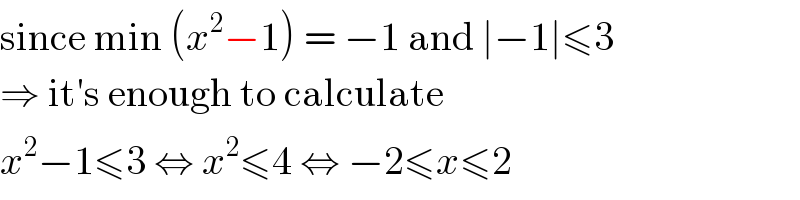
Commented by bemath last updated on 22/Oct/20
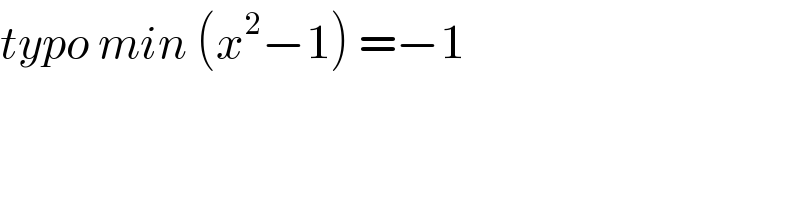
Commented by MJS_new last updated on 22/Oct/20
Answered by Bird last updated on 21/Oct/20
![∣x^2 −1∣≤3 ⇒∣x^2 −1∣−3≤0 ⇒f(x)≤0 sith f(x)=∣x^2 −1∣−3 x −∞ −1 1 +∞ ∣x^2 −1∣ x^2 −1 0 1−x^2 0 x^2 −1 f(x) x^2 −4 −2−x^2 x^2 −4 if x≤−1 f(x)≤0 ⇒x^2 −4 ≤0 ⇒ −2≤x≤2 ⇒S_1 =[−2,−1] if x∈[−1,1] f(x)≤0 ⇒−2−x^2 ≤0 ⇒ 2+x^2 ≥0 ⇒S_2 =[−1,1] if x≥1 f(x)≤0 ⇒x^2 −4≤0 ⇒ −2≤x≤2 ⇒S_3 =[1,2] ⇒ S=∪S_i =[−2,2]](Q119063.png)
