solve (D^2 −2D+1)y = e^x ln x by using the method of variation of parameters.


Question and Answers Forum

All Questions Topic List
Differential Equation Questions
Previous in All Question Next in All Question
Previous in Differential Equation Next in Differential Equation
Question Number 119065 by benjo_mathlover last updated on 21/Oct/20

$s o l v e (D^{2} - 2 D + 1) y = e^{x} \ln x$ $b y u s i n g t h e m e t h o d o f v a r i a t i o n$ $o f p a r a m e t e r s .$
	Answered by Olaf last updated on 22/Oct/20

	$y = e^{x} u$ $y^{'} = (u^{'} + u) e^{x}$ $y^{″} = (u^{″} + 2 u^{'} + u) e^{x}$ $u^{″} + 2 u^{'} + u - 2 (u^{'} + u) + u = \ln x$ $u^{″} = \ln x$ $u^{'} = \int \ln x d x = x \ln x - x + C_{1}$ $u = \int (x \ln x - x + C_{1}) d x$ $u = \frac{x^{2}}{2} \ln x - \int \frac{x^{2}}{2} . \frac{1}{x} d x - \frac{x^{2}}{2} + C_{1} x + C_{2}$ $u = \frac{x^{2}}{2} \ln x - \frac{x^{2}}{4} - \frac{x^{2}}{2} + C_{1} x + C_{2}$ $u = \frac{x^{2}}{2} \ln x - \frac{3 x^{2}}{4} + C_{1} x + C_{2}$ $y = (\frac{x^{2}}{2} \ln x - \frac{3 x^{2}}{4} + C_{1} x + C_{2}) e^{x}$
	Commented by benjo_mathlover last updated on 22/Oct/20

	$t h a n k y o u$
	Answered by john santu last updated on 27/Oct/20
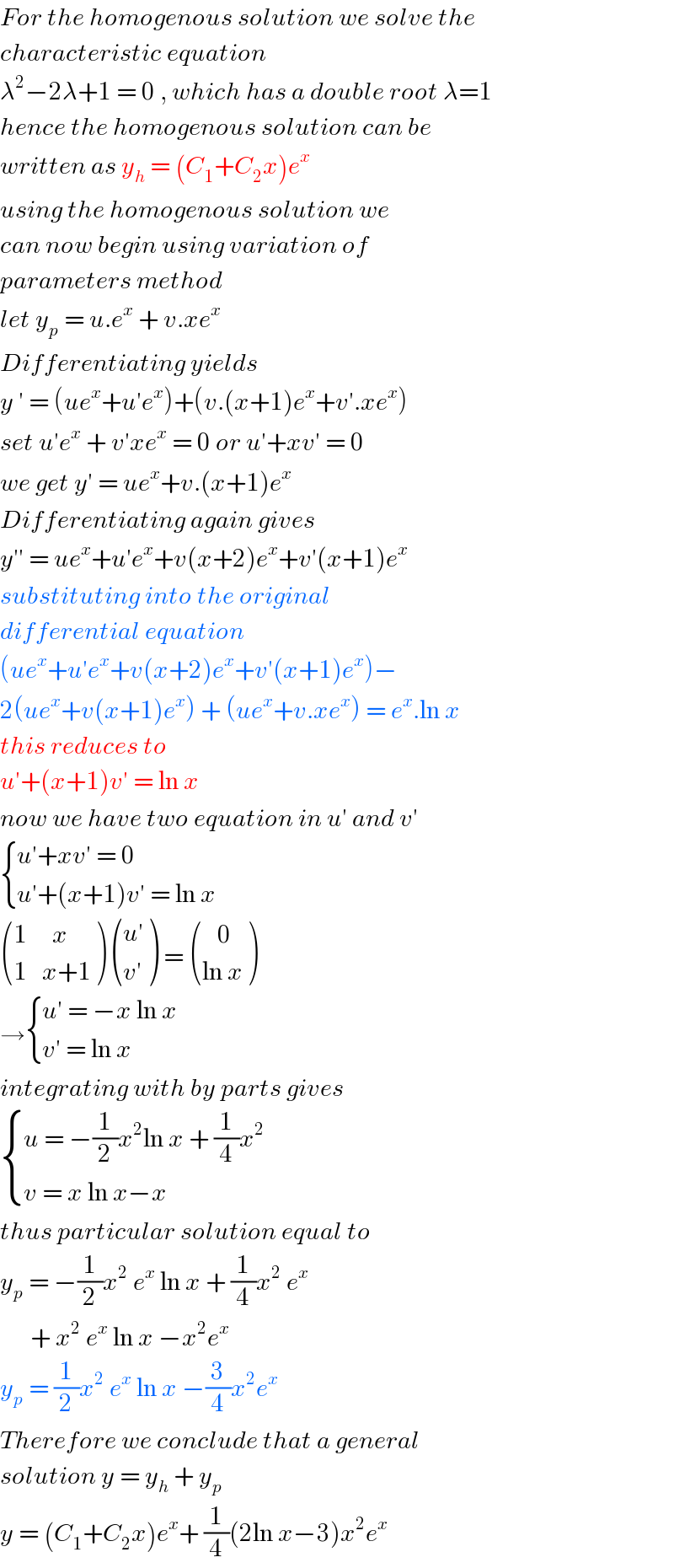
	$For the homogenous solution we solve the characteristic equation λ^2 −2λ+1 = 0 , which has a double root λ=1 hence the homogenous solution can be written as y_h = (C_1 +C_2 x)e^x using the homogenous solution we can now begin using variation of parameters method let y_p = u.e^x + v.xe^x Differentiating yields y ′ = (ue^x +u′e^x )+(v.(x+1)e^x +v′.xe^x ) set u′e^x + v′xe^x = 0 or u′+xv′ = 0 we get y′ = ue^x +v.(x+1)e^x Differentiating again gives y′′ = ue^x +u′e^x +v(x+2)e^x +v′(x+1)e^x substituting into the original differential equation (ue^x +u′e^x +v(x+2)e^x +v′(x+1)e^x )− 2(ue^x +v(x+1)e^x ) + (ue^x +v.xe^x ) = e^x .ln x this reduces to u′+(x+1)v′ = ln x now we have two equation in u′ and v′ { ((u′+xv′ = 0)),((u′+(x+1)v′ = ln x)) :} (((1 x)),((1 x+1)) ) (((u′)),((v′)) ) = ((( 0)),((ln x)) ) → { ((u′ = −x ln x)),((v′ = ln x)) :} integrating with by parts gives { ((u = −(1/2)x^2 ln x + (1/4)x^(2 ) )),((v = x ln x−x )) :} thus particular solution equal to y_p = −(1/2)x^2 e^x ln x + (1/4)x^2 e^x + x^2 e^x ln x −x^2 e^x y_p = (1/2)x^2 e^x ln x −(3/4)x^2 e^x Therefore we conclude that a general solution y = y_h + y_p y = (C_1 +C_2 x)e^x + (1/4)(2ln x−3)x^2 e^x$
	$F o r t h e h o m o g e n o u s s o l u t i o n w e s o l v e t h e$ $c h a r a c t e r i s t i c e q u a t i o n$ $λ^{2} - 2 λ + 1 = 0, w h i c h h a s a d o u b l e r o o t λ = 1$ $h e n c e t h e h o m o g e n o u s s o l u t i o n c a n b e$ $w r i t t e n a s y_{h} = (C_{1} + C_{2} x) e^{x}$ $u s i n g t h e h o m o g e n o u s s o l u t i o n w e$ $c a n n o w b e g i n u s i n g v a r i a t i o n o f$ $p a r a m e t e r s m e t h o d$ $l e t y_{p} = u . e^{x} + v . {x e}^{x}$ $D i f f e r e n t i a t i n g y i e l d s$ $y^{'} = ({u e}^{x} + u^{'} e^{x}) + (v . (x + 1) e^{x} + v^{'} . {x e}^{x})$ $s e t u^{'} e^{x} + v^{'} {x e}^{x} = 0 o r u^{'} + {x v}^{'} = 0$ $w e g e t y^{'} = {u e}^{x} + v . (x + 1) e^{x}$ $D i f f e r e n t i a t i n g a g a i n g i v e s$ $y^{″} = {u e}^{x} + u^{'} e^{x} + v (x + 2) e^{x} + v^{'} (x + 1) e^{x}$ $s u b s t i t u t i n g i n t o t h e o r i g i n a l$ $d i f f e r e n t i a l e q u a t i o n$ $({u e}^{x} + u^{'} e^{x} + v (x + 2) e^{x} + v^{'} (x + 1) e^{x}) -$ $2 ({u e}^{x} + v (x + 1) e^{x}) + ({u e}^{x} + v . {x e}^{x}) = e^{x} . \ln x$ $t h i s r e d u c e s t o$ $u^{'} + (x + 1) v^{'} = \ln x$ $n o w w e h a v e t w o e q u a t i o n i n u^{'} a n d v^{'}$ ${\begin{cases} u^{'} + {x v}^{'} = 0 \\ u^{'} + (x + 1) v^{'} = \ln x \end{cases}$ $(\begin{matrix} 1 x \\ 1 x + 1 \end{matrix}) (\begin{matrix} u^{'} \\ v^{'} \end{matrix}) = (\begin{matrix} 0 \\ \ln x \end{matrix})$ $\to {\begin{cases} u^{'} = - x \ln x \\ v^{'} = \ln x \end{cases}$ $i n t e g r a t i n g w i t h b y p a r t s g i v e s$ ${\begin{cases} u = - \frac{1}{2} x^{2} \ln x + \frac{1}{4} x^{2} \\ v = x \ln x - x \end{cases}$ $t h u s p a r t i c u l a r s o l u t i o n e q u a l t o$ $y_{p} = - \frac{1}{2} x^{2} e^{x} \ln x + \frac{1}{4} x^{2} e^{x}$ $+ x^{2} e^{x} \ln x - x^{2} e^{x}$ $y_{p} = \frac{1}{2} x^{2} e^{x} \ln x - \frac{3}{4} x^{2} e^{x}$ $T h e r e f o r e w e c o n c l u d e t h a t a g e n e r a l$ $s o l u t i o n y = y_{h} + y_{p}$ $y = (C_{1} + C_{2} x) e^{x} + \frac{1}{4} (2 \ln x - 3) x^{2} e^{x}$
	Answered by TANMAY PANACEA last updated on 22/Oct/20

	$P . I = \frac{e^{x} l n x}{{(D - 1)}^{2}} = e^{x} \times \frac{1}{{(D + 1 - 1)}^{2}} \times l n x$ $= \frac{e^{x}}{1} \times \frac{l n x}{D^{2}}$ $\frac{1}{D} \times l n x = x l n x - x$ $\frac{1}{D^{2}} l n x = \int (x l n x - x) d x$ $= l n x \times \frac{x^{2}}{2} - \int \frac{1}{x} \times \frac{x^{2}}{2} d x - \frac{x^{2}}{2}$ $= \frac{x^{2} l n x}{2} - \frac{x^{2}}{4} - \frac{x^{2}}{2}$ $= \frac{x^{2}}{2} (l n x - \frac{1}{2} - 1) = \frac{x^{2}}{2} (\frac{- 3}{2} + l n x)$ $s n s s e r$ $\frac{e^{x} \times x^{2}}{2} o (\frac{- 3}{2} + l n x)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum