Math Question and Answers


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 119136 by Hassen_Timol last updated on 22/Oct/20

Commented by MJS_new last updated on 22/Oct/20

$to understand what happens draw it!$ $use p = 2 \Rightarrow n = 5$ $w^{n} = 1 \Rightarrow draw x - axis (real) and y - axis$ $(imaginary) and a unit circle . then scetch$ $a regular pentagon beginning at (1 / 0)$ $the 2 vertices above the x - axis sum up to$ $S, the ones below sum up to T$ ${it}^{'} s really easy to see; everything else follows$
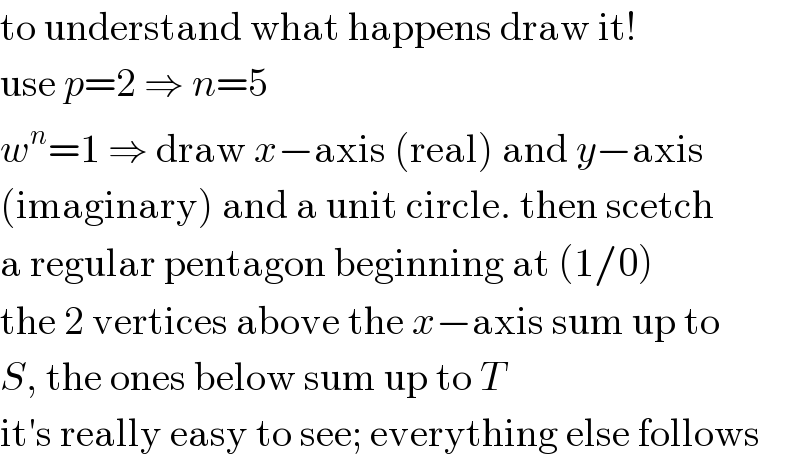
Commented by Hassen_Timol last updated on 22/Oct/20
Okay thank you very much
	Answered by mathmax by abdo last updated on 22/Oct/20
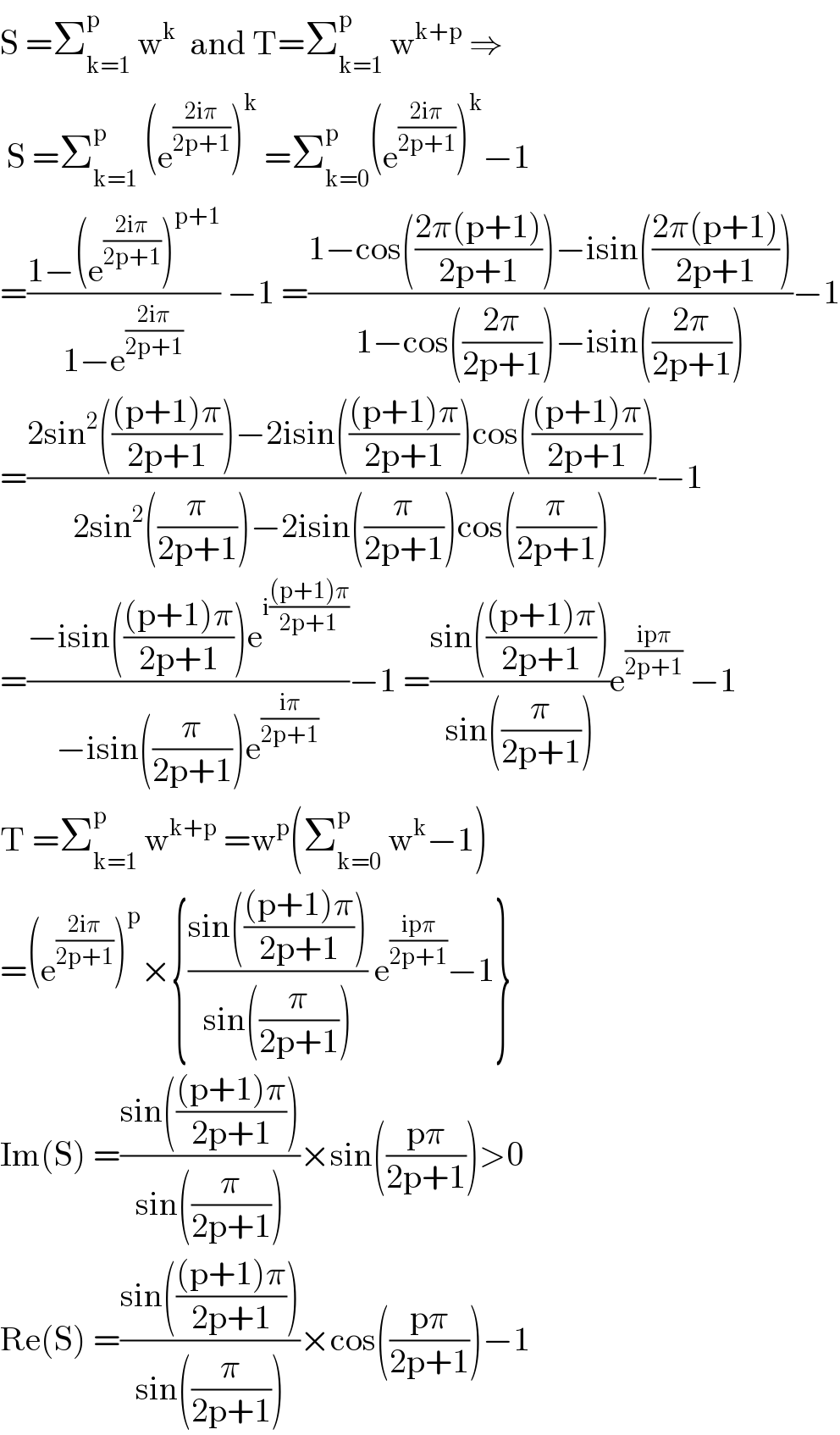
	$S =Σ_(k=1) ^p w^k and T=Σ_(k=1) ^p w^(k+p) ⇒ S =Σ_(k=1) ^p (e^((2iπ)/(2p+1)) )^k =Σ_(k=0) ^p (e^((2iπ)/(2p+1)) )^k −1 =((1−(e^((2iπ)/(2p+1)) )^(p+1) )/(1−e^((2iπ)/(2p+1)) )) −1 =((1−cos(((2π(p+1))/(2p+1)))−isin(((2π(p+1))/(2p+1))))/(1−cos(((2π)/(2p+1)))−isin(((2π)/(2p+1)))))−1 =((2sin^2 ((((p+1)π)/(2p+1)))−2isin((((p+1)π)/(2p+1)))cos((((p+1)π)/(2p+1))))/(2sin^2 ((π/(2p+1)))−2isin((π/(2p+1)))cos((π/(2p+1)))))−1 =((−isin((((p+1)π)/(2p+1)))e^(i(((p+1)π)/(2p+1))) )/(−isin((π/(2p+1)))e^((iπ)/(2p+1)) ))−1 =((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1)))))e^((ipπ)/(2p+1)) −1 T =Σ_(k=1) ^p w^(k+p) =w^p (Σ_(k=0) ^p w^k −1) =(e^((2iπ)/(2p+1)) )^p ×{((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1))))) e^((ipπ)/(2p+1)) −1} Im(S) =((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1)))))×sin(((pπ)/(2p+1)))>0 Re(S) =((sin((((p+1)π)/(2p+1))))/(sin((π/(2p+1)))))×cos(((pπ)/(2p+1)))−1$
	$S = \sum_{k = 1}^{p} w^{k} and T = \sum_{k = 1}^{p} w^{k + p} \Rightarrow$ $S = \sum_{k = 1}^{p} {(e^{\frac{2 i π}{2 p + 1}})}^{k} = \sum_{k = 0}^{p} {(e^{\frac{2 i π}{2 p + 1}})}^{k} - 1$ $= \frac{1 - {(e^{\frac{2 i π}{2 p + 1}})}^{p + 1}}{1 - e^{\frac{2 i π}{2 p + 1}}} - 1 = \frac{1 - \cos (\frac{2 π (p + 1)}{2 p + 1}) - isin (\frac{2 π (p + 1)}{2 p + 1})}{1 - \cos (\frac{2 π}{2 p + 1}) - isin (\frac{2 π}{2 p + 1})} - 1$ $= \frac{{2 \sin}^{2} (\frac{(p + 1) π}{2 p + 1}) - 2 isin (\frac{(p + 1) π}{2 p + 1}) \cos (\frac{(p + 1) π}{2 p + 1})}{{2 \sin}^{2} (\frac{π}{2 p + 1}) - 2 isin (\frac{π}{2 p + 1}) \cos (\frac{π}{2 p + 1})} - 1$ $= \frac{- isin (\frac{(p + 1) π}{2 p + 1}) e^{i \frac{(p + 1) π}{2 p + 1}}}{- isin (\frac{π}{2 p + 1}) e^{\frac{i π}{2 p + 1}}} - 1 = \frac{\sin (\frac{(p + 1) π}{2 p + 1})}{\sin (\frac{π}{2 p + 1})} e^{\frac{ip π}{2 p + 1}} - 1$ $T = \sum_{k = 1}^{p} w^{k + p} = w^{p} (\sum_{k = 0}^{p} w^{k} - 1)$ $= {(e^{\frac{2 i π}{2 p + 1}})}^{p} \times {\frac{\sin (\frac{(p + 1) π}{2 p + 1})}{\sin (\frac{π}{2 p + 1})} e^{\frac{ip π}{2 p + 1}} - 1}$ $Im (S) = \frac{\sin (\frac{(p + 1) π}{2 p + 1})}{\sin (\frac{π}{2 p + 1})} \times \sin (\frac{p π}{2 p + 1}) > 0$ $Re (S) = \frac{\sin (\frac{(p + 1) π}{2 p + 1})}{\sin (\frac{π}{2 p + 1})} \times \cos (\frac{p π}{2 p + 1}) - 1$
	Commented by Hassen_Timol last updated on 26/Oct/20
	Thank you so much you save my entire life
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum