Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 119216 by benjo_mathlover last updated on 23/Oct/20

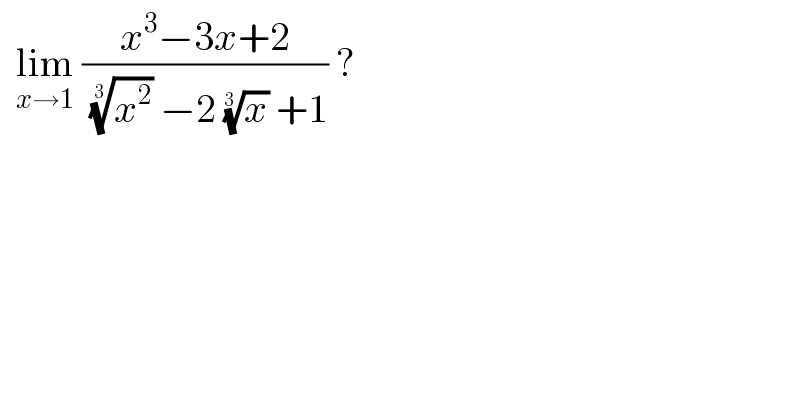
lim_(x→1) ((x^3 −3x+2)/( (x^2 )^(1/(3 )) −2 (x)^(1/(3 )) +1)) ?

$$\:\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{2}}{\:\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} }\:−\mathrm{2}\:\sqrt[{\mathrm{3}\:}]{{x}}\:+\mathrm{1}}\:?\: \\ $$

Commented by MJS_new last updated on 23/Oct/20

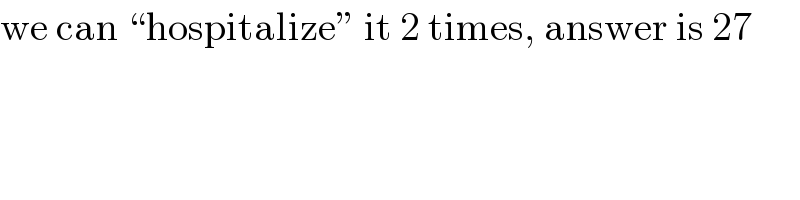
we can “hospitalize” it 2 times, answer is 27

$$\mathrm{we}\:\mathrm{can}\:``\mathrm{hospitalize}''\:\mathrm{it}\:\mathrm{2}\:\mathrm{times},\:\mathrm{answer}\:\mathrm{is}\:\mathrm{27} \\ $$

Commented by benjo_mathlover last updated on 23/Oct/20

yes...

$${yes}... \\ $$

Commented by bemath last updated on 23/Oct/20

without L′Hopital lim_(x→1) (((x−1)(x^2 +x−2))/(((x)^(1/(3 )) −1)^2 )) = lim_(x→1) (((x−1)^2 (x+2))/(((x)^(1/(3 )) −1)^2 )) = 3 × lim_(x→1) [((x−1)/( (x)^(1/(3 )) −1)) ]^2 = 3 × [ lim_(x→1) ((((x)^(1/(3 )) −1)((x^2 )^(1/(3 )) + (x)^(1/(3 )) +1)/( (x)^(1/(3 )) −1)) ]^2 = 3 × (3)^2 = 27

$${without}\:{L}'{Hopital} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{2}} +{x}−\mathrm{2}\right)}{\left(\sqrt[{\mathrm{3}\:}]{{x}}−\mathrm{1}\right)^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{2}\right)}{\left(\sqrt[{\mathrm{3}\:}]{{x}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\:\mathrm{3}\:×\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left[\frac{{x}−\mathrm{1}}{\:\sqrt[{\mathrm{3}\:}]{{x}}−\mathrm{1}}\:\right]^{\mathrm{2}} \\ $$$$=\:\mathrm{3}\:×\:\left[\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left(\sqrt[{\mathrm{3}\:}]{{x}}−\mathrm{1}\right)\left(\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} }\:+\:\sqrt[{\mathrm{3}\:}]{{x}}\:+\mathrm{1}\right.}{\:\sqrt[{\mathrm{3}\:}]{{x}}−\mathrm{1}}\:\right]^{\mathrm{2}} \\ $$$$=\:\mathrm{3}\:×\:\left(\mathrm{3}\right)^{\mathrm{2}} \:=\:\mathrm{27} \\ $$

Commented by malwan last updated on 23/Oct/20

cooool

$${cooool} \\ $$

Answered by benjo_mathlover last updated on 23/Oct/20

let (x)^(1/(3 )) = t lim_(t→1) ((t^9 −3t^3 +2)/(t^2 −2t+1)) = lim_(t→1) ((9t^8 −9t^2 )/(2t−2)) lim_(t→1) ((72t^7 −18t)/2) = 36−9=27

$$\:{let}\:\sqrt[{\mathrm{3}\:}]{{x}}\:=\:{t} \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{t}^{\mathrm{9}} −\mathrm{3}{t}^{\mathrm{3}} +\mathrm{2}}{{t}^{\mathrm{2}} −\mathrm{2}{t}+\mathrm{1}}\:=\:\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{9}{t}^{\mathrm{8}} −\mathrm{9}{t}^{\mathrm{2}} }{\mathrm{2}{t}−\mathrm{2}} \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{72}{t}^{\mathrm{7}} −\mathrm{18}{t}}{\mathrm{2}}\:=\:\mathrm{36}−\mathrm{9}=\mathrm{27} \\ $$

Answered by 1549442205PVT last updated on 23/Oct/20

Put ^3 (√x)=u(x→1∼u→1) lim _(x→1) ((x^3 −3x+2)/( (x^2 )^(1/(3 )) −2 (x)^(1/(3 )) +1)) =lim_(u→1) ((u^9 −3u^3 +2)/(u^2 −2u+1)) ⇔lim_(u→1) (((u^7 +2u^6 +3u^5 +4u^4 +5u^3 +6u^2 +4u+2)(u−1)^2 )/((u−1)^2 )) =lim_(u→1) (u^7 +2u^6 +3u^5 +4u^4 +5u^3 +6u^2 +4u+2) =1+2+3+4+5+6+4+2=27

$$\mathrm{Put}\:\:^{\mathrm{3}} \sqrt{\mathrm{x}}=\mathrm{u}\left(\mathrm{x}\rightarrow\mathrm{1}\sim\mathrm{u}\rightarrow\mathrm{1}\right) \\ $$$$\underset{\mathrm{x}\rightarrow\mathrm{1}} {\:\:\mathrm{lim}\:\:}\frac{{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{2}}{\:\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} }\:−\mathrm{2}\:\sqrt[{\mathrm{3}\:}]{{x}}\:+\mathrm{1}}\:=\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\mathrm{u}^{\mathrm{9}} −\mathrm{3u}^{\mathrm{3}} +\mathrm{2}}{\mathrm{u}^{\mathrm{2}} −\mathrm{2u}+\mathrm{1}} \\ $$$$\Leftrightarrow\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left(\mathrm{u}^{\mathrm{7}} +\mathrm{2u}^{\mathrm{6}} +\mathrm{3u}^{\mathrm{5}} +\mathrm{4u}^{\mathrm{4}} +\mathrm{5u}^{\mathrm{3}} +\mathrm{6u}^{\mathrm{2}} +\mathrm{4u}+\mathrm{2}\right)\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} }{\left(\mathrm{u}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\mathrm{u}^{\mathrm{7}} +\mathrm{2u}^{\mathrm{6}} +\mathrm{3u}^{\mathrm{5}} +\mathrm{4u}^{\mathrm{4}} +\mathrm{5u}^{\mathrm{3}} +\mathrm{6u}^{\mathrm{2}} +\mathrm{4u}+\mathrm{2}\right) \\ $$$$=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{4}+\mathrm{2}=\mathrm{27} \\ $$

Answered by Dwaipayan Shikari last updated on 23/Oct/20

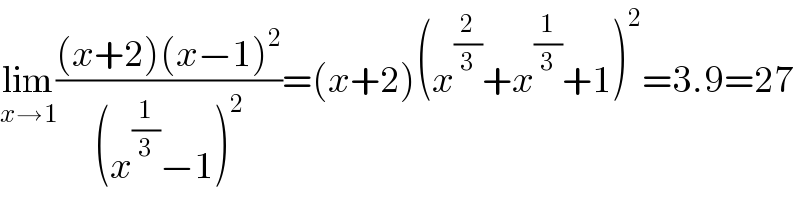
lim_(x→1) (((x+2)(x−1)^2 )/((x^(1/3) −1)^2 ))=(x+2)(x^(2/3) +x^(1/3) +1)^2 =3.9=27

$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{\left({x}+\mathrm{2}\right)\left({x}−\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}\right)^{\mathrm{2}} }=\left({x}+\mathrm{2}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +{x}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}.\mathrm{9}=\mathrm{27} \\ $$

Answered by mathmax by abdo last updated on 24/Oct/20

let f(x)=((x^3 −3x+2)/((^3 (√x))^2 −2(^3 (√x))+1)) we have x^3 −3x+2 =x^3 −x−2x+2 =x(x^2 −1)−2(x−1) =x(x−1)(x+1)−2(x−1) =(x−1)(x^2 +x−2) and (^3 (√x))^2 −2(^3 (√x))+1 =(^3 (√x)−1)^2 ⇒f(x)=(((x−1)(x^2 +x−2))/((^3 (√x)−1)^2 )) we do the changement^3 (√x)−1=t ⇒^3 (√x)=t+1 ⇒x=(t+1)^3 ⇒ (x→1 ⇒t→0) ⇒f(x)=f((t+1)^3 )= =((((t+1)^3 −1)((t+1)^6 +(t+1)^3 −2))/t^2 ) =(((t^3 +3t^2 +3t)((t+1)^6 +(t+1)^2 −2))/t^2 ) =(((t^2 +3t+3)((t+1)^6 +(t+1)^3 −2))/t) we have (t+1)^6 +(t+1)^3 −2 =Σ_(k=0) ^6 C_6 ^k x^k +t^3 +3t^2 +3t −1 =1+C_6 ^1 t +C_6 ^2 t^2 +C_6 ^3 t^3 +C_6 ^4 t^4 +C_6 ^5 t^5 +t^6 +t^3 +3t^2 +3t−1 =9t +(3+C_6 ^2 )t^2 +(1+C_6 ^3 )t^3 +C_6 ^4 t^4 +C_6 ^5 t^5 +t^(6 ) ⇒ f((t+1)^3 ) =(t^3 +3t^2 +3)(9 +(3+C_6 ^2 )t +(1+C_6 ^3 )t^2 +...+t^5 )→3×9=27 ⇒lim_(x→1) f(x)=27

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{3x}+\mathrm{2}}{\left(^{\mathrm{3}} \sqrt{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}\left(^{\mathrm{3}} \sqrt{\mathrm{x}}\right)+\mathrm{1}}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{x}^{\mathrm{3}} −\mathrm{3x}+\mathrm{2}\:=\mathrm{x}^{\mathrm{3}} −\mathrm{x}−\mathrm{2x}+\mathrm{2}\:=\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right) \\ $$$$=\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}+\mathrm{1}\right)−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)\:=\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)\:\mathrm{and} \\ $$$$\left(^{\mathrm{3}} \sqrt{\mathrm{x}}\right)^{\mathrm{2}} −\mathrm{2}\left(^{\mathrm{3}} \sqrt{\mathrm{x}}\right)+\mathrm{1}\:=\left(^{\mathrm{3}} \sqrt{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} \:\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{2}\right)}{\left(^{\mathrm{3}} \sqrt{\mathrm{x}}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:^{\mathrm{3}} \sqrt{\mathrm{x}}−\mathrm{1}=\mathrm{t}\:\Rightarrow^{\mathrm{3}} \sqrt{\mathrm{x}}=\mathrm{t}+\mathrm{1}\:\Rightarrow\mathrm{x}=\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} \:\Rightarrow \\ $$$$\left(\mathrm{x}\rightarrow\mathrm{1}\:\Rightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} \right)= \\ $$$$=\frac{\left(\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{1}\right)\left(\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{6}} +\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{2}\right)}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{t}^{\mathrm{3}} +\mathrm{3t}^{\mathrm{2}} +\mathrm{3t}\right)\left(\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{6}} +\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\right)}{\mathrm{t}^{\mathrm{2}} } \\ $$$$=\frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{3t}+\mathrm{3}\right)\left(\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{6}} +\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{2}\right)}{\mathrm{t}}\:\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{6}} +\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} −\mathrm{2}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{6}} \:\mathrm{C}_{\mathrm{6}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:+\mathrm{t}^{\mathrm{3}} +\mathrm{3t}^{\mathrm{2}} \:+\mathrm{3t}\:−\mathrm{1} \\ $$$$=\mathrm{1}+\mathrm{C}_{\mathrm{6}} ^{\mathrm{1}} \:\mathrm{t}\:+\mathrm{C}_{\mathrm{6}} ^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} +\mathrm{C}_{\mathrm{6}} ^{\mathrm{3}} \mathrm{t}^{\mathrm{3}} \:+\mathrm{C}_{\mathrm{6}} ^{\mathrm{4}} \:\mathrm{t}^{\mathrm{4}} +\mathrm{C}_{\mathrm{6}} ^{\mathrm{5}} \:\mathrm{t}^{\mathrm{5}} \:+\mathrm{t}^{\mathrm{6}} +\mathrm{t}^{\mathrm{3}} \:+\mathrm{3t}^{\mathrm{2}} \:+\mathrm{3t}−\mathrm{1} \\ $$$$=\mathrm{9t}\:+\left(\mathrm{3}+\mathrm{C}_{\mathrm{6}} ^{\mathrm{2}} \right)\mathrm{t}^{\mathrm{2}} \:+\left(\mathrm{1}+\mathrm{C}_{\mathrm{6}} ^{\mathrm{3}} \right)\mathrm{t}^{\mathrm{3}} \:+\mathrm{C}_{\mathrm{6}} ^{\mathrm{4}} \mathrm{t}^{\mathrm{4}} +\mathrm{C}_{\mathrm{6}} ^{\mathrm{5}} \mathrm{t}^{\mathrm{5}} +\mathrm{t}^{\mathrm{6}\:} \Rightarrow \\ $$$$\mathrm{f}\left(\left(\mathrm{t}+\mathrm{1}\right)^{\mathrm{3}} \right)\:=\left(\mathrm{t}^{\mathrm{3}} +\mathrm{3t}^{\mathrm{2}} +\mathrm{3}\right)\left(\mathrm{9}\:+\left(\mathrm{3}+\mathrm{C}_{\mathrm{6}} ^{\mathrm{2}} \right)\mathrm{t}\:+\left(\mathrm{1}+\mathrm{C}_{\mathrm{6}} ^{\mathrm{3}} \right)\mathrm{t}^{\mathrm{2}} +...+\mathrm{t}^{\mathrm{5}} \right)\rightarrow\mathrm{3}×\mathrm{9}=\mathrm{27} \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{1}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{27} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com