Find all sum of all x interval [ 0, 2π ] such that 3cot^2 x + 8 cot x + 3 = 0


Question and Answers Forum

All Questions Topic List
Trigonometry Questions
Previous in All Question Next in All Question
Previous in Trigonometry Next in Trigonometry
Question Number 119373 by bobhans last updated on 24/Oct/20

$F i n d a l l s u m o f a l l x i n t e r v a l$ $[0, 2 π] s u c h t h a t 3 \cot^{2} x + 8 \cot x + 3 = 0$
Commented by benjo_mathlover last updated on 24/Oct/20

$c o n s i d e r t h e q u a d r a t i c e q u a t i o n$ $3 q^{2} + 8 q + 3 = 0, w i t h t h e r o o t s a r e q_{1} = \frac{- 8 + 2 \sqrt{7}}{6}$ $a n d q_{2} = \frac{- 8 - 2 \sqrt{7}}{6} . b o t h r o o t s a r e r e a l a n d$ $t h e i r p r o d u c t e q u a l t o - 1 . B e c a u s e y = \cot x i s a b i j e c t i o n$ $f r o m t h e i n t e r v a l (0, π) t o t h e r e a l n u m b e r, t h e r e$ $i s a u n i q u e p a i r o f n u m b e r s x_{1.1} a n d x_{2.1}$ $w i t h 0 < x_{1.1}, x_{2.1} < π s u c h t h a t \cot x_{1.1} = q_{1}$ $a n d \cot x_{2.1} = q_{2} . B e c a u s e q_{1} a n d q_{2} a r e$ $n e g a t i v e, \frac{π}{2} < x_{1.1}, x_{2.1} < π a n d s o$ $π < x_{1.1}, x_{2.1} < 2 π . S i n c e \tan x \cot x = 1$ $b o t h \tan x a n d \cot x h a v e p e r i o d π, i t f o l l o w s t h a t$ $1 = \tan x \cot x = \cot x \cot (\frac{π}{2} - x) = \cot x \cot (\frac{3 π}{2} - x)$ $1 = \cot x_{1.1} . \cot x_{2.1} t h e n x_{1.1} + x_{2.1} = \frac{3 π}{2}$ $l i k e w i s e i n i n t e r v a l (π, 2 π) t h e r e i s u n i q u e$ $p a i r n u m b e r x_{1.2} a n d x_{2.2} s a t i s f y i n g t h e$ $c o n d i t i o n s o f t h e p r o b l e m w i t h x_{1.2} + x_{2.2} = \frac{7 π}{2}$ $T h e r e f o r e x_{1.1} + x_{2.1} + x_{1.2} + x_{2.2} = \frac{3 π}{2} + \frac{7 π}{2} = 5 π$
	Answered by TANMAY PANACEA last updated on 24/Oct/20

	$t a n x = a$ $\frac{3}{a^{2}} + \frac{8}{a} + 3 = 0$ $3 + 8 a + 3 a^{2} = 0$ $a = \frac{- 8 \pm \sqrt{8^{2} - 4 \times 3 \times 3}}{2 \times 3} = \frac{- 8 \pm 2 \sqrt{7}}{2 \times 3} = \frac{- 4 \pm \sqrt{7}}{3}$ ${t a n x}_{1} = \frac{- 4 + \sqrt{7}}{3} = t a n α {t a n x}_{2} = \frac{- 4 - \sqrt{7}}{3} = t a n β$ $t a n (α + β) = \frac{t a n α + t a n β}{1 - t a n α t a n β} = \frac{\frac{- 8}{3}}{1 - (\frac{16 - 7}{9})} = t a n \frac{π}{2}$ $(α + β) = \frac{π}{2}$ $t a n (α + β) = t a n \frac{π}{2} = t a n (π + \frac{π}{2}) = t a n \frac{3 π}{2}$ $t a n α = t a n (π + α)$ $t a n β = t a n (π + β)$ $α + (α + π) + β + (β + π) + (α + β) + (π + α + β)$ $= 4 (α + β) + 3 π$ $= 4 (\frac{π}{2}) + 3 π = 5 π$
	Commented by 1549442205PVT last updated on 24/Oct/20

	$Sir mistake at place \sqrt{8^{2} - 4 \times 3 \times 3}$ $= \sqrt{28} = 2 \sqrt{7}$
	Commented by TANMAY PANACEA last updated on 24/Oct/20

	$y e s s i r c o r r e c t e d$
	Answered by MJS_new last updated on 24/Oct/20

	${3 \cot}^{2} x + 8 \cot x + 3 = 0$ $\frac{{3 \cos}^{2} x}{\sin^{2} x} + \frac{8 \cos x}{\sin x} + 3 = 0$ $\frac{{3 \cos}^{2} + 8 \cos x \sin x + {3 \sin}^{2} x}{\sin^{2} x} = 0$ $3 + 8 \cos x \sin x = 0$ $\cos x \sin x = - \frac{3}{8}$ $\frac{1}{2} \sin 2 x = - \frac{3}{8}$ $\sin 2 x = - \frac{3}{4}$ $x = n π - \frac{1}{2} \arcsin \frac{3}{4} \lor x = n π + \frac{π}{2} + \frac{1}{2} \arcsin \frac{3}{4}$ $let α = \frac{1}{2} \arcsin \frac{3}{4}$ $for 0 ⩽ x < 2 π we get$ $x = π - α \lor x = 2 π - α \lor x = \frac{π}{2} + α \lor x = \frac{3 π}{2} + α$ $\Rightarrow sum of these is 5 π$
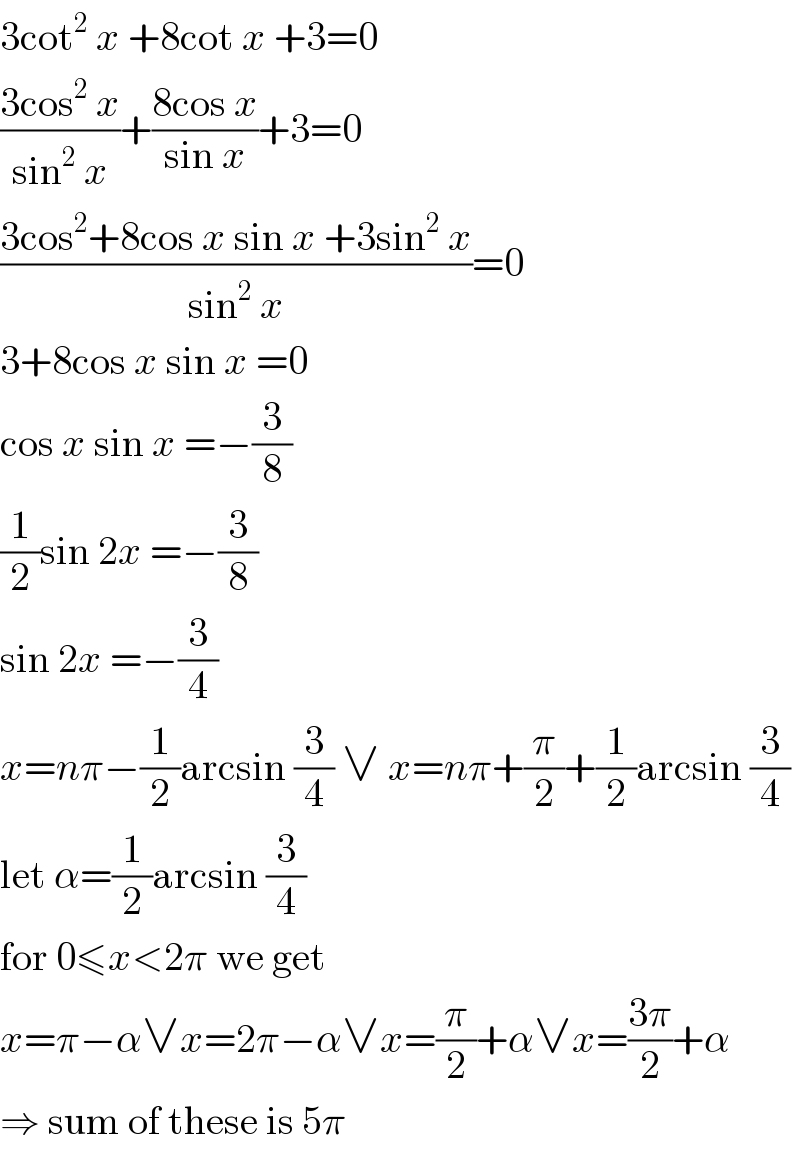
	Answered by 1549442205PVT last updated on 24/Oct/20
	$3cot^2 x + 8 cot x + 3 = 0 Δ′=4^2 −9=7⇒cotx=((−4±(√7))/3) ⇒tanx=(3/(−4±(√7)))=((3(−4∓(√7)))/9)=((−4∓(√7))/3) Put α=tan^(−1) (((−4+(√7))/3)),β=tan^(−1) (((−4−(√7))/3)) α≈−24°17′42”,β≈−65°42′17” Since α,β∈[0,2π] and tanx=tan(x+kπ) we get α∈{155°42′17”,335°42′17”} β∈{114°17′43”,294°17′43”} ⇒α_1 +α_2 +β_1 +β_2 =900° Thus,Sum of all the angles satisfying given equation equal to 900°$
	$3 \cot^{2} x + 8 \cot x + 3 = 0$ $Δ^{'} = 4^{2} - 9 = 7 \Rightarrow cotx = \frac{- 4 \pm \sqrt{7}}{3}$ $\Rightarrow tanx = \frac{3}{- 4 \pm \sqrt{7}} = \frac{3 (- 4 \mp \sqrt{7})}{9} = \frac{- 4 \mp \sqrt{7}}{3}$ $Put α = \tan^{- 1} (\frac{- 4 + \sqrt{7}}{3}), β = \tan^{- 1} (\frac{- 4 - \sqrt{7}}{3})$ $α \approx - 24 ° 17^{'} 42^{″}, β \approx - 65 ° 42^{'} 17^{″}$ $Since α, β \in [0, 2 π] and tanx = \tan (x + k π)$ $we get α \in {155 ° 42^{'} 17^{″}, 335 ° 42^{'} 17^{″}}$ $β \in {114 ° 17^{'} 43^{″}, 294 ° 17^{'} 43^{″}}$ $\Rightarrow α_{1} + α_{2} + β_{1} + β_{2} = 900 °$ $Thus, Sum of all the angles satisfying$ $given equation equal to 900 °$
	Answered by Bird last updated on 24/Oct/20

	$3 {c o t a n}^{2} x + 8 c o t a n x + 3 = 0 \Rightarrow$ $\frac{3}{{t a n}^{2} x} + \frac{8}{t a n x} + 3 = 0 \Rightarrow$ $3 + 8 t a n x + 3 {t a n}^{2} x = 0 \Rightarrow$ $3 {t a n}^{2} x + 8 t a n x + 3 = 0$ $t a n x = u \Rightarrow 3 u^{2} + 8 u + 3 = 0$ $Δ^{^{'}} = 4^{2} - 9 = 16 - 9 = 7 \Rightarrow$ $u_{1} = \frac{- 4 + \sqrt{7}}{3} a n d u_{2} = \frac{- 4 - \sqrt{7}}{3}$ $t a n x = \frac{- 4 + \sqrt{7}}{3} \Rightarrow x = a r c t a n (\frac{- 4 + \sqrt{7}}{3}) + n π$ $t a n x = \frac{- 4 - \sqrt{7}}{3} \Rightarrow x = - a r c t a n (\frac{4 + \sqrt{7}}{3}) + n π$ $(n \in Z)$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum