
Question and Answers Forum
Question Number 119421 by bemath last updated on 24/Oct/20
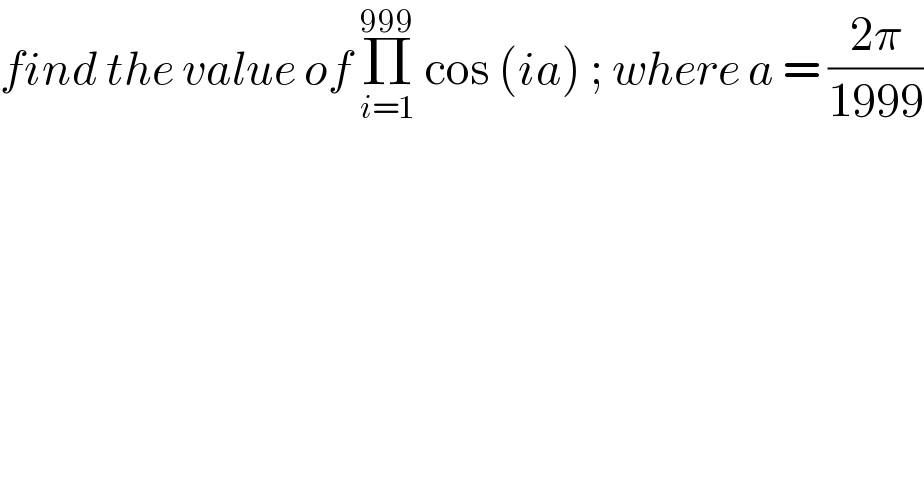
Commented by MJS_new last updated on 24/Oct/20
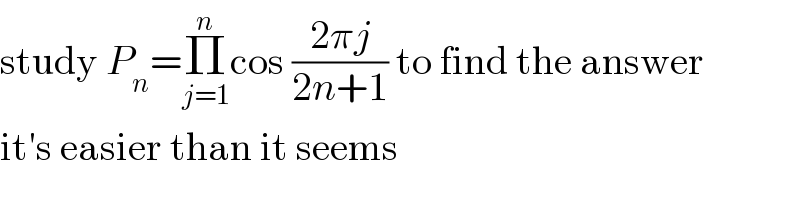
Answered by benjo_mathlover last updated on 24/Oct/20

Answered by mindispower last updated on 24/Oct/20
![Π_(i=1) ^m cos(i((2π)/(2m+1))) Z^(2m+1) −1=0⇒Z=e^((2ikπ)/(2m+1)) ,k∈[0,2m] z^(2m+1) −1=Π_(k≤2m) (z−e^((2ikπ)/(2m+1)) ) z=−1⇒ −2=Π_(k=0) ^(2m) (−1−e^((2ikπ)/(2m+1)) )=−1e^(i(π/(2m+1)).((2m(2m+1))/2)) .Π_(k≤2m) (2cos(((kπ)/(2m+1))) =(−1)^(m+1) 2^(2m+1) Π_(k≤2m) cos(((kπ)/(2m+1))) Π_(k≤2m) cos(((kπ)/(2m+1)))=Π_(k≤m) cos(((kπ)/(2m+1))).Π_(m<k≤2m) (−cos(π−((kπ)/(2m+1)))) put k→2m+1−k in2nd ⇒ =Π_(1≤k≤m) cos(((kπ)/(2m+1))).(−1)^m .Π_(k≤m) cos(((π(2m+1)−(2m+1−k)π)/(2m+1)) =(−1)^m (Π_(k=1) ^m cos(((kπ)/(2m+1))))^2 ⇒−2=(−1)^(m+1) .2^(2m+1) .(−1)^m .(Π_(k≤m) cos(((kπ)/(2m+1))))^2 ⇒(1/2^(2m) )=Π_(k≤m) cos^2 (((kπ)/(2m+1))) since0<((kπ)/(2m+1))<((mπ)/(2m))=(π/2) ⇒Π_(k≤m) cos(((kπ)/(2m+1)))=(1/2^m ) put m=999⇒Π_(k≤999) cos(((kπ)/(1999)))=(1/2^(999) )](Q119443.png)
| ||
Question and Answers Forum | ||
Question Number 119421 by bemath last updated on 24/Oct/20 | ||
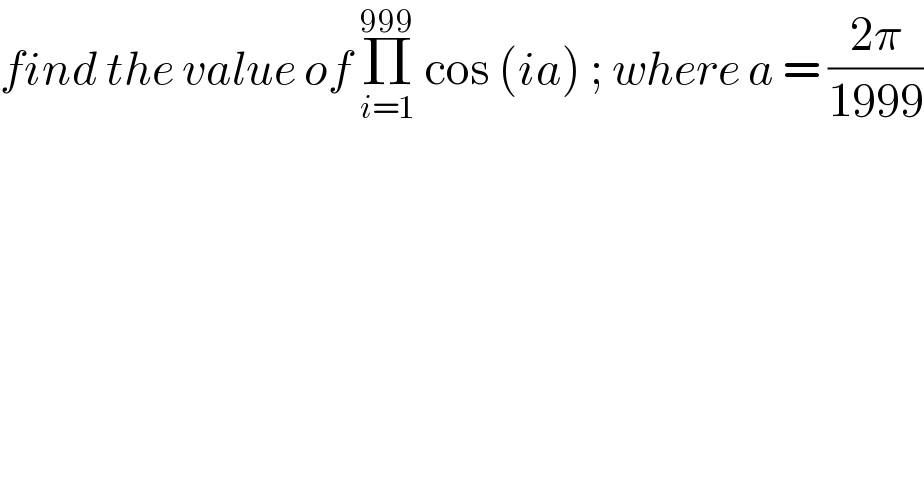 | ||
Commented by MJS_new last updated on 24/Oct/20 | ||
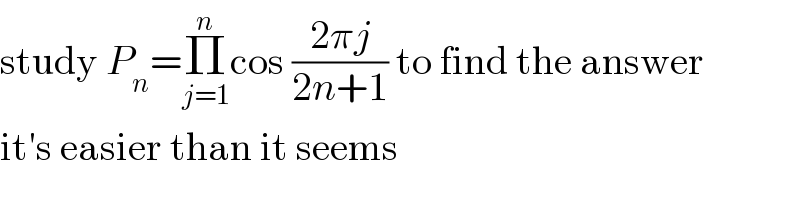 | ||
Answered by benjo_mathlover last updated on 24/Oct/20 | ||
 | ||
| ||
Answered by mindispower last updated on 24/Oct/20 | ||
![Π_(i=1) ^m cos(i((2π)/(2m+1))) Z^(2m+1) −1=0⇒Z=e^((2ikπ)/(2m+1)) ,k∈[0,2m] z^(2m+1) −1=Π_(k≤2m) (z−e^((2ikπ)/(2m+1)) ) z=−1⇒ −2=Π_(k=0) ^(2m) (−1−e^((2ikπ)/(2m+1)) )=−1e^(i(π/(2m+1)).((2m(2m+1))/2)) .Π_(k≤2m) (2cos(((kπ)/(2m+1))) =(−1)^(m+1) 2^(2m+1) Π_(k≤2m) cos(((kπ)/(2m+1))) Π_(k≤2m) cos(((kπ)/(2m+1)))=Π_(k≤m) cos(((kπ)/(2m+1))).Π_(m<k≤2m) (−cos(π−((kπ)/(2m+1)))) put k→2m+1−k in2nd ⇒ =Π_(1≤k≤m) cos(((kπ)/(2m+1))).(−1)^m .Π_(k≤m) cos(((π(2m+1)−(2m+1−k)π)/(2m+1)) =(−1)^m (Π_(k=1) ^m cos(((kπ)/(2m+1))))^2 ⇒−2=(−1)^(m+1) .2^(2m+1) .(−1)^m .(Π_(k≤m) cos(((kπ)/(2m+1))))^2 ⇒(1/2^(2m) )=Π_(k≤m) cos^2 (((kπ)/(2m+1))) since0<((kπ)/(2m+1))<((mπ)/(2m))=(π/2) ⇒Π_(k≤m) cos(((kπ)/(2m+1)))=(1/2^m ) put m=999⇒Π_(k≤999) cos(((kπ)/(1999)))=(1/2^(999) )](Q119443.png) | ||
| ||