Question Number 119462 by mnjuly1970 last updated on 24/Oct/20
$$\:\:\:\:\:\:\:\:\:\:...\:{advanced}\:{calculus}... \\ $$$$\:\:\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{tan}^{−\mathrm{1}} \left({x}\right)}{{e}^{\mathrm{2}\pi{x}} −\mathrm{1}}{dx}\:=? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}.{n}.\mathrm{1970} \\ $$
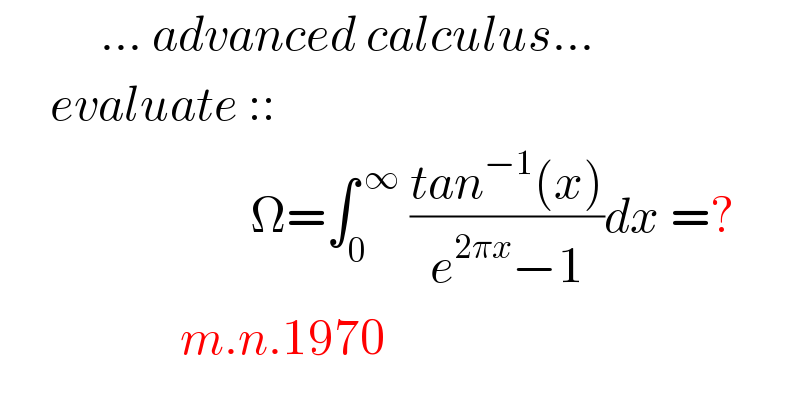
Answered by mathmax by abdo last updated on 25/Oct/20
![let take a try with series A =∫_0 ^∞ ((arctanx)/(e^(2πx) −1))dx ⇒A =∫_0 ^∞ ((e^(−2πx) arctanx)/(1−e^(−2πx) ))dx =∫_0 ^∞ e^(−2πx) arctanxΣ_(n=0) ^∞ e^(−2nπx) dx =Σ_(n=0) ^∞ ∫_0 ^∞ e^(−2π(n+1)x) arctanx dx =Σ_(n=0) ^∞ A_n A_n =∫_0 ^∞ e^(−2π(n+1)x) arctanx dx =_(by parts) [−(e^(−2π(n+1)x) /(2π(n+1))) arctanx]_0 ^∞ +∫_0 ^∞ (e^(−2π(n+1)x) /(2π(n+1)))×(dx/(1+x^2 )) =(1/(2π(n+1)))∫_0 ^∞ (e^(−2π(n+1)x) /(1+x^2 ))dx =_(2π(n+1)x=t) (1/(2π(n+1)))∫_0 ^∞ (e^(−t) /(1+(t^2 /(4π^2 (n+1)^2 ))))×(dt/(2π(n+1))) =(1/(4π^2 (n+1)^2 )) ∫_0 ^∞ (e^(−t) /(t^2 +4π^2 (n+1)^2 ))×4π^2 (n+1)^2 dt =∫_0 ^∞ (e^(−t) /(t^2 +4π^2 (n+1)^2 ))dt =∫_0 ^∞ (1/(t^2 +4π^2 (n+1)^2 ))(Σ_(p=0) ^∞ (((−t)^p )/(p!)))dt =Σ_(p=0) ^∞ (((−1)^p )/(p!))∫_0 ^∞ (t^p /(t^2 +4π^2 (n+1)^2 ))dt....be continued...](Q119502.png)
$$\mathrm{let}\:\mathrm{take}\:\mathrm{a}\:\mathrm{try}\:\mathrm{with}\:\mathrm{series} \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{arctanx}}{\mathrm{e}^{\mathrm{2}\pi\mathrm{x}} −\mathrm{1}}\mathrm{dx}\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{2}\pi\mathrm{x}} \mathrm{arctanx}}{\mathrm{1}−\mathrm{e}^{−\mathrm{2}\pi\mathrm{x}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2}\pi\mathrm{x}} \mathrm{arctanx}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{2n}\pi\mathrm{x}} \mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \:\mathrm{arctanx}\:\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{A}_{\mathrm{n}} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \mathrm{arctanx}\:\mathrm{dx} \\ $$$$=_{\mathrm{by}\:\mathrm{parts}} \:\:\:\left[−\frac{\mathrm{e}^{−\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} }{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\:\mathrm{arctanx}\right]_{\mathrm{0}} ^{\infty} +\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} }{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}×\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=_{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}=\mathrm{t}} \frac{\mathrm{1}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} }{\mathrm{1}+\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }}×\frac{\mathrm{dt}}{\mathrm{2}\pi\left(\mathrm{n}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} +\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }×\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} +\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} +\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\left(\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{t}\right)^{\mathrm{p}} }{\mathrm{p}!}\right)\mathrm{dt} \\ $$$$=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{\mathrm{p}} }{\mathrm{p}!}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\mathrm{p}} }{\mathrm{t}^{\mathrm{2}} \:+\mathrm{4}\pi^{\mathrm{2}} \left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt}....\mathrm{be}\:\mathrm{continued}... \\ $$
Answered by mindispower last updated on 25/Oct/20
![Abel plana formula Σ_(m≥0) f(m)=∫_0 ^∞ f(x)dx+((f(0))/2)+i∫_0 ^∞ ((f(it)−f(−it))/(e^(2πt) −1))dt f(x)=(1/((x+z)^2 ))⇒ Σ_(n≥0) (1/((n+z)^2 ))=∫^∞ _0 (1/((x+z)^2 ))dx+(1/(2z^2 ))+i∫_0 ^∞ (((1/((it+z)^2 ))−(1/((−it+z)^2 )))/(e^(2πt) −1))dt =(1/z)+(1/(2z^2 ))+i∫_0 ^∞ ((−4itz)/((z^2 +t^2 )^2 (e^(2πt) −1)))dt =(1/z)+(1/(2z^2 ))+2∫_0 ^∞ ((2tz)/((z^2 +t^2 )^2 (e^(2πt) −1)))dt Σ_(n≥0) (1/((n+z)^2 ))=Ψ′(z)=(lnΓ(z))′′ we have ln(Γ(z))′′=(1/z)+(1/(2z^2 ))+2∫_0 ^∞ ((2tz)/((z^2 +t^2 )^2 (e^(2πt) −1)))dt by integrate ⇒ln(Γ(z))′=ln(z)−(1/(2z))+2∫_0 ^∞ −(t/((z^2 +t^2 ))).(dt/((e^(2πt) −1)))+c ln(Γ(z))=zln(z)−z−(1/2)ln(z)−2∫_0 ^∞ ∫(t/(z^2 +t^2 ))dz.(dt/(e^(2πt) −1))+cz+c′ =(z−(1/2))ln(z)+(c−1)z+2∫_0 ^∞ ((arctan((t/z)))/(e^(2πt) −1))dt+c′ ⇒[log(Γ(z))−(z−(1/2))ln(z)−(c−1)z−c′]=2∫((arctan((t/z)))/(e^(2πt) −1)) when z→∞?we muste have 0 bothe side ⇒c=′((log(2π))/2),c=0“striling formula for Γ(z)” ⇔ log(Γ(z))=(z−(1/2))ln(z)−z+((log(2π))/2)+2∫_0 ^∞ ((tan^(−1) ((t/z)))/(e^(2πt) −1))dt for z=1 ⇒log(Γ(1))=−1+((log(2π))/2)+2∫_0 ^∞ ((tan^(−1) (t))/(e^(2πt) −1))dt ⇒∫_0 ^∞ ((tan^(−1) (t))/(e^(2πt) −1))dt=((2−log(2π))/4)](Q119555.png)
$${Abel}\:{plana}\:{formula} \\ $$$$\underset{{m}\geqslant\mathrm{0}} {\sum}{f}\left({m}\right)=\int_{\mathrm{0}} ^{\infty} {f}\left({x}\right){dx}+\frac{{f}\left(\mathrm{0}\right)}{\mathrm{2}}+{i}\int_{\mathrm{0}} ^{\infty} \frac{{f}\left({it}\right)−{f}\left(−{it}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\left({x}+{z}\right)^{\mathrm{2}} }\Rightarrow \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+{z}\right)^{\mathrm{2}} }=\underset{\mathrm{0}} {\int}^{\infty} \frac{\mathrm{1}}{\left({x}+{z}\right)^{\mathrm{2}} }{dx}+\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }+{i}\int_{\mathrm{0}} ^{\infty} \frac{\frac{\mathrm{1}}{\left({it}+{z}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(−{it}+{z}\right)^{\mathrm{2}} }}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt} \\ $$$$=\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }+{i}\int_{\mathrm{0}} ^{\infty} \frac{−\mathrm{4}{itz}}{\left({z}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left({e}^{\mathrm{2}\pi{t}} −\mathrm{1}\right)}{dt} \\ $$$$=\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{tz}}{\left({z}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left({e}^{\mathrm{2}\pi{t}} −\mathrm{1}\right)}{dt} \\ $$$$\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({n}+{z}\right)^{\mathrm{2}} }=\Psi'\left({z}\right)=\left({ln}\Gamma\left({z}\right)\right)'' \\ $$$${we}\:{have} \\ $$$${ln}\left(\Gamma\left({z}\right)\right)''=\frac{\mathrm{1}}{{z}}+\frac{\mathrm{1}}{\mathrm{2}{z}^{\mathrm{2}} }+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{tz}}{\left({z}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left({e}^{\mathrm{2}\pi{t}} −\mathrm{1}\right)}{dt} \\ $$$${by}\:{integrate} \\ $$$$\Rightarrow{ln}\left(\Gamma\left({z}\right)\right)'={ln}\left({z}\right)−\frac{\mathrm{1}}{\mathrm{2}{z}}+\mathrm{2}\int_{\mathrm{0}} ^{\infty} −\frac{{t}}{\left({z}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)}.\frac{{dt}}{\left({e}^{\mathrm{2}\pi{t}} −\mathrm{1}\right)}+{c} \\ $$$${ln}\left(\Gamma\left({z}\right)\right)={zln}\left({z}\right)−{z}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({z}\right)−\mathrm{2}\int_{\mathrm{0}} ^{\infty} \int\frac{{t}}{{z}^{\mathrm{2}} +{t}^{\mathrm{2}} }{dz}.\frac{{dt}}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}+{cz}+{c}' \\ $$$$=\left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left({z}\right)+\left({c}−\mathrm{1}\right){z}+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left(\frac{{t}}{{z}}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt}+{c}' \\ $$$$\Rightarrow\left[{log}\left(\Gamma\left({z}\right)\right)−\left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left({z}\right)−\left({c}−\mathrm{1}\right){z}−{c}'\right]=\mathrm{2}\int\frac{{arctan}\left(\frac{{t}}{{z}}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}} \\ $$$${when}\:{z}\rightarrow\infty?{we}\:{muste}\:{have}\:\mathrm{0}\:{bothe}\:{side} \\ $$$$\Rightarrow{c}='\frac{{log}\left(\mathrm{2}\pi\right)}{\mathrm{2}},{c}=\mathrm{0}``{striling}\:{formula}\:{for}\:\Gamma\left({z}\right)'' \\ $$$$\Leftrightarrow \\ $$$${log}\left(\Gamma\left({z}\right)\right)=\left({z}−\frac{\mathrm{1}}{\mathrm{2}}\right){ln}\left({z}\right)−{z}+\frac{{log}\left(\mathrm{2}\pi\right)}{\mathrm{2}}+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\frac{{t}}{{z}}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt} \\ $$$${for}\:{z}=\mathrm{1} \\ $$$$\Rightarrow{log}\left(\Gamma\left(\mathrm{1}\right)\right)=−\mathrm{1}+\frac{{log}\left(\mathrm{2}\pi\right)}{\mathrm{2}}+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left({t}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{tan}^{−\mathrm{1}} \left({t}\right)}{{e}^{\mathrm{2}\pi{t}} −\mathrm{1}}{dt}=\frac{\mathrm{2}−{log}\left(\mathrm{2}\pi\right)}{\mathrm{4}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 25/Oct/20
$${peace}\:{be}\:{upon}\:{you}\:{mr}\:{power} \\ $$$$\:.{super}\:{nice} \\ $$$$\:\:{good}\:{for}\:{you}... \\ $$
Commented by mindispower last updated on 25/Oct/20
$${withe}\:{pleasur} \\ $$