Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 119600 by bemath last updated on 25/Oct/20

Find gcd of x^4 +x^3 −4x^2 +x+5 and x^3 +x^2 −9x−9

$${Find}\:{gcd}\:{of}\:{x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +{x}+\mathrm{5}\: \\ $$$${and}\:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{9} \\ $$

Answered by TANMAY PANACEA last updated on 25/Oct/20

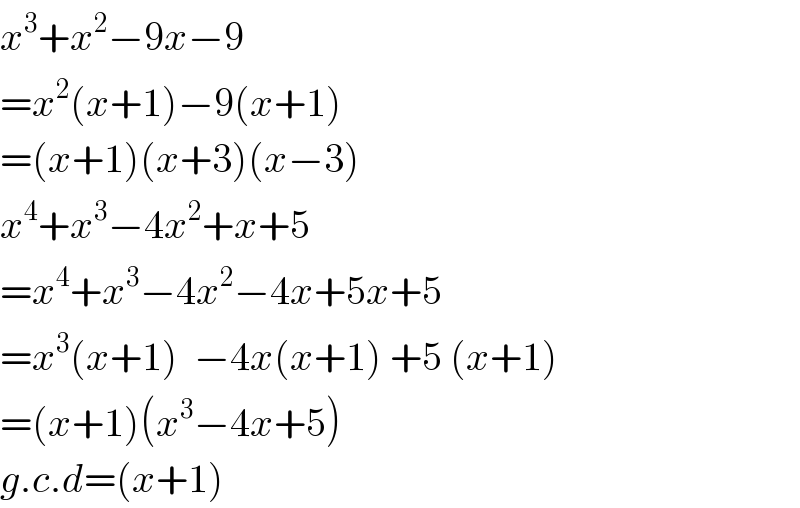
x^3 +x^2 −9x−9 =x^2 (x+1)−9(x+1) =(x+1)(x+3)(x−3) x^4 +x^3 −4x^2 +x+5 =x^4 +x^3 −4x^2 −4x+5x+5 =x^3 (x+1) −4x(x+1) +5 (x+1) =(x+1)(x^3 −4x+5) g.c.d=(x+1)

$${x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{9} \\ $$$$={x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)−\mathrm{9}\left({x}+\mathrm{1}\right) \\ $$$$=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)\left({x}−\mathrm{3}\right) \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +{x}+\mathrm{5} \\ $$$$={x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}{x}+\mathrm{5} \\ $$$$={x}^{\mathrm{3}} \left({x}+\mathrm{1}\right)\:\:−\mathrm{4}{x}\left({x}+\mathrm{1}\right)\:+\mathrm{5}\:\left({x}+\mathrm{1}\right)\:\: \\ $$$$=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{3}} −\mathrm{4}{x}+\mathrm{5}\right) \\ $$$${g}.{c}.{d}=\left({x}+\mathrm{1}\right) \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

to Tinku tara why i can not share question

$${to}\:{Tinku}\:{tara}\:{why}\:{i}\:{can}\:{not}\:{share}\:{question} \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

Commented by TANMAY PANACEA last updated on 25/Oct/20

no share button

$${no}\:{share}\:{button} \\ $$

Commented by bemath last updated on 25/Oct/20

click three dots sir

$${click}\:{three}\:{dots}\:{sir} \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

ok sir

$${ok}\:{sir} \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

∫_0 ^(2π) (dx/(2cos^2 x+(√3) sin^2 x)) i can not post by + so in comment

$$\int_{\mathrm{0}} ^{\mathrm{2}\pi} \frac{{dx}}{\mathrm{2}{cos}^{\mathrm{2}} {x}+\sqrt{\mathrm{3}}\:{sin}^{\mathrm{2}} {x}}\:\:{i}\:{can}\:{not}\:{post}\:{by}\:+\:\:{so}\:{in}\:{comment} \\ $$

Commented by mindispower last updated on 25/Oct/20

=2∫_0 ^π (dx/(2cos^2 (x)+(√3)sin^2 (x))) =2∫_0 ^(π/2) (dx/(2cos^2 (x)+(√3)sin^2 (x)))+2∫_0 ^(π/2) (dx/(2sin^2 (x)+(√3)cos^2 (x))) ∫_0 ^(π/2) (dx/(asin^2 (x)+bcos^2 (x))),a,b>0 =∫_0 ^(π/2) (1/(bcos^2 (x)))(dx/((1+((√(a/b))tg(x))^2 )) =(1/( (√(ab))))∫_0 ^(π/2) ((d(((√a)/( (√b)))tg(x)))/(1+(((√a)/( (√b)))tg(x))^2 )) =(1/( (√(ab))))[tan^(−1) ((√(a/b))tg(x))]_0 ^(π/2) =(π/(2(√(ab)))) we find 2.(π/(2(√(2(√3)))))+((2.π)/(2(√((√3).2))))=((2π)/( (√(2(√3)))))

$$=\mathrm{2}\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\mathrm{2}{cos}^{\mathrm{2}} \left({x}\right)+\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} \left({x}\right)} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{2}{cos}^{\mathrm{2}} \left({x}\right)+\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} \left({x}\right)}+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{2}{sin}^{\mathrm{2}} \left({x}\right)+\sqrt{\mathrm{3}}{cos}^{\mathrm{2}} \left({x}\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{{asin}^{\mathrm{2}} \left({x}\right)+{bcos}^{\mathrm{2}} \left({x}\right)},{a},{b}>\mathrm{0} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{{bcos}^{\mathrm{2}} \left({x}\right)}\frac{{dx}}{\left(\mathrm{1}+\left(\sqrt{\frac{{a}}{{b}}}{tg}\left({x}\right)\right)^{\mathrm{2}} \right.} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{ab}}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{d}\left(\frac{\sqrt{{a}}}{\:\sqrt{{b}}}{tg}\left({x}\right)\right)}{\mathrm{1}+\left(\frac{\sqrt{{a}}}{\:\sqrt{{b}}}{tg}\left({x}\right)\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{{ab}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\frac{{a}}{{b}}}{tg}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\pi}{\mathrm{2}\sqrt{{ab}}} \\ $$$${we}\:{find} \\ $$$$\mathrm{2}.\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}+\frac{\mathrm{2}.\pi}{\mathrm{2}\sqrt{\sqrt{\mathrm{3}}.\mathrm{2}}}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}} \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

thank you sir

$${thank}\:{you}\:{sir} \\ $$

Commented by mindispower last updated on 25/Oct/20

withe pleasur sir i hop you doing well i dont know why but im thinking that is lectur withe residus Theorem ?

$${withe}\:{pleasur}\:{sir}\:{i}\:{hop}\:{you}\:{doing}\:{well}\:{i}\:{dont}\:{know}\:{why}\:{but} \\ $$$${im}\:{thinking}\:{that}\:{is}\:{lectur}\:{withe}\:\:{residus}\:{Theorem}\:? \\ $$

Commented by TANMAY PANACEA last updated on 25/Oct/20

i have shared this question ...other question seem similar in type

$${i}\:{have}\:{shared}\:{this}\:{question}\:...{other}\:{question}\: \\ $$$${seem}\:{similar}\:{in}\:{type} \\ $$

Commented by Tinku Tara last updated on 26/Oct/20

If you want to always start in forum by default. Change setting and enable start i Q&A forum and save forum preferences

$$\mathrm{If}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{always}\:\mathrm{start}\:\mathrm{in}\:\mathrm{forum} \\ $$$$\mathrm{by}\:\mathrm{default}.\:\mathrm{Change}\:\mathrm{setting}\:\mathrm{and} \\ $$$$\mathrm{enable}\:\mathrm{start}\:\mathrm{i}\:\mathrm{Q\&A}\:\mathrm{forum}\:\mathrm{and}\:\mathrm{save} \\ $$$$\mathrm{forum}\:\mathrm{preferences} \\ $$

Commented by Bird last updated on 25/Oct/20

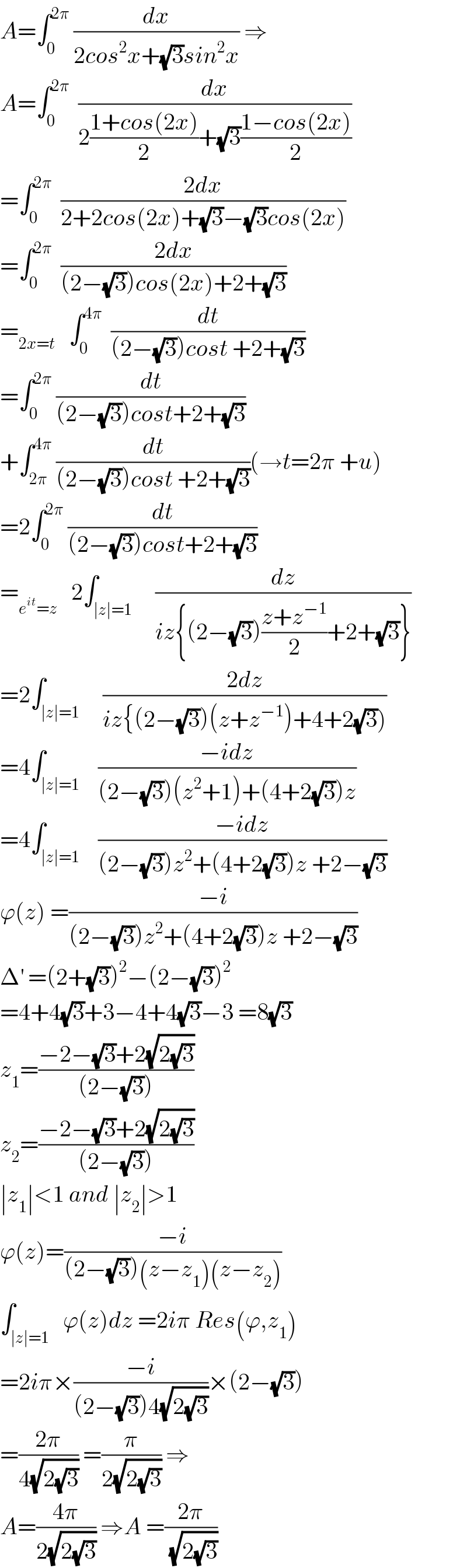
A=∫_0 ^(2π) (dx/(2cos^2 x+(√3)sin^2 x)) ⇒ A=∫_0 ^(2π) (dx/(2((1+cos(2x))/2)+(√3)((1−cos(2x))/2))) =∫_0 ^(2π) ((2dx)/(2+2cos(2x)+(√3)−(√3)cos(2x))) =∫_0 ^(2π) ((2dx)/((2−(√3))cos(2x)+2+(√3))) =_(2x=t) ∫_0 ^(4π) (dt/((2−(√3))cost +2+(√3))) =∫_0 ^(2π) (dt/((2−(√3))cost+2+(√3))) +∫_(2π) ^(4π) (dt/((2−(√3))cost +2+(√3)))(→t=2π +u) =2∫_0 ^(2π) (dt/((2−(√3))cost+2+(√3))) =_(e^(it) =z) 2∫_(∣z∣=1) (dz/(iz{(2−(√3))((z+z^(−1) )/2)+2+(√3)})) =2∫_(∣z∣=1) ((2dz)/(iz{(2−(√3))(z+z^(−1) )+4+2(√3)))) =4∫_(∣z∣=1) ((−idz)/((2−(√3))(z^2 +1)+(4+2(√3))z)) =4∫_(∣z∣=1) ((−idz)/((2−(√3))z^2 +(4+2(√3))z +2−(√3))) ϕ(z) =((−i)/((2−(√3))z^2 +(4+2(√3))z +2−(√3))) Δ^′ =(2+(√3))^2 −(2−(√3))^2 =4+4(√3)+3−4+4(√3)−3 =8(√3) z_1 =((−2−(√3)+2(√(2(√3))))/((2−(√3)))) z_2 =((−2−(√3)+2(√(2(√3))))/((2−(√3)))) ∣z_1 ∣<1 and ∣z_2 ∣>1 ϕ(z)=((−i)/((2−(√3))(z−z_1 )(z−z_2 ))) ∫_(∣z∣=1) ϕ(z)dz =2iπ Res(ϕ,z_1 ) =2iπ×((−i)/((2−(√3))4(√(2(√3)))))×(2−(√3)) =((2π)/(4(√(2(√3))))) =(π/(2(√(2(√3))))) ⇒ A=((4π)/(2(√(2(√3))))) ⇒A =((2π)/( (√(2(√3)))))

$${A}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dx}}{\mathrm{2}{cos}^{\mathrm{2}} {x}+\sqrt{\mathrm{3}}{sin}^{\mathrm{2}} {x}}\:\Rightarrow \\ $$$${A}=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dx}}{\mathrm{2}\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}+\sqrt{\mathrm{3}}\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{2}{dx}}{\mathrm{2}+\mathrm{2}{cos}\left(\mathrm{2}{x}\right)+\sqrt{\mathrm{3}}−\sqrt{\mathrm{3}}{cos}\left(\mathrm{2}{x}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{\mathrm{2}{dx}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){cos}\left(\mathrm{2}{x}\right)+\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$=_{\mathrm{2}{x}={t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\:\frac{{dt}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){cost}\:+\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dt}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){cost}+\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$+\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\frac{{dt}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){cost}\:+\mathrm{2}+\sqrt{\mathrm{3}}}\left(\rightarrow{t}=\mathrm{2}\pi\:+{u}\right) \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{{dt}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){cost}+\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$=_{{e}^{{it}} ={z}} \:\:\:\mathrm{2}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{{dz}}{{iz}\left\{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\frac{{z}+{z}^{−\mathrm{1}} }{\mathrm{2}}+\mathrm{2}+\sqrt{\mathrm{3}}\right\}} \\ $$$$=\mathrm{2}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\:\frac{\mathrm{2}{dz}}{{iz}\left\{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({z}+{z}^{−\mathrm{1}} \right)+\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right)} \\ $$$$=\mathrm{4}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−{idz}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({z}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right){z}} \\ $$$$=\mathrm{4}\int_{\mid{z}\mid=\mathrm{1}} \:\:\:\frac{−{idz}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){z}^{\mathrm{2}} +\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right){z}\:+\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\varphi\left({z}\right)\:=\frac{−{i}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right){z}^{\mathrm{2}} +\left(\mathrm{4}+\mathrm{2}\sqrt{\mathrm{3}}\right){z}\:+\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\Delta^{'} \:=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{4}+\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{3}−\mathrm{4}+\mathrm{4}\sqrt{\mathrm{3}}−\mathrm{3}\:=\mathrm{8}\sqrt{\mathrm{3}} \\ $$$${z}_{\mathrm{1}} =\frac{−\mathrm{2}−\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)} \\ $$$${z}_{\mathrm{2}} =\frac{−\mathrm{2}−\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)} \\ $$$$\mid{z}_{\mathrm{1}} \mid<\mathrm{1}\:{and}\:\mid{z}_{\mathrm{2}} \mid>\mathrm{1}\:\: \\ $$$$\varphi\left({z}\right)=\frac{−{i}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\left({z}−{z}_{\mathrm{1}} \right)\left({z}−{z}_{\mathrm{2}} \right)} \\ $$$$\int_{\mid{z}\mid=\mathrm{1}} \:\:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\:{Res}\left(\varphi,{z}_{\mathrm{1}} \right) \\ $$$$=\mathrm{2}{i}\pi×\frac{−{i}}{\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{4}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}×\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{2}\pi}{\mathrm{4}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}\:\Rightarrow \\ $$$${A}=\frac{\mathrm{4}\pi}{\mathrm{2}\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}}\:\Rightarrow{A}\:=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{2}\sqrt{\mathrm{3}}}} \\ $$

Commented by MJS_new last updated on 26/Oct/20

seems you are in editor mode go into menue (“≡”−symbol on left top) directly after starting the app and then choose forum

$$\mathrm{seems}\:\mathrm{you}\:\mathrm{are}\:\mathrm{in}\:\mathrm{editor}\:\mathrm{mode} \\ $$$$\mathrm{go}\:\mathrm{into}\:\mathrm{menue}\:\left(``\equiv''−\mathrm{symbol}\:\mathrm{on}\:\mathrm{left}\:\mathrm{top}\right) \\ $$$$\mathrm{directly}\:\mathrm{after}\:\mathrm{starting}\:\mathrm{the}\:\mathrm{app}\:\mathrm{and}\:\mathrm{then} \\ $$$$\mathrm{choose}\:{forum} \\ $$

Commented by TANMAY PANACEA last updated on 26/Oct/20

ok sir

$${ok}\:{sir} \\ $$

Commented by Tinku Tara last updated on 26/Oct/20

Answered by benjo_mathlover last updated on 25/Oct/20

using polynomial division we find that x^4 +x^3 −4x^2 +x+5=x(x^3 +x^2 −9x−9)+(5x^2 +10x+5) next we have to divide x^3 +x^2 −9x−9 by 5x^2 +10x+5 we find that x^3 +x^2 −9x−9=(5x^2 +10x+5)(((x−1)/5))+(−8x−8) Finally we divide 5x^2 +10x+5 by −8x−8 and we find that 5x^2 +10x+5=(−8x−8)[ −(5/( 8))(x+1) ] Thus gcd (x^4 +x^3 −4x^2 +x+5 , x^3 +x^2 −9x−9) = x+1

$${using}\:{polynomial}\:{division}\:{we}\:{find}\:{that}\: \\ $$$${x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +{x}+\mathrm{5}={x}\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{9}\right)+\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{5}\right) \\ $$$${next}\:{we}\:{have}\:{to}\:{divide}\:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{9}\:{by}\:\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{5} \\ $$$${we}\:{find}\:{that}\:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{9}=\left(\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{5}\right)\left(\frac{{x}−\mathrm{1}}{\mathrm{5}}\right)+\left(−\mathrm{8}{x}−\mathrm{8}\right) \\ $$$${Finally}\:{we}\:{divide}\:\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{5}\:{by}\:−\mathrm{8}{x}−\mathrm{8}\:{and}\:{we}\:{find}\:{that} \\ $$$$\mathrm{5}{x}^{\mathrm{2}} +\mathrm{10}{x}+\mathrm{5}=\left(−\mathrm{8}{x}−\mathrm{8}\right)\left[\:−\frac{\mathrm{5}}{\:\mathrm{8}}\left({x}+\mathrm{1}\right)\:\right] \\ $$$${Thus}\:{gcd}\:\left({x}^{\mathrm{4}} +{x}^{\mathrm{3}} −\mathrm{4}{x}^{\mathrm{2}} +{x}+\mathrm{5}\:,\:{x}^{\mathrm{3}} +{x}^{\mathrm{2}} −\mathrm{9}{x}−\mathrm{9}\right)\:=\:{x}+\mathrm{1} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com