
Question and Answers Forum
Question Number 119657 by bemath last updated on 26/Oct/20

Commented by som(math1967) last updated on 26/Oct/20
![I think a−b=1 is a perfect square If a,b both odd then a−b=even ∴((ab)/(a−b))∉Z [but c∈Z] if one of a,b even and other is odd ((ab)/(a−b))∈Z only a−b=1 [G.C.D of a,b,c is 1] so a−b perfect square.](Q119670.png)
Commented by bemath last updated on 26/Oct/20

Answered by 1549442205PVT last updated on 26/Oct/20
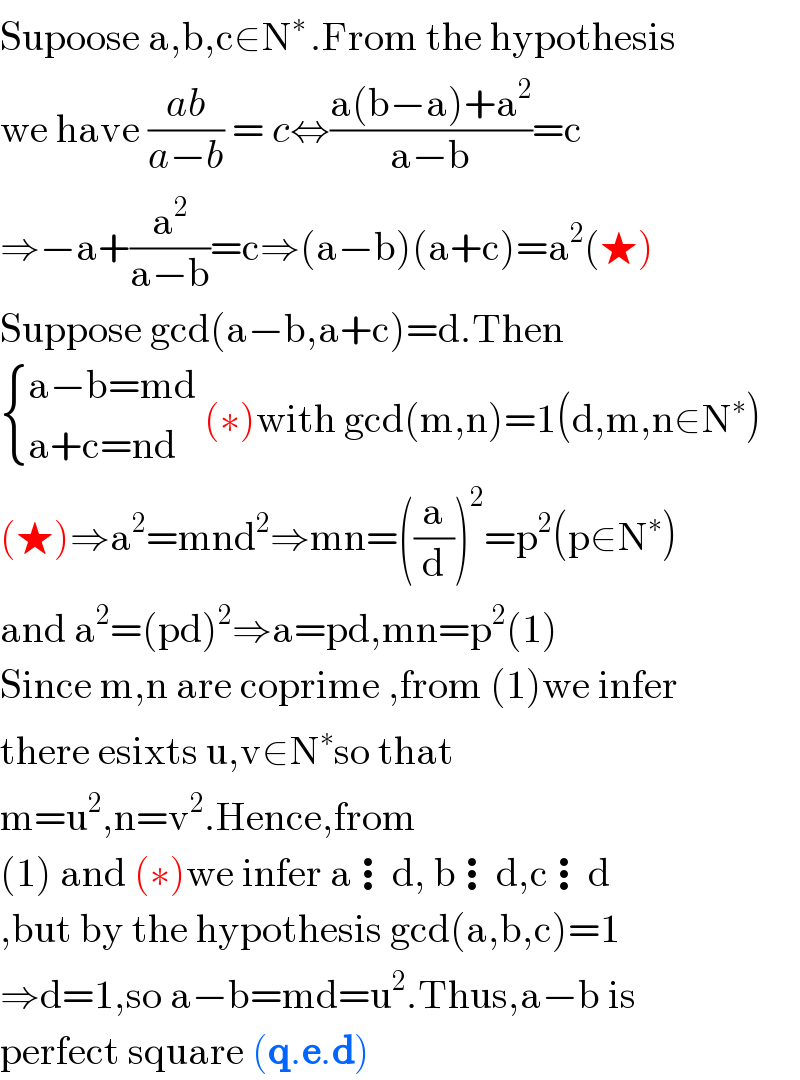
| ||
Question and Answers Forum | ||
Question Number 119657 by bemath last updated on 26/Oct/20 | ||
 | ||
Commented by som(math1967) last updated on 26/Oct/20 | ||
![I think a−b=1 is a perfect square If a,b both odd then a−b=even ∴((ab)/(a−b))∉Z [but c∈Z] if one of a,b even and other is odd ((ab)/(a−b))∈Z only a−b=1 [G.C.D of a,b,c is 1] so a−b perfect square.](Q119670.png) | ||
Commented by bemath last updated on 26/Oct/20 | ||
 | ||
Answered by 1549442205PVT last updated on 26/Oct/20 | ||
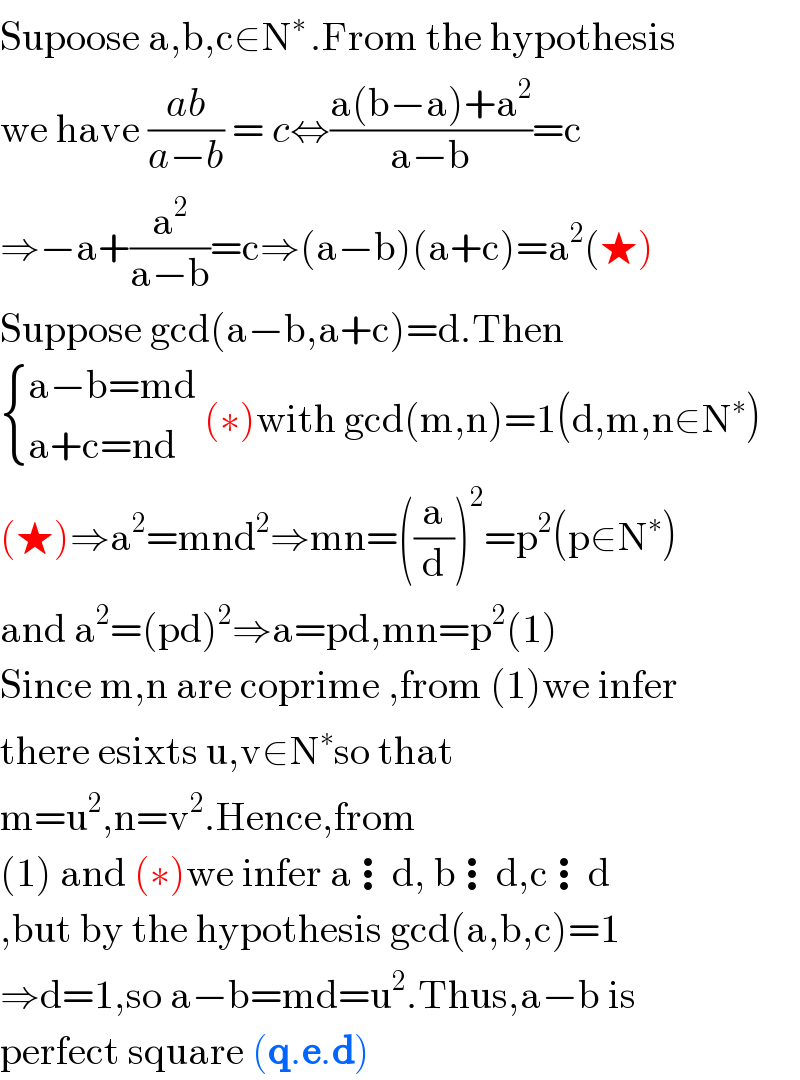 | ||
| ||