Question Number 119762 by mathmax by abdo last updated on 26/Oct/20
$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{x}^{\mathrm{4}} \mathrm{dx}}{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{8}} } \\ $$
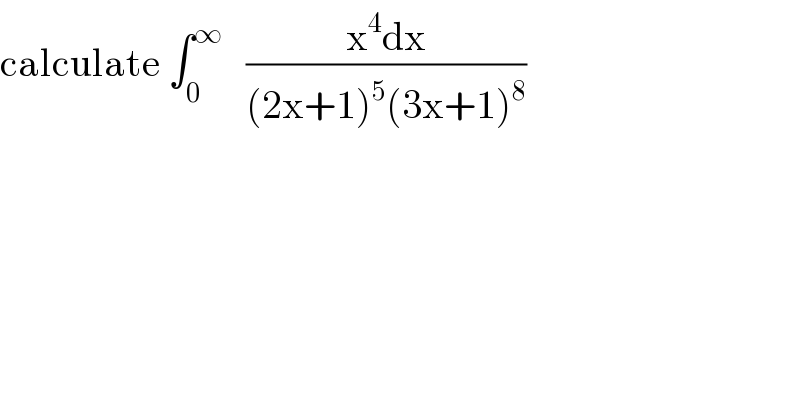
Answered by Olaf last updated on 26/Oct/20
$$\frac{\mathrm{5319686}}{\mathrm{105}}+\mathrm{124952ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$ \\ $$$$...\:\mathrm{The}\:\mathrm{calculous}\:\mathrm{is}\:\mathrm{very}\:\mathrm{long}\:! \\ $$$$\mathrm{R}\left({x}\right)\:=\:\frac{{x}^{\mathrm{4}} }{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{8}} } \\ $$$$\mathrm{R}\left({x}\right)\:=\:\frac{\mathrm{16}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{5}} }+\frac{\mathrm{320}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{3744}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$+\frac{\mathrm{37344}}{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{249904}}{\mathrm{2}{x}+\mathrm{1}}+\frac{\mathrm{3}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{8}} } \\ $$$$−\frac{\mathrm{42}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{7}} }+\frac{\mathrm{318}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{6}} }−\frac{\mathrm{1752}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} } \\ $$$$+\frac{\mathrm{7923}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{4}} }−\frac{\mathrm{31326}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{112404}}{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{374856}}{\mathrm{3}{x}+\mathrm{1}} \\ $$$$... \\ $$
Commented by mathmax by abdo last updated on 26/Oct/20
$$\mathrm{thanks}\:\mathrm{sir} \\ $$
Answered by MJS_new last updated on 26/Oct/20
![method (1) decomposition method (2) Ostrogradski both are long... method (3) ∫(x^4 /((2x+1)^5 (3x+1)^8 ))dx= [t=((2x+1)/(3x+1)) → dx=−(3x+1)^2 dt] =−∫(((t−1)^4 (3t−2)^7 )/t^5 )dt this seems easier to me... (((t−1)^4 (3t−2)^7 )/t^5 )= =2187t^6 −18954t^5 +74358t^4 −174312t^3 + +271323t^2 −294462t−((124952)/t)+((47888)/t^2 )− −((12192)/t^3 )+((1856)/t^4 )−((128)/t^5 )+227388 and these are easy to integrate](Q119766.png)
$$\mathrm{method}\:\left(\mathrm{1}\right)\:\mathrm{decomposition} \\ $$$$\mathrm{method}\:\left(\mathrm{2}\right)\:\mathrm{Ostrogradski} \\ $$$$\mathrm{both}\:\mathrm{are}\:\mathrm{long}... \\ $$$$\mathrm{method}\:\left(\mathrm{3}\right) \\ $$$$\int\frac{{x}^{\mathrm{4}} }{\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{8}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{2}{x}+\mathrm{1}}{\mathrm{3}{x}+\mathrm{1}}\:\rightarrow\:{dx}=−\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{2}} {dt}\right] \\ $$$$=−\int\frac{\left({t}−\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{3}{t}−\mathrm{2}\right)^{\mathrm{7}} }{{t}^{\mathrm{5}} }{dt} \\ $$$$\mathrm{this}\:\mathrm{seems}\:\mathrm{easier}\:\mathrm{to}\:\mathrm{me}... \\ $$$$\frac{\left({t}−\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{3}{t}−\mathrm{2}\right)^{\mathrm{7}} }{{t}^{\mathrm{5}} }= \\ $$$$=\mathrm{2187}{t}^{\mathrm{6}} −\mathrm{18954}{t}^{\mathrm{5}} +\mathrm{74358}{t}^{\mathrm{4}} −\mathrm{174312}{t}^{\mathrm{3}} + \\ $$$$\:\:\:\:\:+\mathrm{271323}{t}^{\mathrm{2}} −\mathrm{294462}{t}−\frac{\mathrm{124952}}{{t}}+\frac{\mathrm{47888}}{{t}^{\mathrm{2}} }− \\ $$$$\:\:\:\:\:−\frac{\mathrm{12192}}{{t}^{\mathrm{3}} }+\frac{\mathrm{1856}}{{t}^{\mathrm{4}} }−\frac{\mathrm{128}}{{t}^{\mathrm{5}} }+\mathrm{227388} \\ $$$$\mathrm{and}\:\mathrm{these}\:\mathrm{are}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{integrate} \\ $$
Commented by mathmax by abdo last updated on 27/Oct/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\:\mathrm{mjs} \\ $$
Commented by MJS_new last updated on 27/Oct/20
$$\mathrm{as}\:\mathrm{always},\:\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
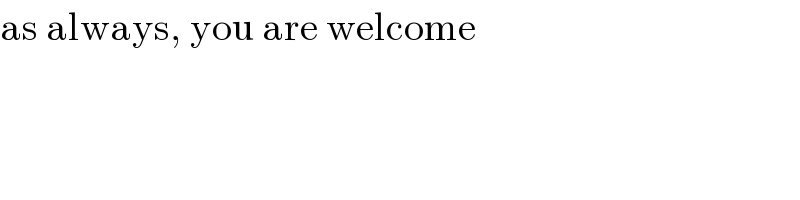
Answered by mathmax by abdo last updated on 27/Oct/20
![let I =∫_0 ^∞ (x^4 /((2x+1)^5 (3x+1)^8 ))dx ⇒ I =∫_0 ^∞ (x^4 /((((2x+1)/(3x+1)))^5 (3x+1)^(13) ))dx we do the chang.((2x+1)/(3x+1)) =t ⇒ 2x+1 =3tx+t ⇒(2−3t)x=t−1 ⇒x =((t−1)/(2−3t)) ⇒ (dx/dt)=((2−3t−(t−1)(−3))/((2−3t)^2 ))=((2−3t+3t−3)/((2−3t)^2 ))=((−1)/((2−3t)^2 )) 3x+1 =((3t−3)/(2−3t))+1 =((3t−3+2−3t)/(2−3t))=((−1)/(2−3t)) ⇒ I =∫_1 ^(2/3) (((t−1)^4 )/((2−3t)^4 ))×(1/(t^5 (((−1)/(2−3t)))^(13) ))×((−1)/((2−3t)^2 ))dt =∫_(2/3) ^1 (((t−1)^4 )/((2−3t)^6 t^5 ))×(3t−2)^(13) dt =∫_(2/3) ^1 (((t−1)^4 (3t−2)^7 )/t^5 )dt we have (t−1)^4 =Σ_(k=0) ^4 C_4 ^k t^k (−1)^k =1−C_4 ^1 t +C_4 ^2 t^2 −C_4 ^3 t^3 +t^4 =1−4t+6t^2 −4t^3 +t^4 ⇒ I =∫_(2/3) ^1 ((1/t^5 )−(4/t^4 )+(6/t^3 )−(4/t^2 ) +(1/t))(3t−2)^7 dt =∫_(2/3) ^1 (((3t−2)^7 )/t^5 )dt−4∫_(2/3) ^1 (((3t−2)^7 )/t^4 ) +6∫_(2/3) ^1 (((3t−2)^7 )/t^3 )dt−4∫_(2/3) ^1 (((3t−2)^7 )/t^2 ) +∫_(2/3) ^1 (((3t−2)^7 )/t)dt those integrals can be calculsted by binome formula ∫_(2/3) ^1 (((3t−2)^7 )/t^5 )dt =∫_(2/3) ^1 ((Σ_(k=0) ^7 C_7 ^k (3t)^k (−2)^(7−k) )/t^5 )dt =∫_(2/3) ^1 Σ_(k=0) ^7 C_7 ^k 3^k (−2)^(7−k) t^(k−5) dt =Σ_(k=0 and k≠4) ^7 C_7 ^k 3^k (−2)^(7−k) [(1/(k−4))t^(k−4) ]_(2/3) ^1 +C_7 ^4 3^4 (−2)^3 [ln∣t∣]_(2/3) ^1 =Σ_(k=0 and k≠4) ^7 ((C_7 ^k 3^k (−2)^(7−k) )/(k−4))(1−((2/3))^(k−4) )−C_7 ^4 3^4 (−2)^3 ln((2/3)) ....](Q119783.png)
$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{4}} }{\left(\mathrm{2x}+\mathrm{1}\right)^{\mathrm{5}} \left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{8}} }\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{4}} }{\left(\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{3x}+\mathrm{1}}\right)^{\mathrm{5}} \left(\mathrm{3x}+\mathrm{1}\right)^{\mathrm{13}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{chang}.\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{3x}+\mathrm{1}}\:=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{2x}+\mathrm{1}\:=\mathrm{3tx}+\mathrm{t}\:\Rightarrow\left(\mathrm{2}−\mathrm{3t}\right)\mathrm{x}=\mathrm{t}−\mathrm{1}\:\Rightarrow\mathrm{x}\:=\frac{\mathrm{t}−\mathrm{1}}{\mathrm{2}−\mathrm{3t}}\:\Rightarrow \\ $$$$\frac{\mathrm{dx}}{\mathrm{dt}}=\frac{\mathrm{2}−\mathrm{3t}−\left(\mathrm{t}−\mathrm{1}\right)\left(−\mathrm{3}\right)}{\left(\mathrm{2}−\mathrm{3t}\right)^{\mathrm{2}} }=\frac{\mathrm{2}−\mathrm{3t}+\mathrm{3t}−\mathrm{3}}{\left(\mathrm{2}−\mathrm{3t}\right)^{\mathrm{2}} }=\frac{−\mathrm{1}}{\left(\mathrm{2}−\mathrm{3t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{3x}+\mathrm{1}\:=\frac{\mathrm{3t}−\mathrm{3}}{\mathrm{2}−\mathrm{3t}}+\mathrm{1}\:=\frac{\mathrm{3t}−\mathrm{3}+\mathrm{2}−\mathrm{3t}}{\mathrm{2}−\mathrm{3t}}=\frac{−\mathrm{1}}{\mathrm{2}−\mathrm{3t}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{1}} ^{\frac{\mathrm{2}}{\mathrm{3}}} \:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} }{\left(\mathrm{2}−\mathrm{3t}\right)^{\mathrm{4}} }×\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{5}} \left(\frac{−\mathrm{1}}{\mathrm{2}−\mathrm{3t}}\right)^{\mathrm{13}} }×\frac{−\mathrm{1}}{\left(\mathrm{2}−\mathrm{3t}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\:\:\:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} }{\left(\mathrm{2}−\mathrm{3t}\right)^{\mathrm{6}} \mathrm{t}^{\mathrm{5}} }×\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{13}} \:\mathrm{dt} \\ $$$$=\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\:\frac{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{5}} }\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{4}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{4}} \:\mathrm{C}_{\mathrm{4}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{k}} =\mathrm{1}−\mathrm{C}_{\mathrm{4}} ^{\mathrm{1}} \mathrm{t}\:+\mathrm{C}_{\mathrm{4}} ^{\mathrm{2}} \mathrm{t}^{\mathrm{2}} −\mathrm{C}_{\mathrm{4}} ^{\mathrm{3}} \mathrm{t}^{\mathrm{3}} \:+\mathrm{t}^{\mathrm{4}} \\ $$$$=\mathrm{1}−\mathrm{4t}+\mathrm{6t}^{\mathrm{2}} −\mathrm{4t}^{\mathrm{3}} +\mathrm{t}^{\mathrm{4}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{5}} }−\frac{\mathrm{4}}{\mathrm{t}^{\mathrm{4}} }+\frac{\mathrm{6}}{\mathrm{t}^{\mathrm{3}} }−\frac{\mathrm{4}}{\mathrm{t}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{t}}\right)\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} \mathrm{dt} \\ $$$$=\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{5}} }\mathrm{dt}−\mathrm{4}\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \frac{\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{4}} }\:+\mathrm{6}\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{3}} }\mathrm{dt}−\mathrm{4}\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{2}} } \\ $$$$+\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}}\mathrm{dt}\:\:\mathrm{those}\:\mathrm{integrals}\:\mathrm{can}\:\mathrm{be}\:\mathrm{calculsted}\:\mathrm{by}\:\mathrm{binome}\:\mathrm{formula} \\ $$$$\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\frac{\left(\mathrm{3t}−\mathrm{2}\right)^{\mathrm{7}} }{\mathrm{t}^{\mathrm{5}} }\mathrm{dt}\:=\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \left(\mathrm{3t}\right)^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{7}−\mathrm{k}} }{\mathrm{t}^{\mathrm{5}} }\mathrm{dt} \\ $$$$=\int_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{7}} \mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \mathrm{3}^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{7}−\mathrm{k}} \mathrm{t}^{\mathrm{k}−\mathrm{5}} \mathrm{dt} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{4}} ^{\mathrm{7}} \:\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \:\mathrm{3}^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{7}−\mathrm{k}} \:\:\left[\frac{\mathrm{1}}{\mathrm{k}−\mathrm{4}}\mathrm{t}^{\mathrm{k}−\mathrm{4}} \right]_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \:\:+\mathrm{C}_{\mathrm{7}} ^{\mathrm{4}} \:\mathrm{3}^{\mathrm{4}} \left(−\mathrm{2}\right)^{\mathrm{3}} \left[\mathrm{ln}\mid\mathrm{t}\mid\right]_{\frac{\mathrm{2}}{\mathrm{3}}} ^{\mathrm{1}} \\ $$$$=\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{and}\:\mathrm{k}\neq\mathrm{4}} ^{\mathrm{7}} \:\frac{\mathrm{C}_{\mathrm{7}} ^{\mathrm{k}} \:\mathrm{3}^{\mathrm{k}} \left(−\mathrm{2}\right)^{\mathrm{7}−\mathrm{k}} }{\mathrm{k}−\mathrm{4}}\left(\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{k}−\mathrm{4}} \right)−\mathrm{C}_{\mathrm{7}} ^{\mathrm{4}} \:\mathrm{3}^{\mathrm{4}} \left(−\mathrm{2}\right)^{\mathrm{3}} \mathrm{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$.... \\ $$$$ \\ $$