
Question and Answers Forum
Question Number 119807 by Ar Brandon last updated on 27/Oct/20
![Let f be a real-valued function defined on the inte- rval [−1, 1]. If the area of the equilateral triangle with (0, 0) and (x, f(x)) as two vertices is (√3)/4, then f(x) is equal to (A) (√(1−x^2 )) (B) (√(1+x^2 )) (C) −(√(1−x^2 )) (D) −(√(1+x^2 ))](Q119807.png)
Answered by TANMAY PANACEA last updated on 28/Oct/20
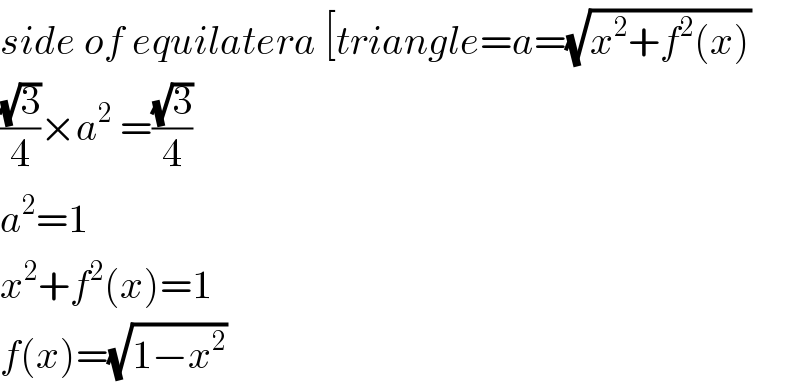
Commented by Ar Brandon last updated on 28/Oct/20
Thank you Sir
Commented by Ar Brandon last updated on 28/Oct/20
Thanks Sir
Commented by Ar Brandon last updated on 03/Nov/20
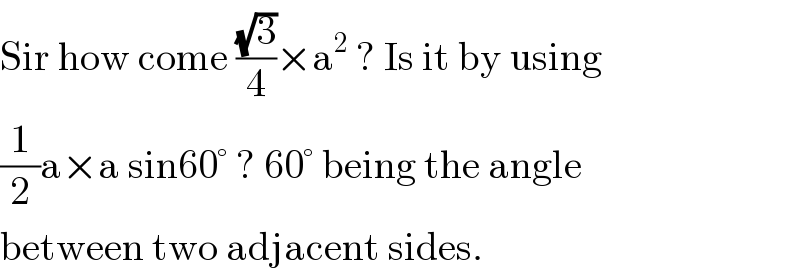
Commented by TANMAY PANACEA last updated on 28/Oct/20
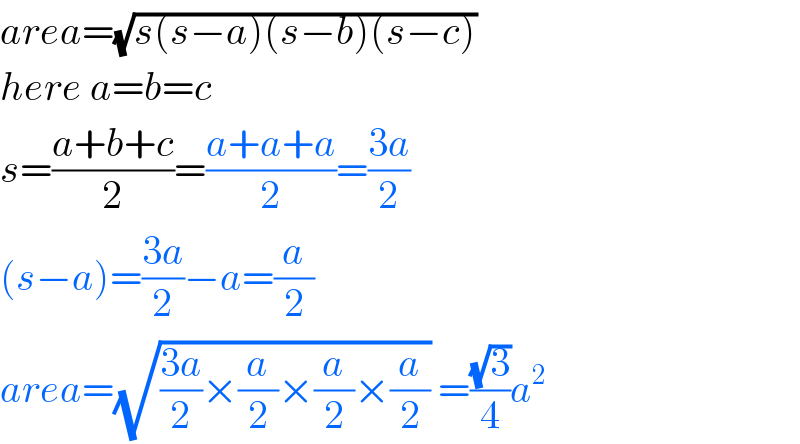
Commented by TANMAY PANACEA last updated on 28/Oct/20
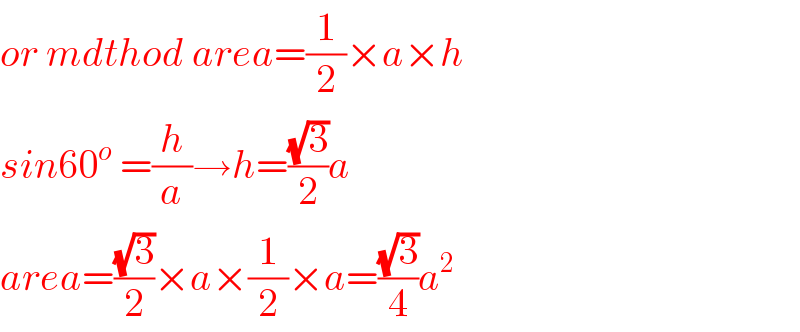
Commented by TANMAY PANACEA last updated on 28/Oct/20

