
Question and Answers Forum
Question Number 119821 by bemath last updated on 27/Oct/20
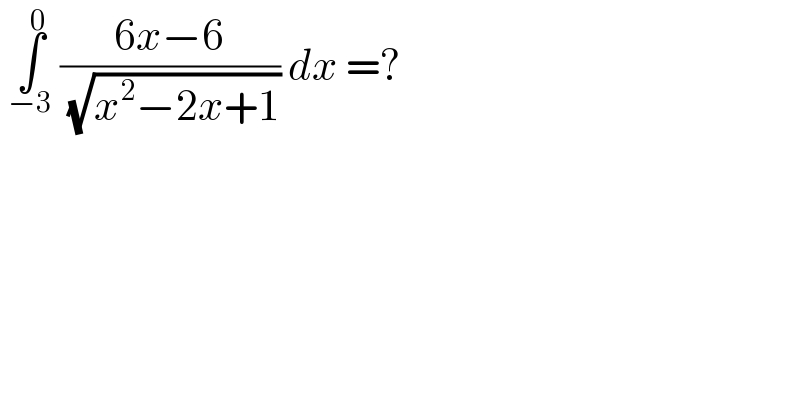
Answered by bobhans last updated on 27/Oct/20
![∫_(−3) ^0 ((6(x−1))/( (√((x−1)^2 )))) dx =∫_(−3) ^0 ((6(x−1))/(∣x−1∣)) dx = −6∫_(−3) ^0 dx = −6(x)] _(−3)^0 = −6(0+3)=−18](Q119826.png)
Answered by Olaf last updated on 27/Oct/20
![x^2 −2x+1 is defined for x∈[−3;0] I = ∫_(−3) ^0 ((6(x−1))/( (√((x^2 −1)^2 ))))dx I = ∫_(−3) ^0 ((6(x−1))/( ∣x−1∣))dx I = ∫_(−3) ^0 ((6(x−1))/( 1−x))dx = −6(0+3) = −18](Q119828.png)
Answered by 1549442205PVT last updated on 27/Oct/20
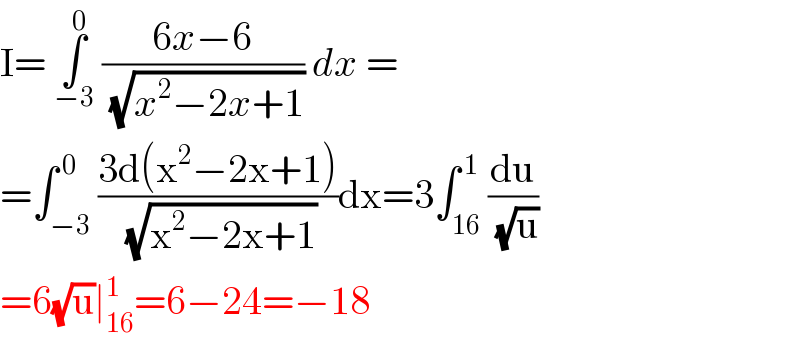
| ||
Question and Answers Forum | ||
Question Number 119821 by bemath last updated on 27/Oct/20 | ||
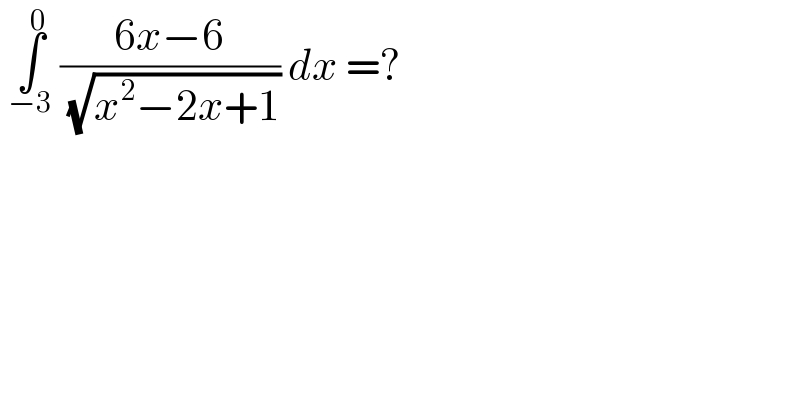 | ||
Answered by bobhans last updated on 27/Oct/20 | ||
![∫_(−3) ^0 ((6(x−1))/( (√((x−1)^2 )))) dx =∫_(−3) ^0 ((6(x−1))/(∣x−1∣)) dx = −6∫_(−3) ^0 dx = −6(x)] _(−3)^0 = −6(0+3)=−18](Q119826.png) | ||
| ||
Answered by Olaf last updated on 27/Oct/20 | ||
![x^2 −2x+1 is defined for x∈[−3;0] I = ∫_(−3) ^0 ((6(x−1))/( (√((x^2 −1)^2 ))))dx I = ∫_(−3) ^0 ((6(x−1))/( ∣x−1∣))dx I = ∫_(−3) ^0 ((6(x−1))/( 1−x))dx = −6(0+3) = −18](Q119828.png) | ||
| ||
Answered by 1549442205PVT last updated on 27/Oct/20 | ||
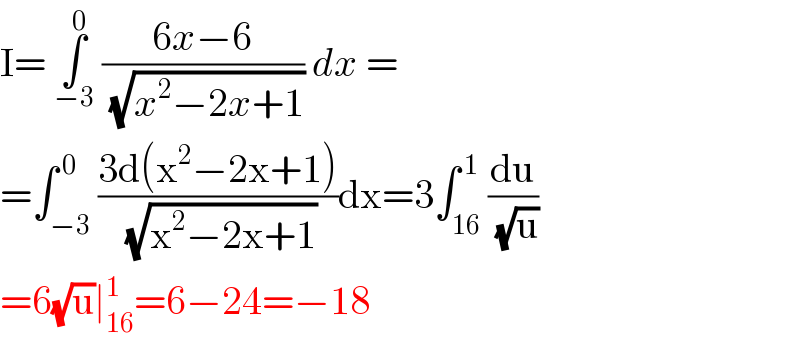 | ||
| ||