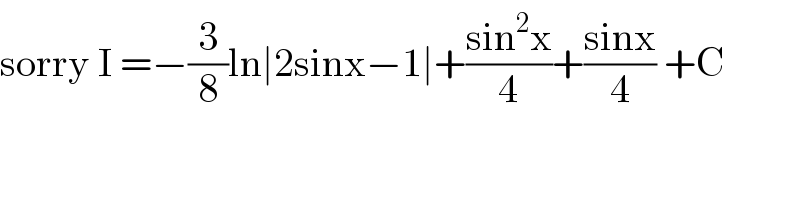Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 119939 by huotpat last updated on 28/Oct/20

Answered by bramlexs22 last updated on 28/Oct/20

∫ (((1−sin^2 x) cos x dx )/(1−2sin x)) [ let sin x = s ] ∫ (((1−s^2 )ds)/(1−2s)) = ∫ ((s^2 −1)/(2s−1)) ds = ∫ ((1/2)s+(1/4))ds−(3/4)∫ (ds/(2s−1)) = (1/4)s^2 +(1/4)s−(3/8)ln ∣2s−1∣ + c = (1/4)sin x(sin x+1)−(3/8)ln ∣2sin x−1∣ + c

∫(1−sin2x)cosxdx1−2sinx[letsinx=s]∫(1−s2)ds1−2s=∫s2−12s−1ds=∫(12s+14)ds−34∫ds2s−1=14s2+14s−38ln∣2s−1∣+c=14sinx(sinx+1)−38ln∣2sinx−1∣+c

Answered by Dwaipayan Shikari last updated on 28/Oct/20

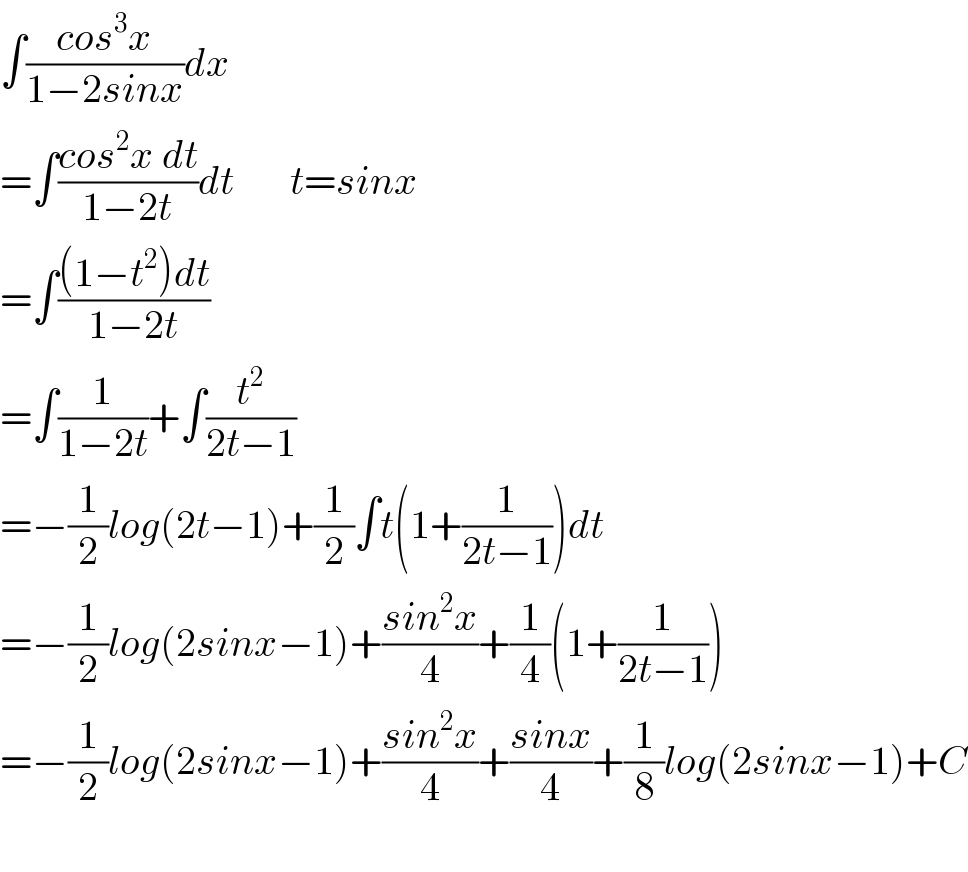
∫((cos^3 x)/(1−2sinx))dx =∫((cos^2 x dt)/(1−2t))dt t=sinx =∫(((1−t^2 )dt)/(1−2t)) =∫(1/(1−2t))+∫(t^2 /(2t−1)) =−(1/2)log(2t−1)+(1/2)∫t(1+(1/(2t−1)))dt =−(1/2)log(2sinx−1)+((sin^2 x)/4)+(1/4)(1+(1/(2t−1))) =−(1/2)log(2sinx−1)+((sin^2 x)/4)+((sinx)/4)+(1/8)log(2sinx−1)+C

∫cos3x1−2sinxdx=∫cos2xdt1−2tdtt=sinx=∫(1−t2)dt1−2t=∫11−2t+∫t22t−1=−12log(2t−1)+12∫t(1+12t−1)dt=−12log(2sinx−1)+sin2x4+14(1+12t−1)=−12log(2sinx−1)+sin2x4+sinx4+18log(2sinx−1)+C

Answered by mathmax by abdo last updated on 28/Oct/20

I=∫ ((cos^3 x)/(1−2sinx))dx ⇒I=∫ ((cosx(1−sin^2 x))/(1−2sinx))dx =∫ ((cosx)/(1−2sinx))dx−∫ ((cosx sin^2 x)/(1−2sinx))dx =U−V U=∫ ((cosx)/(1−2sinx))dx =−(1/2)ln∣1−2sinx∣ +c_1 V=∫((sin^2 x cosxdx)/(1−2sinx)) =_(sinx=t) ∫ ((t^2 dt)/(1−2t)) =−∫ (t^2 /(2t−1))dt =−(1/4)∫ ((4t^2 −1+1)/(2t−1))dt=−(1/4)∫(((2t−1)(2t+1)+1)/(2t−1))dt =−(1/4)∫(2t+1)dt−(1/4)∫(dt/(2t−1))=−(t^2 /4)−(t/4)−(1/8)ln∣2t−1∣ +c_2 =−((sin^2 x)/4)−((sinx)/4)−(1/8)ln∣2sinx−1∣+c_2 ⇒ I =−(1/2)ln∣2sinx−1∣+(1/8)ln∣2sinx−1∣+((sin^2 x)/4) +((sinx)/4) +C I=−(3/8)ln∣2sinx−1∣+(1/8)ln∣2sinx−1∣+((sin^2 x)/4)+((sinx)/4) +C

I=∫cos3x1−2sinxdx⇒I=∫cosx(1−sin2x)1−2sinxdx=∫cosx1−2sinxdx−∫cosxsin2x1−2sinxdx=U−VU=∫cosx1−2sinxdx=−12ln∣1−2sinx∣+c1V=∫sin2xcosxdx1−2sinx=sinx=t∫t2dt1−2t=−∫t22t−1dt=−14∫4t2−1+12t−1dt=−14∫(2t−1)(2t+1)+12t−1dt=−14∫(2t+1)dt−14∫dt2t−1=−t24−t4−18ln∣2t−1∣+c2=−sin2x4−sinx4−18ln∣2sinx−1∣+c2⇒I=−12ln∣2sinx−1∣+18ln∣2sinx−1∣+sin2x4+sinx4+CI=−38ln∣2sinx−1∣+18ln∣2sinx−1∣+sin2x4+sinx4+C

Commented by mathmax by abdo last updated on 28/Oct/20

sorry I =−(3/8)ln∣2sinx−1∣+((sin^2 x)/4)+((sinx)/4) +C

sorryI=−38ln∣2sinx−1∣+sin2x4+sinx4+C

Terms of Service

Privacy Policy

Contact: info@tinkutara.com