Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 119956 by bobhans last updated on 28/Oct/20

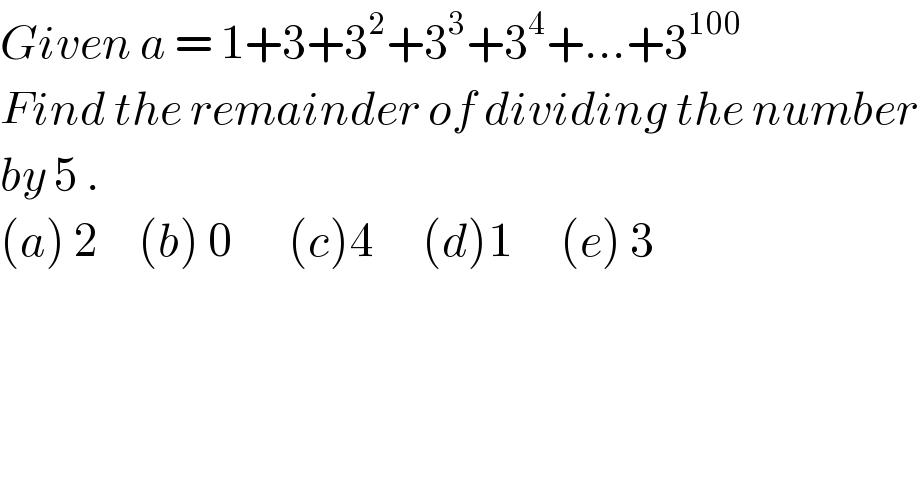
Given a = 1+3+3^2 +3^3 +3^4 +...+3^(100) Find the remainder of dividing the number by 5 . (a) 2 (b) 0 (c)4 (d)1 (e) 3

$${Given}\:{a}\:=\:\mathrm{1}+\mathrm{3}+\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +\mathrm{3}^{\mathrm{4}} +...+\mathrm{3}^{\mathrm{100}} \\ $$$${Find}\:{the}\:{remainder}\:{of}\:{dividing}\:{the}\:{number} \\ $$$${by}\:\mathrm{5}\:. \\ $$$$\left({a}\right)\:\mathrm{2}\:\:\:\:\:\left({b}\right)\:\mathrm{0}\:\:\:\:\:\:\:\left({c}\right)\mathrm{4}\:\:\:\:\:\:\left({d}\right)\mathrm{1}\:\:\:\:\:\:\left({e}\right)\:\mathrm{3} \\ $$

Answered by talminator2856791 last updated on 08/Sep/21

a = Σ_(k = 0) ^(24) 3^(4k) (1+3^2 ) + Σ_(k = 0) ^(24) 3^(4k+1) (1+3^2 ) + 3^(100) Σ_(k = 0) ^(24) 3^(4k) (1+3^2 ) = 10Σ_(k = 0) ^(24) 3^(4k) Σ_(k = 0) ^(24) 3^(4k) (1+3^2 ) = 10Σ_(k = 0) ^(24) 3^(4k+1) → 5 ∣10Σ_(k = 0) ^(24) 3^(4k) , 5∣10Σ_(k = 0) ^(24) 3^(4k+1) → 5∣1+3+3^2 +.....+3^(99) ⇒ 5∣3(1+3+3^2 +.....+3^(99) ) = 5∣3+3^2 +3^3 +.....+3^(100) ⇒ 1+3+3^2 +......+3^(100) ≡ 1 (mod 5) answer: d

$$\:{a}\:=\:\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}} \left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)\:+\:\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\mathrm{3}^{\mathrm{4}{k}+\mathrm{1}} \left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)\:+\:\mathrm{3}^{\mathrm{100}} \: \\ $$$$\:\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}} \left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)\:=\:\mathrm{10}\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}} \\ $$$$\:\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}} \left(\mathrm{1}+\mathrm{3}^{\mathrm{2}} \right)\:=\:\mathrm{10}\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}+\mathrm{1}} \\ $$$$\:\rightarrow\:\mathrm{5}\:\mid\mathrm{10}\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}} \:,\:\:\:\mathrm{5}\mid\mathrm{10}\underset{{k}\:=\:\mathrm{0}} {\overset{\mathrm{24}} {\sum}}\:\mathrm{3}^{\mathrm{4}{k}+\mathrm{1}} \\ $$$$\:\rightarrow\:\mathrm{5}\mid\mathrm{1}+\mathrm{3}+\mathrm{3}^{\mathrm{2}} +.....+\mathrm{3}^{\mathrm{99}} \\ $$$$\: \\ $$$$\:\Rightarrow\:\mathrm{5}\mid\mathrm{3}\left(\mathrm{1}+\mathrm{3}+\mathrm{3}^{\mathrm{2}} +.....+\mathrm{3}^{\mathrm{99}} \right) \\ $$$$\:=\:\:\mathrm{5}\mid\mathrm{3}+\mathrm{3}^{\mathrm{2}} +\mathrm{3}^{\mathrm{3}} +.....+\mathrm{3}^{\mathrm{100}} \\ $$$$\: \\ $$$$\:\Rightarrow\:\mathrm{1}+\mathrm{3}+\mathrm{3}^{\mathrm{2}} +......+\mathrm{3}^{\mathrm{100}} \:\equiv\:\mathrm{1}\:\left(\mathrm{mod}\:\mathrm{5}\right) \\ $$$$\:\mathrm{answer}:\:{d} \\ $$

Answered by TANMAY PANACEA last updated on 28/Oct/20

S=((3^(101) −1)/(3−1))=(1/2)(3^(101) −1) 3^1 =3 3^2 =9 3^3 =27 3^4 =81 3^5 =243 3^6 =729 so last digit repets (3→9→7→1) ((101)/4)→25 cycle of(3→9→7→1)+plus 1 last digit of 3^(101) is 3 (now last digit 3)−1 so last digit becomes=2 when devided by 2 last digit becomes 1 ((3^(101) −1)/2)= last digit=1 ((3^(101) −1)/2)=(5×even multiple )+last digit=1

$${S}=\frac{\mathrm{3}^{\mathrm{101}} −\mathrm{1}}{\mathrm{3}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{3}^{\mathrm{101}} −\mathrm{1}\right) \\ $$$$\mathrm{3}^{\mathrm{1}} =\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{2}} =\mathrm{9} \\ $$$$\mathrm{3}^{\mathrm{3}} =\mathrm{27} \\ $$$$\mathrm{3}^{\mathrm{4}} =\mathrm{81} \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{243} \\ $$$$\mathrm{3}^{\mathrm{6}} =\mathrm{729} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{last}}\:\boldsymbol{{digit}}\:\boldsymbol{{repets}}\:\left(\mathrm{3}\rightarrow\mathrm{9}\rightarrow\mathrm{7}\rightarrow\mathrm{1}\right) \\ $$$$\frac{\mathrm{101}}{\mathrm{4}}\rightarrow\mathrm{25}\:{cycle}\:{of}\left(\mathrm{3}\rightarrow\mathrm{9}\rightarrow\mathrm{7}\rightarrow\mathrm{1}\right)+\boldsymbol{{plus}}\:\mathrm{1} \\ $$$$\boldsymbol{{last}}\:\boldsymbol{{digit}}\:\boldsymbol{{of}}\:\mathrm{3}^{\mathrm{101}} \:\boldsymbol{{is}}\:\:\mathrm{3} \\ $$$$\left(\boldsymbol{{now}}\:\boldsymbol{{last}}\:\boldsymbol{{digit}}\:\mathrm{3}\right)−\mathrm{1} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{last}}\:\boldsymbol{{digit}}\:\boldsymbol{{becomes}}=\mathrm{2} \\ $$$$\boldsymbol{{when}}\:\boldsymbol{{devided}}\:\boldsymbol{{by}}\:\mathrm{2} \\ $$$$\boldsymbol{{last}}\:\boldsymbol{{digit}}\:\boldsymbol{{becomes}}\:\mathrm{1} \\ $$$$\frac{\mathrm{3}^{\mathrm{101}} −\mathrm{1}}{\mathrm{2}}=\:\:{last}\:{digit}=\mathrm{1} \\ $$$$\frac{\mathrm{3}^{\mathrm{101}} −\mathrm{1}}{\mathrm{2}}=\left(\mathrm{5}×{even}\:{multiple}\:\right)+\boldsymbol{{last}}\:\boldsymbol{{digit}}=\mathrm{1} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com