Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 119989 by mnjuly1970 last updated on 28/Oct/20

Answered by mathmax by abdo last updated on 28/Oct/20

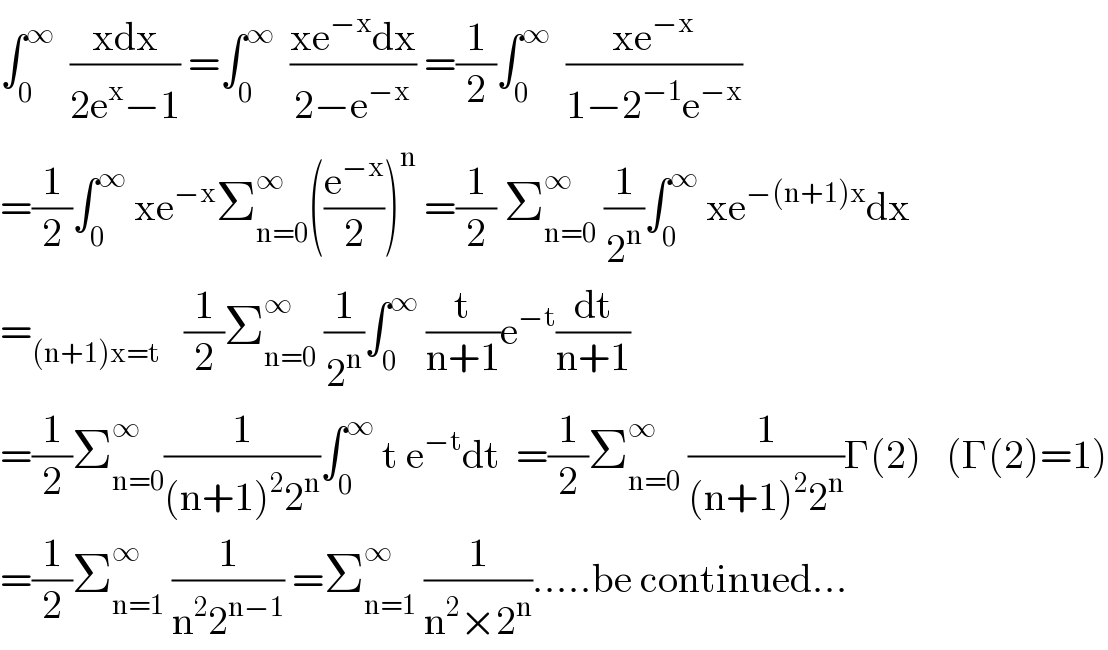
∫_0 ^∞ ((xdx)/(2e^x −1)) =∫_0 ^∞ ((xe^(−x) dx)/(2−e^(−x) )) =(1/2)∫_0 ^∞ ((xe^(−x) )/(1−2^(−1) e^(−x) )) =(1/2)∫_0 ^∞ xe^(−x) Σ_(n=0) ^∞ ((e^(−x) /2))^n =(1/2) Σ_(n=0) ^∞ (1/2^n )∫_0 ^∞ xe^(−(n+1)x) dx =_((n+1)x=t) (1/2)Σ_(n=0) ^∞ (1/2^n )∫_0 ^∞ (t/(n+1))e^(−t) (dt/(n+1)) =(1/2)Σ_(n=0) ^∞ (1/((n+1)^2 2^n ))∫_0 ^∞ t e^(−t) dt =(1/2)Σ_(n=0) ^∞ (1/((n+1)^2 2^n ))Γ(2) (Γ(2)=1) =(1/2)Σ_(n=1) ^∞ (1/(n^2 2^(n−1) )) =Σ_(n=1) ^∞ (1/(n^2 ×2^n )).....be continued...

$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{xdx}}{\mathrm{2e}^{\mathrm{x}} −\mathrm{1}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{xe}^{−\mathrm{x}} \mathrm{dx}}{\mathrm{2}−\mathrm{e}^{−\mathrm{x}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{xe}^{−\mathrm{x}} }{\mathrm{1}−\mathrm{2}^{−\mathrm{1}} \mathrm{e}^{−\mathrm{x}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{xe}^{−\mathrm{x}} \sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(\frac{\mathrm{e}^{−\mathrm{x}} }{\mathrm{2}}\right)^{\mathrm{n}} \:=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{xe}^{−\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}} \mathrm{dx} \\ $$$$=_{\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}=\mathrm{t}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{n}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}}{\mathrm{n}+\mathrm{1}}\mathrm{e}^{−\mathrm{t}} \frac{\mathrm{dt}}{\mathrm{n}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{2}^{\mathrm{n}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}\:\mathrm{e}^{−\mathrm{t}} \mathrm{dt}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \mathrm{2}^{\mathrm{n}} }\Gamma\left(\mathrm{2}\right)\:\:\:\left(\Gamma\left(\mathrm{2}\right)=\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} \mathrm{2}^{\mathrm{n}−\mathrm{1}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{n}} }.....\mathrm{be}\:\mathrm{continued}... \\ $$

Commented by mnjuly1970 last updated on 29/Oct/20

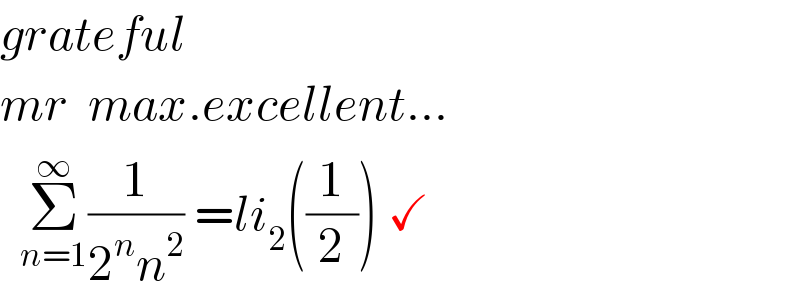
grateful mr max.excellent... Σ_(n=1) ^∞ (1/(2^n n^2 )) =li_2 ((1/2)) ✓

$${grateful} \\ $$$${mr}\:\:{max}.{excellent}... \\ $$$$\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{n}} {n}^{\mathrm{2}} }\:={li}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\checkmark \\ $$

Commented by Bird last updated on 29/Oct/20

you are welcome

$${you}\:{are}\:{welcome} \\ $$

Answered by mindispower last updated on 30/Oct/20

∫_0 ^∞ ((ln^2 (x)ln(x+1))/(x(x+1)))dx =∫_0 ^1 ((ln^2 (x)ln(1+x))/(x(x+1)))+∫_1 ^∞ ((ln^2 (x)ln(1+x))/(x(x+1)))dx_(x→(1/x)) =∫_0 ^1 ((ln^2 (x)ln(1+x)(x+1−x))/(x(x+1)))dx+∫_0 ^1 ((ln^2 (x)ln(1+(1/x)))/(1+x))dx =∫_0 ^1 ((ln^2 (x)ln(1+x))/x)dx−∫_0 ^1 ((ln^2 (x)ln(1+x))/(1+x))dx +∫_0 ^1 ((ln^2 (x)ln(1+x))/(1+x))dx−∫_0 ^1 ((ln^3 (x))/(1+x))dx =∫_0 ^1 ((ln^2 (x)ln(1+x)dx)/x)−∫_0 ^1 ((ln^3 (x))/(1+x)) =[((ln^3 (x)ln(1+x))/3)]_0 ^1 −∫_0 ^1 ((ln^3 (x))/(3(1+x)))dx−∫_0 ^1 ((ln^3 (x))/(1+x))dx =(4/3)∫_0 ^1 (((−ln(x))^3 )/(1+x))dx_(x=e^(−t) ) =(4/3)∫_0 ^∞ (t^3 /(1+e^(−t) ))e^(−t) dt=(4/3)Σ_(k≥0) ∫_0 ^∞ t^3 e^(−(1+k)t) dt =(4/3)Σ_(k≥0) ∫_0 ^∞ (−1)^k ((t^3 e^(−t) dt)/((1+k)^4 )) =(4/3)Σ_(k≥0) (((−1)^k )/((1+k)^4 ))Γ(4)=8Σ_(k≥0) (((−1)^k )/((1+k)^4 )) 8(Σ_(k≥0) (1/((2k+1)^4 ))−Σ_(k≥0) (1/((2k+2)^4 )))=8(ζ(4)−(1/(16))ζ(4)−((ζ(4))/(16))) =8.((14)/(16))ζ(4)=7ζ(5)

$$\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left({x}+\mathrm{1}\right)}{{x}\left({x}+\mathrm{1}\right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}\left({x}+\mathrm{1}\right)}+\int_{\mathrm{1}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}\left({x}+\mathrm{1}\right)}{dx}_{{x}\rightarrow\frac{\mathrm{1}}{{x}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)\left({x}+\mathrm{1}−{x}\right)}{{x}\left({x}+\mathrm{1}\right)}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right){dx}}{{x}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{1}+{x}} \\ $$$$=\left[\frac{{ln}^{\mathrm{3}} \left({x}\right){ln}\left(\mathrm{1}+{x}\right)}{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{3}\left(\mathrm{1}+{x}\right)}{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{3}} \left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(−{ln}\left({x}\right)\right)^{\mathrm{3}} }{\mathrm{1}+{x}}{dx}_{{x}={e}^{−{t}} } \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{3}} }{\mathrm{1}+{e}^{−{t}} }{e}^{−{t}} {dt}=\frac{\mathrm{4}}{\mathrm{3}}\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{3}} {e}^{−\left(\mathrm{1}+{k}\right){t}} {dt} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\underset{{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{k}} \frac{{t}^{\mathrm{3}} {e}^{−{t}} {dt}}{\left(\mathrm{1}+{k}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{1}+{k}\right)^{\mathrm{4}} }\Gamma\left(\mathrm{4}\right)=\mathrm{8}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{1}+{k}\right)^{\mathrm{4}} } \\ $$$$\mathrm{8}\left(\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{4}} }−\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{2}\right)^{\mathrm{4}} }\right)=\mathrm{8}\left(\zeta\left(\mathrm{4}\right)−\frac{\mathrm{1}}{\mathrm{16}}\zeta\left(\mathrm{4}\right)−\frac{\zeta\left(\mathrm{4}\right)}{\mathrm{16}}\right) \\ $$$$=\mathrm{8}.\frac{\mathrm{14}}{\mathrm{16}}\zeta\left(\mathrm{4}\right)=\mathrm{7}\zeta\left(\mathrm{5}\right) \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 30/Oct/20

bravo mr mindspower very nice as always.. thank you...

$${bravo}\:{mr}\:{mindspower}\: \\ $$$$\:{very}\:{nice}\:{as}\:{always}.. \\ $$$${thank}\:{you}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com