Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 120211 by bemath last updated on 30/Oct/20

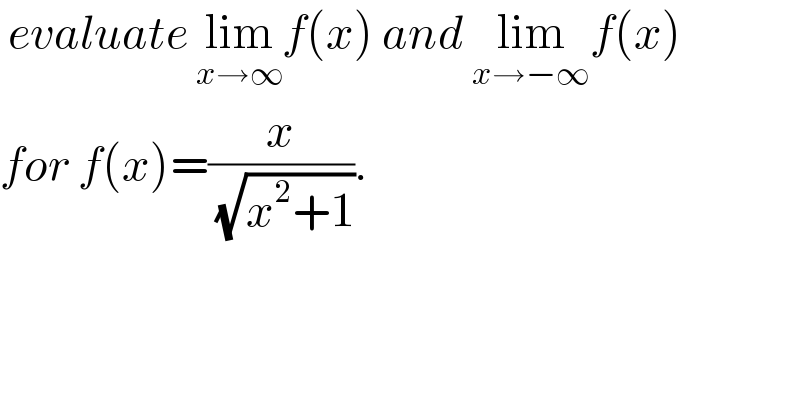
evaluate lim_(x→∞) f(x) and lim_(x→−∞) f(x) for f(x)=(x/( (√(x^2 +1)))).

$$\:{evaluate}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)\:{and}\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left({x}\right) \\ $$$${for}\:{f}\left({x}\right)=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}. \\ $$

Answered by Ar Brandon last updated on 30/Oct/20

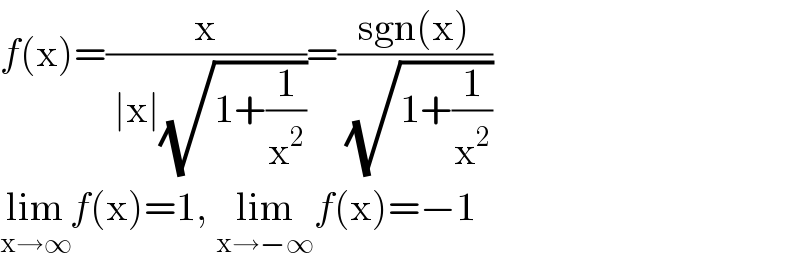
f(x)=(x/( ∣x∣(√(1+(1/x^2 )))))=((sgn(x))/( (√(1+(1/x^2 ))))) lim_(x→∞) f(x)=1, lim_(x→−∞) f(x)=−1

$${f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\:\mid\mathrm{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}=\frac{\mathrm{sgn}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}} \\ $$$$\underset{\mathrm{x}\rightarrow\infty} {\mathrm{lim}}{f}\left(\mathrm{x}\right)=\mathrm{1},\:\underset{\mathrm{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left(\mathrm{x}\right)=−\mathrm{1} \\ $$

Commented by Dwaipayan Shikari last updated on 30/Oct/20

বাংলা শিখছো?

Commented by Ar Brandon last updated on 30/Oct/20

না, আমি কিছু মজা করছি������

Answered by benjo_mathlover last updated on 30/Oct/20

Rewrite the expression for f(x) as follows : f(x)=(x/( (√(x^2 (1+(1/x^2 )))))) f(x) = (x/( (√x^2 ) (√(1+(1/x^2 ))))) =(x/(∣x∣(√(1+(1/x^2 ))))) f(x)= ((sgn x)/( (√(1+(1/x^2 ))))) ; [ where sgn x = (x/(∣x∣))= { ((1, if x>0)),((−1, if x<0)) :} The factor (√(1+(1/x^2 ))) approaches 1 as x→∞ or −∞ therefore { ((lim_(x→∞) f(x)=1)),((lim_(x→−∞) f(x)=−1)) :}

$${Rewrite}\:{the}\:{expression}\:{for} \\ $$$${f}\left({x}\right)\:{as}\:{follows}\::\:{f}\left({x}\right)=\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}} \\ $$$${f}\left({x}\right)\:=\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} }\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\:=\frac{{x}}{\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}} \\ $$$${f}\left({x}\right)=\:\frac{{sgn}\:{x}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}}\:;\:\left[\:{where}\:{sgn}\:{x}\:=\:\frac{{x}}{\mid{x}\mid}=\begin{cases}{\mathrm{1},\:{if}\:{x}>\mathrm{0}}\\{−\mathrm{1},\:{if}\:{x}<\mathrm{0}}\end{cases}\right. \\ $$$${The}\:{factor}\:\sqrt{\mathrm{1}+\left(\mathrm{1}/{x}^{\mathrm{2}} \right)}\:{approaches}\:\mathrm{1}\:{as}\:{x}\rightarrow\infty\:{or}\:−\infty \\ $$$${therefore}\:\begin{cases}{\underset{{x}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{1}}\\{\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left({x}\right)=−\mathrm{1}}\end{cases} \\ $$

Answered by mathmax by abdo last updated on 30/Oct/20

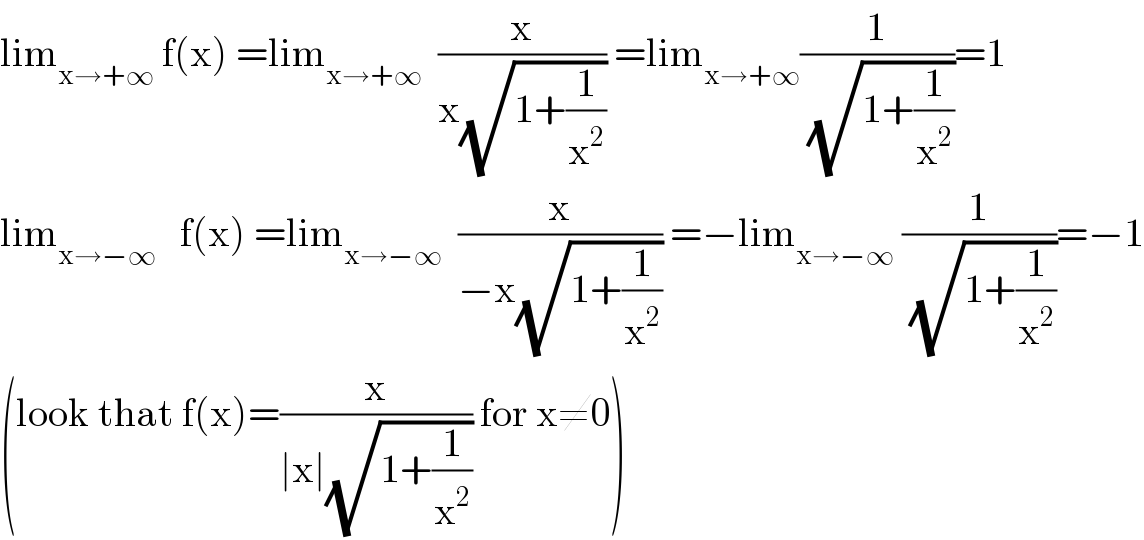
lim_(x→+∞) f(x) =lim_(x→+∞) (x/(x(√(1+(1/x^2 ))))) =lim_(x→+∞) (1/(√(1+(1/x^2 ))))=1 lim_(x→−∞) f(x) =lim_(x→−∞) (x/(−x(√(1+(1/x^2 ))))) =−lim_(x→−∞) (1/(√(1+(1/x^2 ))))=−1 (look that f(x)=(x/(∣x∣(√(1+(1/x^2 ))))) for x≠0)

$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\frac{\mathrm{x}}{\mathrm{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \frac{\mathrm{1}}{\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}=\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \:\:\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \:\:\frac{\mathrm{x}}{−\mathrm{x}\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}\:=−\mathrm{lim}_{\mathrm{x}\rightarrow−\infty} \:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}=−\mathrm{1} \\ $$$$\left(\mathrm{look}\:\mathrm{that}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}}{\mid\mathrm{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}}\:\mathrm{for}\:\mathrm{x}\neq\mathrm{0}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com