Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 120268 by bramlexs22 last updated on 30/Oct/20

Answered by mathmax by abdo last updated on 30/Oct/20

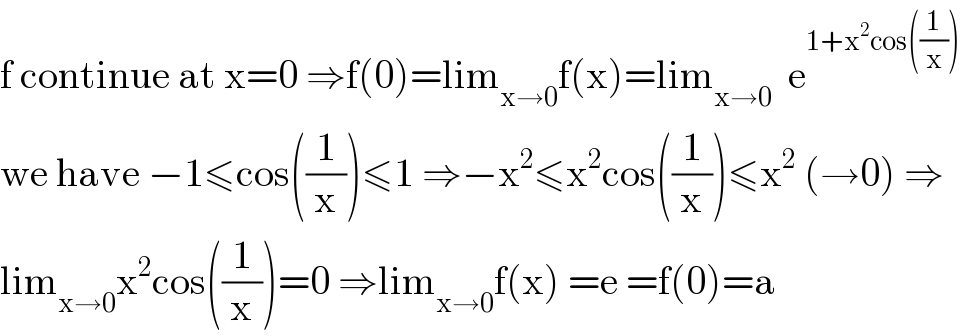
f continue at x=0 ⇒f(0)=lim_(x→0) f(x)=lim_(x→0) e^(1+x^2 cos((1/x))) we have −1≤cos((1/x))≤1 ⇒−x^2 ≤x^2 cos((1/x))≤x^2 (→0) ⇒ lim_(x→0) x^2 cos((1/x))=0 ⇒lim_(x→0) f(x) =e =f(0)=a

$$\mathrm{f}\:\mathrm{continue}\:\mathrm{at}\:\mathrm{x}=\mathrm{0}\:\Rightarrow\mathrm{f}\left(\mathrm{0}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\:\mathrm{e}^{\mathrm{1}+\mathrm{x}^{\mathrm{2}} \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:−\mathrm{1}\leqslant\mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\leqslant\mathrm{1}\:\Rightarrow−\mathrm{x}^{\mathrm{2}} \leqslant\mathrm{x}^{\mathrm{2}} \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\leqslant\mathrm{x}^{\mathrm{2}} \:\left(\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{x}^{\mathrm{2}} \mathrm{cos}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{0}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}\:=\mathrm{f}\left(\mathrm{0}\right)=\mathrm{a} \\ $$

Answered by bemath last updated on 30/Oct/20

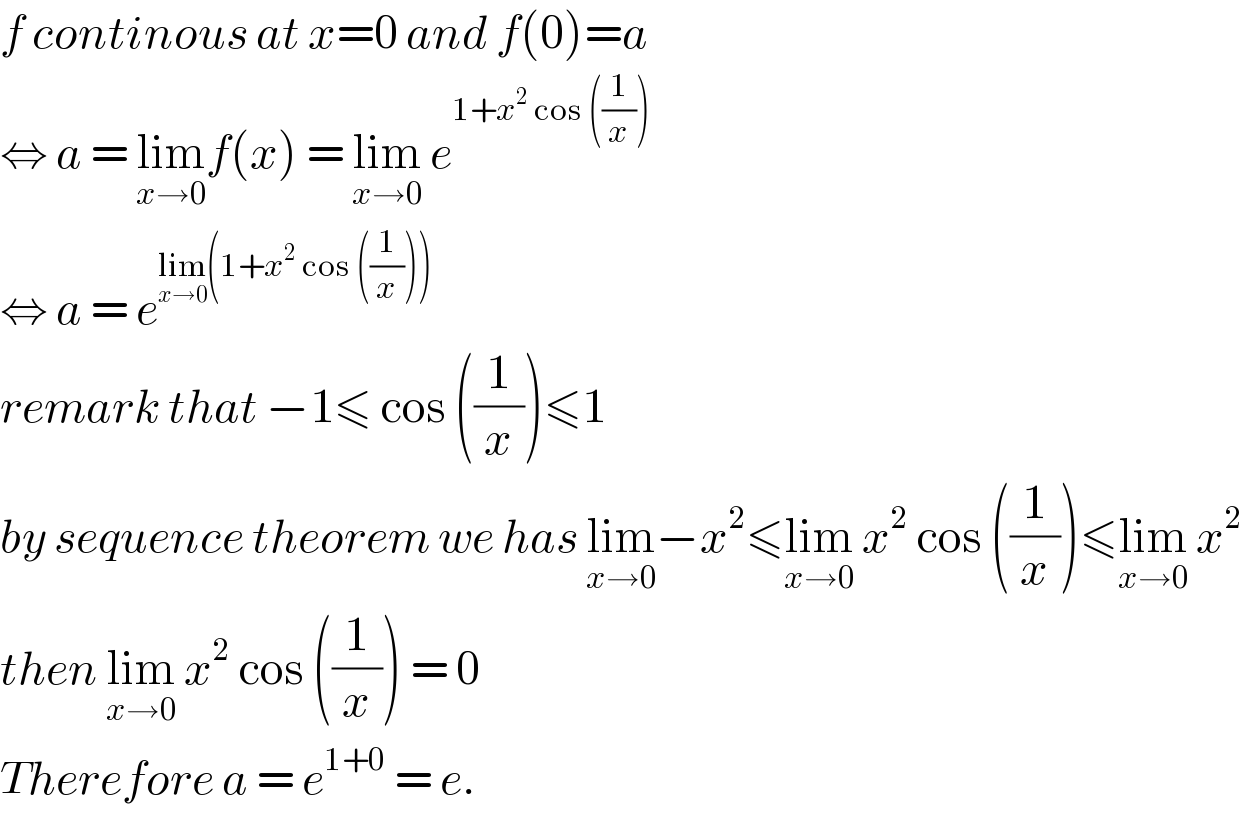
f continous at x=0 and f(0)=a ⇔ a = lim_(x→0) f(x) = lim_(x→0) e^(1+x^2 cos ((1/x))) ⇔ a = e^(lim_(x→0) (1+x^2 cos ((1/x)))) remark that −1≤ cos ((1/x))≤1 by sequence theorem we has lim_(x→0) −x^2 ≤lim_(x→0) x^2 cos ((1/x))≤lim_(x→0) x^2 then lim_(x→0) x^2 cos ((1/x)) = 0 Therefore a = e^(1+0) = e.

$${f}\:{continous}\:{at}\:{x}=\mathrm{0}\:{and}\:{f}\left(\mathrm{0}\right)={a} \\ $$$$\Leftrightarrow\:{a}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{\mathrm{1}+{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)} \\ $$$$\Leftrightarrow\:{a}\:=\:{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\right)} \\ $$$${remark}\:{that}\:−\mathrm{1}\leqslant\:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\leqslant\mathrm{1} \\ $$$${by}\:{sequence}\:{theorem}\:{we}\:{has}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−{x}^{\mathrm{2}} \leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\leqslant\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \\ $$$${then}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{\mathrm{2}} \:\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\:=\:\mathrm{0} \\ $$$${Therefore}\:{a}\:=\:{e}^{\mathrm{1}+\mathrm{0}} \:=\:{e}.\: \\ $$

Answered by TITA last updated on 30/Oct/20

if f is continious at x=0 hence lim_(x→0^− ) f(x)= lim_(x→0^+ ) f(x)=f(0) f(x)=e^(1+x^2 cos ((1/x))) x≠0 −1⪕cos ((1/x))⪕1 ⇒ −x^2 ⪕x^2 cos ((1/x))≤x^2 applying sandwich theorem ⇒lim_(x→0) x^2 cos ((1/x))=0 f(0)=e^(1+0) =e ⇒a=e

$$\mathrm{if}\:\mathrm{f}\:\mathrm{is}\:\mathrm{continious}\:\mathrm{at}\:\mathrm{x}=\mathrm{0}\:\mathrm{hence} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}f}\left(\mathrm{x}\right)=\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{0}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{e}^{\mathrm{1}+\mathrm{x}^{\mathrm{2}} \mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)} \:\:\mathrm{x}\neq\mathrm{0}\:\:\:\:\: \\ $$$$−\mathrm{1}\eqslantless\mathrm{cos}\:\left(\frac{\mathrm{1}}{{x}}\right)\eqslantless\mathrm{1}\:\Rightarrow\:−\mathrm{x}^{\mathrm{2}} \eqslantless\mathrm{x}^{\mathrm{2}} \mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\leqslant\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{applying}\:\mathrm{sandwich}\:\mathrm{theorem}\: \\ $$$$\Rightarrow\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}x}^{\mathrm{2}} \mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{0}\:\:\:\:\mathrm{f}\left(\mathrm{0}\right)=\mathrm{e}^{\mathrm{1}+\mathrm{0}} =\mathrm{e}\: \\ $$$$\Rightarrow{a}={e} \\ $$

Commented by bemath last updated on 30/Oct/20

what it sandwich theorem?

$${what}\:{it}\:{sandwich}\:{theorem}? \\ $$

Commented by mathmax by abdo last updated on 08/Nov/20

this sandwich is good....

$$\mathrm{this}\:\mathrm{sandwich}\:\mathrm{is}\:\mathrm{good}.... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com