
Question and Answers Forum
Question Number 120324 by mathocean1 last updated on 30/Oct/20
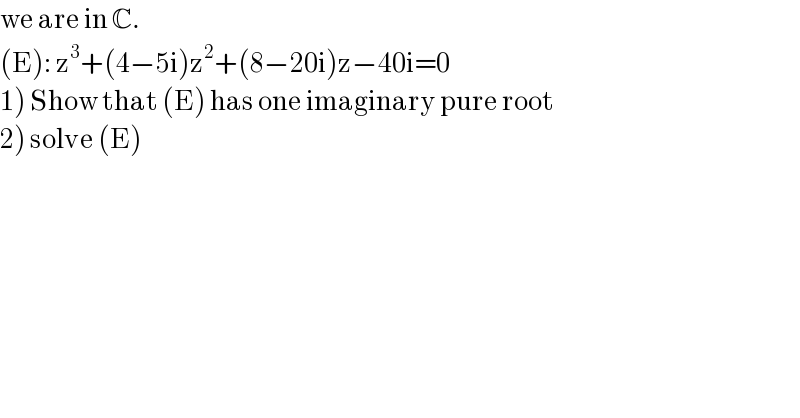
Answered by Olaf last updated on 31/Oct/20
![(1) Let z = iy z^3 +(4−5i)z^2 +(8−20i)z−40i = −iy^3 −(4−5i)y^2 +(20+8i)y−40i = −4y^2 +20y+i(−y^3 +5y^2 +8y−40) = −4y(y−5)−i(y^3 −5y^2 −8y+40) If y = 5 : −4y(y−5) = 0 and y^3 −5y^2 −8y+40 = 125−125−40+40 = 0 ⇒ 5i is a root of the polynome z^3 +(4−5i)z^2 +(8−20i)z−40i z^3 +(4−5i)z^2 +(8−20i)z−40i = (z−5i)(z^2 +wz+8) By identification : { ((w−5i = 4−5i)),((−5wi+8 = 8−20i)) :} ⇒ w = 4 z^3 +(4−5i)z^2 +(8−20i)z−40i = (z−5i)(z^2 +4z+8) = (z−5i)[(z+2)^2 +4] (z+2)^2 +4 = 0 ⇔ z = −1±i ⇒ S = {−1−i ; −1+i ; 5i }](Q120412.png)
| ||
Question and Answers Forum | ||
Question Number 120324 by mathocean1 last updated on 30/Oct/20 | ||
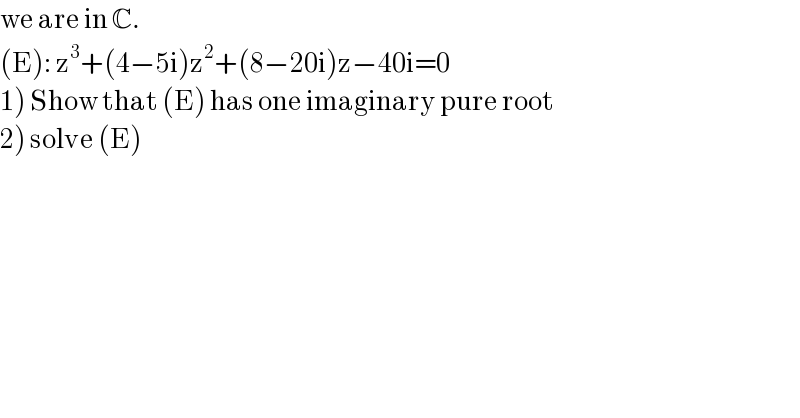 | ||
Answered by Olaf last updated on 31/Oct/20 | ||
![(1) Let z = iy z^3 +(4−5i)z^2 +(8−20i)z−40i = −iy^3 −(4−5i)y^2 +(20+8i)y−40i = −4y^2 +20y+i(−y^3 +5y^2 +8y−40) = −4y(y−5)−i(y^3 −5y^2 −8y+40) If y = 5 : −4y(y−5) = 0 and y^3 −5y^2 −8y+40 = 125−125−40+40 = 0 ⇒ 5i is a root of the polynome z^3 +(4−5i)z^2 +(8−20i)z−40i z^3 +(4−5i)z^2 +(8−20i)z−40i = (z−5i)(z^2 +wz+8) By identification : { ((w−5i = 4−5i)),((−5wi+8 = 8−20i)) :} ⇒ w = 4 z^3 +(4−5i)z^2 +(8−20i)z−40i = (z−5i)(z^2 +4z+8) = (z−5i)[(z+2)^2 +4] (z+2)^2 +4 = 0 ⇔ z = −1±i ⇒ S = {−1−i ; −1+i ; 5i }](Q120412.png) | ||
| ||