Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 12040 by Mr Chheang Chantria last updated on 10/Apr/17

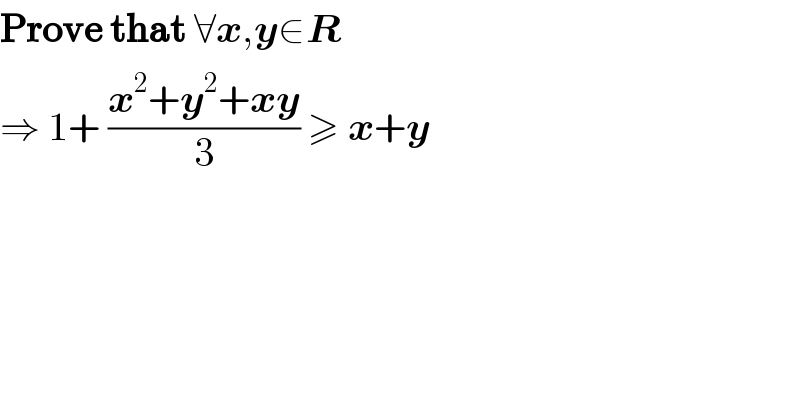
Prove that ∀x,y∈R ⇒ 1+ ((x^2 +y^2 +xy)/3) ≥ x+y

$$\boldsymbol{\mathrm{Prove}}\:\boldsymbol{\mathrm{that}}\:\forall\boldsymbol{{x}},\boldsymbol{{y}}\in\boldsymbol{{R}} \\ $$$$\Rightarrow\:\mathrm{1}+\:\frac{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{xy}}}{\mathrm{3}}\:\geqslant\:\boldsymbol{{x}}+\boldsymbol{{y}} \\ $$

Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 10/Apr/17

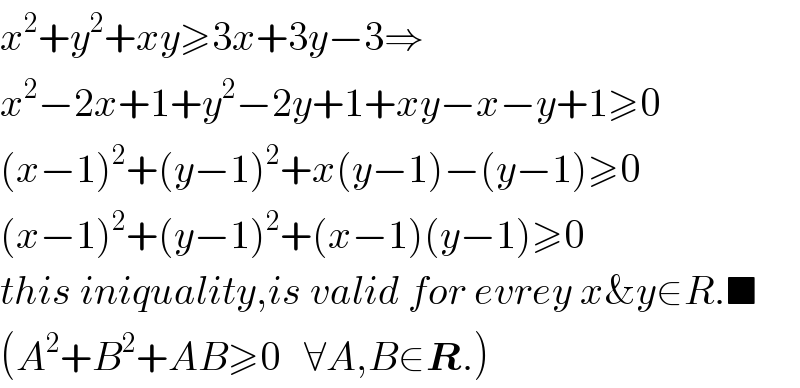
x^2 +y^2 +xy≥3x+3y−3⇒ x^2 −2x+1+y^2 −2y+1+xy−x−y+1≥0 (x−1)^2 +(y−1)^2 +x(y−1)−(y−1)≥0 (x−1)^2 +(y−1)^2 +(x−1)(y−1)≥0 this iniquality,is valid for evrey x&y∈R.■ (A^2 +B^2 +AB≥0 ∀A,B∈R.)

$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{xy}\geqslant\mathrm{3}{x}+\mathrm{3}{y}−\mathrm{3}\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}+{y}^{\mathrm{2}} −\mathrm{2}{y}+\mathrm{1}+{xy}−{x}−{y}+\mathrm{1}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} +{x}\left({y}−\mathrm{1}\right)−\left({y}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} +\left({x}−\mathrm{1}\right)\left({y}−\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$${this}\:{iniquality},{is}\:{valid}\:{for}\:{evrey}\:{x\&y}\in{R}.\blacksquare \\ $$$$\left({A}^{\mathrm{2}} +{B}^{\mathrm{2}} +{AB}\geqslant\mathrm{0}\:\:\:\forall{A},{B}\in\boldsymbol{{R}}.\right) \\ $$

Commented by Mr Chheang Chantria last updated on 11/Apr/17

Nice solution. Thanks you

$$\boldsymbol{{Nice}}\:\boldsymbol{{solution}}.\:\boldsymbol{{Thanks}}\:\boldsymbol{{you}} \\ $$

Answered by ajfour last updated on 10/Apr/17

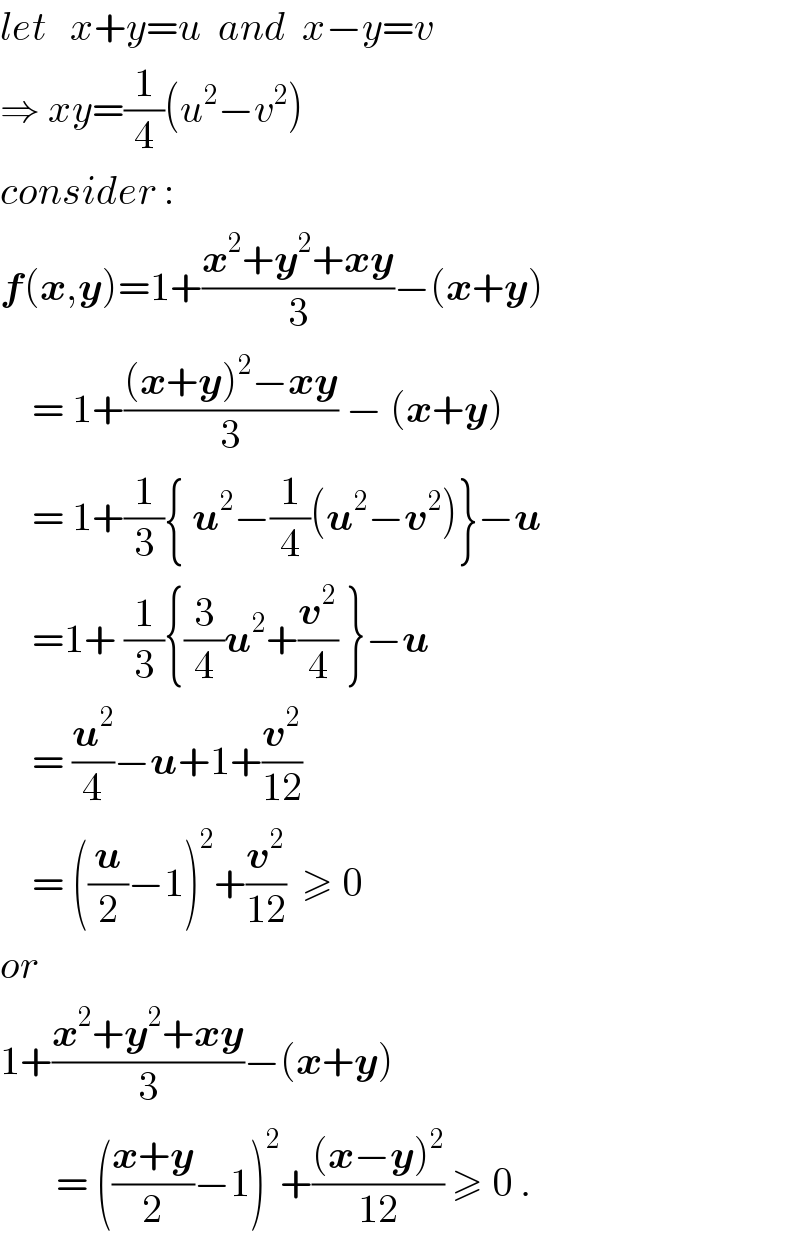
let x+y=u and x−y=v ⇒ xy=(1/4)(u^2 −v^2 ) consider : f(x,y)=1+((x^2 +y^2 +xy)/3)−(x+y) = 1+(((x+y)^2 −xy)/3) − (x+y) = 1+(1/3){ u^2 −(1/4)(u^2 −v^2 )}−u =1+ (1/3){(3/4)u^2 +(v^2 /4) }−u = (u^2 /4)−u+1+(v^2 /(12)) = ((u/2)−1)^2 +(v^2 /(12)) ≥ 0 or 1+((x^2 +y^2 +xy)/3)−(x+y) = (((x+y)/2)−1)^2 +(((x−y)^2 )/(12)) ≥ 0 .

$${let}\:\:\:{x}+{y}={u}\:\:{and}\:\:{x}−{y}={v} \\ $$$$\Rightarrow\:{xy}=\frac{\mathrm{1}}{\mathrm{4}}\left({u}^{\mathrm{2}} −{v}^{\mathrm{2}} \right) \\ $$$${consider}\:: \\ $$$$\boldsymbol{{f}}\left(\boldsymbol{{x}},\boldsymbol{{y}}\right)=\mathrm{1}+\frac{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{xy}}}{\mathrm{3}}−\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right) \\ $$$$\:\:\:\:=\:\mathrm{1}+\frac{\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right)^{\mathrm{2}} −\boldsymbol{{xy}}}{\mathrm{3}}\:−\:\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right) \\ $$$$\:\:\:\:=\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\left\{\:\boldsymbol{{u}}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{4}}\left(\boldsymbol{{u}}^{\mathrm{2}} −\boldsymbol{{v}}^{\mathrm{2}} \right)\right\}−\boldsymbol{{u}} \\ $$$$\:\:\:\:=\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{3}}{\mathrm{4}}\boldsymbol{{u}}^{\mathrm{2}} +\frac{\boldsymbol{{v}}^{\mathrm{2}} }{\mathrm{4}}\:\right\}−\boldsymbol{{u}} \\ $$$$\:\:\:\:=\:\frac{\boldsymbol{{u}}^{\mathrm{2}} }{\mathrm{4}}−\boldsymbol{{u}}+\mathrm{1}+\frac{\boldsymbol{{v}}^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\:\:\:\:=\:\left(\frac{\boldsymbol{{u}}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\boldsymbol{{v}}^{\mathrm{2}} }{\mathrm{12}}\:\:\geqslant\:\mathrm{0} \\ $$$${or} \\ $$$$\mathrm{1}+\frac{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{xy}}}{\mathrm{3}}−\left(\boldsymbol{{x}}+\boldsymbol{{y}}\right) \\ $$$$\:\:\:\:\:\:\:=\:\left(\frac{\boldsymbol{{x}}+\boldsymbol{{y}}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\left(\boldsymbol{{x}}−\boldsymbol{{y}}\right)^{\mathrm{2}} }{\mathrm{12}}\:\geqslant\:\mathrm{0}\:. \\ $$

Commented by Mr Chheang Chantria last updated on 11/Apr/17

Good Solution. Thanks you

$$\boldsymbol{{Good}}\:\boldsymbol{{Solution}}.\:\boldsymbol{{Thanks}}\:\boldsymbol{{you}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com