
Question and Answers Forum
Question Number 120427 by bramlexs22 last updated on 31/Oct/20
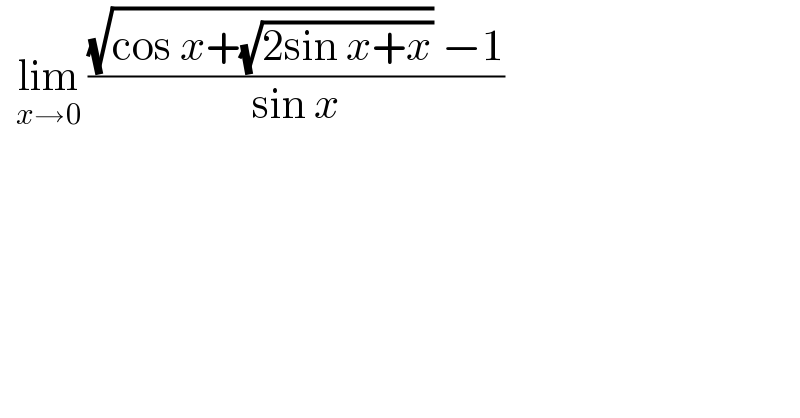
Answered by john santu last updated on 31/Oct/20
![lim_(x→0) (((√(cos x+(√(2sin x+x))))−1)/(sin x)) = lim_(x→0) (1/( (√(cos x+(√(2sin x+x))))+1)) .lim_(x→0) ((cos x−1+(√(2sin x+x)))/(sin x)) (1/2).lim_(x→0) ((−2sin^2 (x/2)+(√(2sin x+x)))/(2sin (x/2)cos (x/2))) (1/2).[lim_(x→0) −tan ((x/2))+lim_(x→0) (√((2sin x+x)/(sin^2 x))) ] = (1/2). [ 0 +lim_(x→0) (√(3/x)) ] = ∞](Q120430.png)
Answered by mathmax by abdo last updated on 31/Oct/20
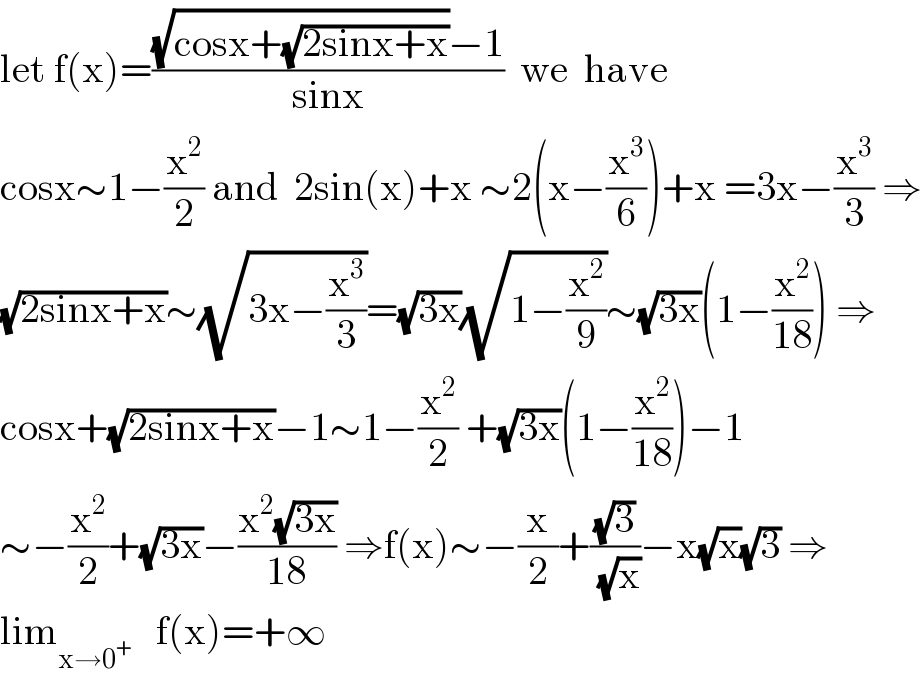
| ||
Question and Answers Forum | ||
Question Number 120427 by bramlexs22 last updated on 31/Oct/20 | ||
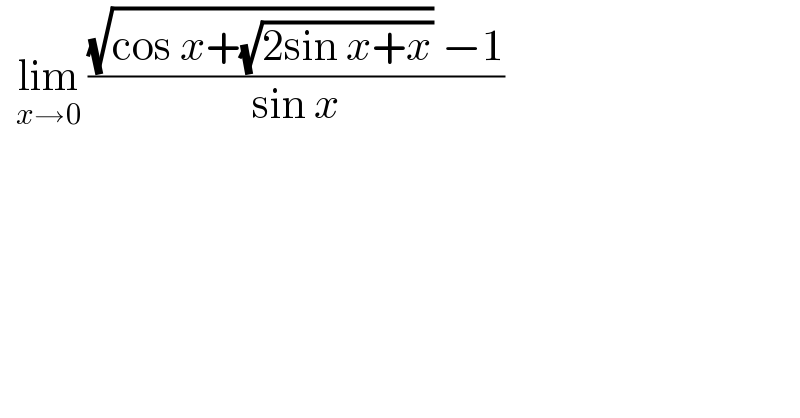 | ||
Answered by john santu last updated on 31/Oct/20 | ||
![lim_(x→0) (((√(cos x+(√(2sin x+x))))−1)/(sin x)) = lim_(x→0) (1/( (√(cos x+(√(2sin x+x))))+1)) .lim_(x→0) ((cos x−1+(√(2sin x+x)))/(sin x)) (1/2).lim_(x→0) ((−2sin^2 (x/2)+(√(2sin x+x)))/(2sin (x/2)cos (x/2))) (1/2).[lim_(x→0) −tan ((x/2))+lim_(x→0) (√((2sin x+x)/(sin^2 x))) ] = (1/2). [ 0 +lim_(x→0) (√(3/x)) ] = ∞](Q120430.png) | ||
| ||
Answered by mathmax by abdo last updated on 31/Oct/20 | ||
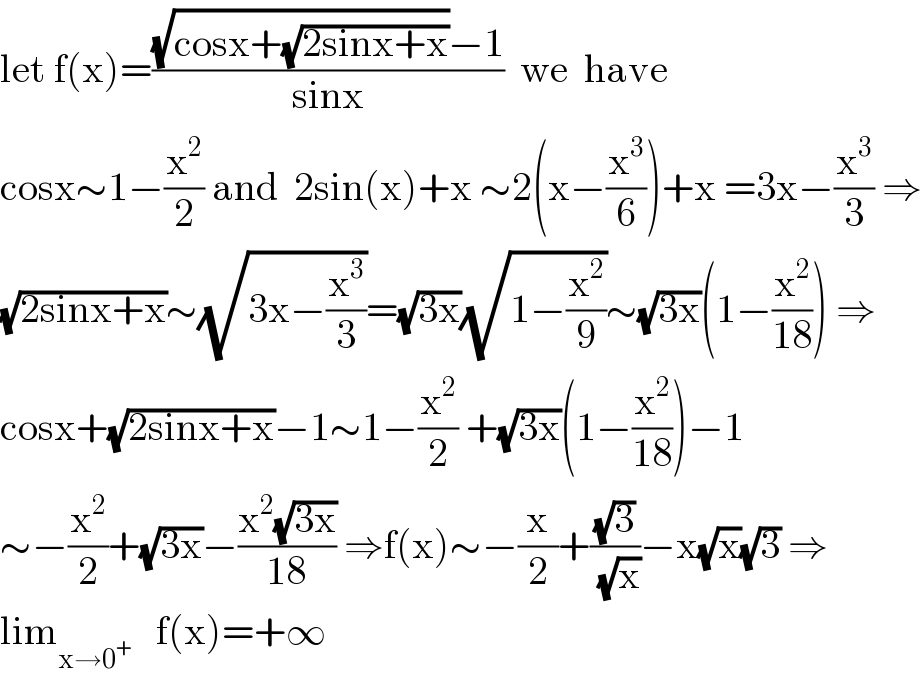 | ||
| ||