Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 120553 by snipers237 last updated on 01/Nov/20

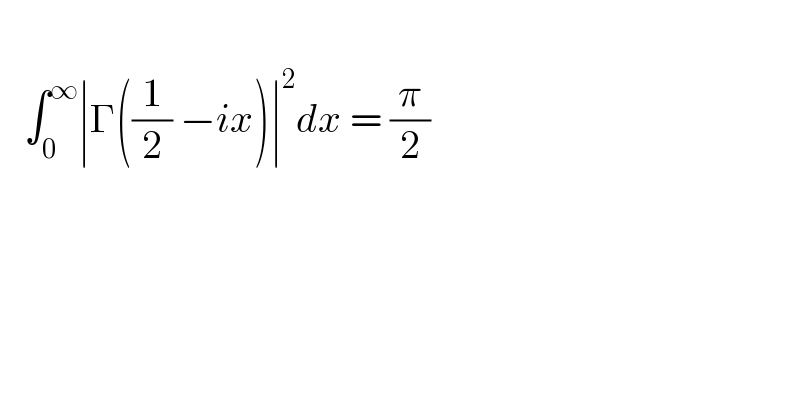
∫_0 ^∞ ∣Γ((1/2) −ix)∣^2 dx = (π/2)

$$\:\: \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\infty} \mid\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\:−{ix}\right)\mid^{\mathrm{2}} {dx}\:=\:\frac{\pi}{\mathrm{2}}\: \\ $$

Answered by mnjuly1970 last updated on 01/Nov/20

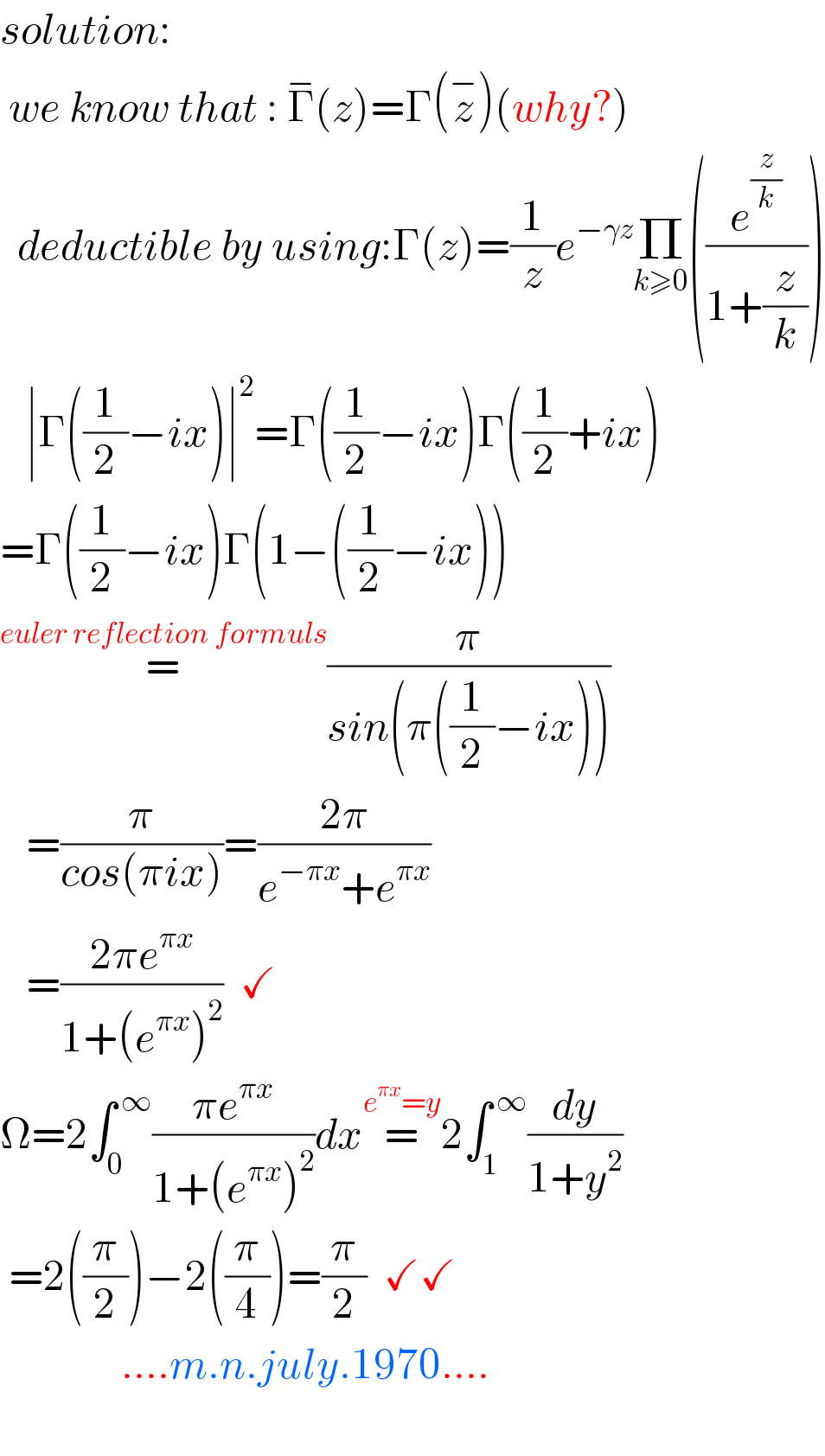
solution: we know that : Γ^− (z)=Γ(z^− )(why?) deductible by using:Γ(z)=(1/z)e^(−γz) Π_(k≥0) ((e^(z/k) /(1+(z/k)))) ∣Γ((1/2)−ix)∣^2 =Γ((1/2)−ix)Γ((1/2)+ix) =Γ((1/2)−ix)Γ(1−((1/2)−ix)) =^(euler reflection formuls) (π/(sin(π((1/2)−ix)))) =(π/(cos(πix)))=((2π)/(e^(−πx) +e^(πx) )) =((2πe^(πx) )/(1+(e^(πx) )^2 )) ✓ Ω=2∫_0 ^( ∞) ((πe^(πx) )/(1+(e^(πx) )^2 ))dx=^(e^(πx) =y) 2∫_1 ^( ∞) (dy/(1+y^2 )) =2((π/2))−2((π/4))=(π/2) ✓✓ ....m.n.july.1970....

$${solution}:\: \\ $$$$\:{we}\:{know}\:{that}\::\:\overset{−} {\Gamma}\left({z}\right)=\Gamma\left(\overset{−} {{z}}\right)\left({why}?\right) \\ $$$$\:\:{deductible}\:{by}\:{using}:\Gamma\left({z}\right)=\frac{\mathrm{1}}{{z}}{e}^{−\gamma{z}} \underset{{k}\geqslant\mathrm{0}} {\prod}\left(\frac{{e}^{\frac{{z}}{{k}}} }{\mathrm{1}+\frac{{z}}{{k}}}\right) \\ $$$$\:\:\:\mid\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\mid^{\mathrm{2}} =\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+{ix}\right) \\ $$$$=\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\Gamma\left(\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\right) \\ $$$$\overset{{euler}\:{reflection}\:{formuls}} {=}\frac{\pi}{{sin}\left(\pi\left(\frac{\mathrm{1}}{\mathrm{2}}−{ix}\right)\right)} \\ $$$$\:\:\:=\frac{\pi}{{cos}\left(\pi{ix}\right)}=\frac{\mathrm{2}\pi}{{e}^{−\pi{x}} +{e}^{\pi{x}} } \\ $$$$\:\:\:=\frac{\mathrm{2}\pi{e}^{\pi{x}} }{\mathrm{1}+\left({e}^{\pi{x}} \right)^{\mathrm{2}} }\:\:\checkmark \\ $$$$\Omega=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\pi{e}^{\pi{x}} }{\mathrm{1}+\left({e}^{\pi{x}} \right)^{\mathrm{2}} }{dx}\overset{{e}^{\pi{x}} ={y}} {=}\mathrm{2}\int_{\mathrm{1}} ^{\:\infty} \frac{{dy}}{\mathrm{1}+{y}^{\mathrm{2}} } \\ $$$$\:=\mathrm{2}\left(\frac{\pi}{\mathrm{2}}\right)−\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right)=\frac{\pi}{\mathrm{2}}\:\:\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:....{m}.{n}.{july}.\mathrm{1970}.... \\ $$$$ \\ $$

Commented by snipers237 last updated on 01/Nov/20

Γ(z) is not always equal to Γ(z^− ) but Γ^− (z)=Γ(z^− ) it′s true Γ(z)=∫_0 ^∞ t^(z−1) e^(−t) dt=∫_0 ^∞ e^((re(z)−1+iIm(z))lnt−t) dt Γ(z)=∫_0 ^∞ e^(re(z)−1−t) [cos(Im(z)lnt)+i sin(Im(z)lnt)]dt LFYTC

$$\Gamma\left({z}\right)\:{is}\:{not}\:{always}\:{equal}\:{to}\:\Gamma\left(\overset{−} {{z}}\right) \\ $$$${but}\:\:\overset{−} {\Gamma}\left({z}\right)=\Gamma\left(\overset{−} {{z}}\right)\:\:\:{it}'{s}\:{true} \\ $$$$\Gamma\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {t}^{{z}−\mathrm{1}} {e}^{−{t}} {dt}=\int_{\mathrm{0}} ^{\infty} {e}^{\left({re}\left({z}\right)−\mathrm{1}+{iIm}\left({z}\right)\right){lnt}−{t}} {dt} \\ $$$$\Gamma\left({z}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{{re}\left({z}\right)−\mathrm{1}−{t}} \left[{cos}\left({Im}\left({z}\right){lnt}\right)+{i}\:{sin}\left({Im}\left({z}\right){lnt}\right)\right]{dt} \\ $$$${LFYTC} \\ $$

Commented by mnjuly1970 last updated on 01/Nov/20

you are right i corrected it. thank you.

$${you}\:{are}\:{right}\: \\ $$$${i}\:{corrected}\:{it}. \\ $$$${thank}\:{you}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com