
Question and Answers Forum
Question Number 120758 by bramlexs22 last updated on 02/Nov/20
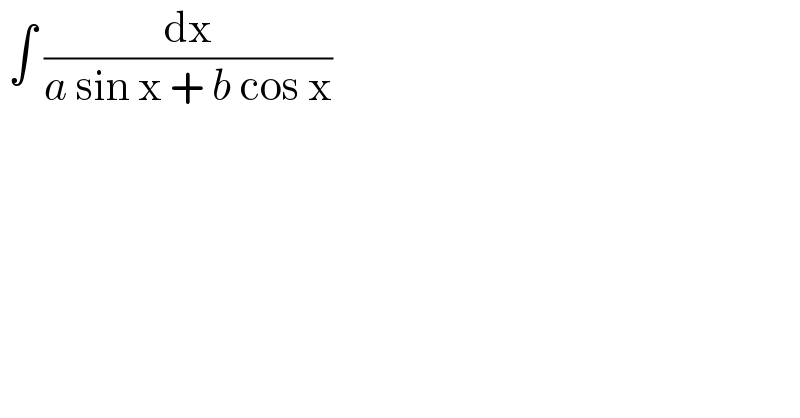
Answered by Dwaipayan Shikari last updated on 02/Nov/20
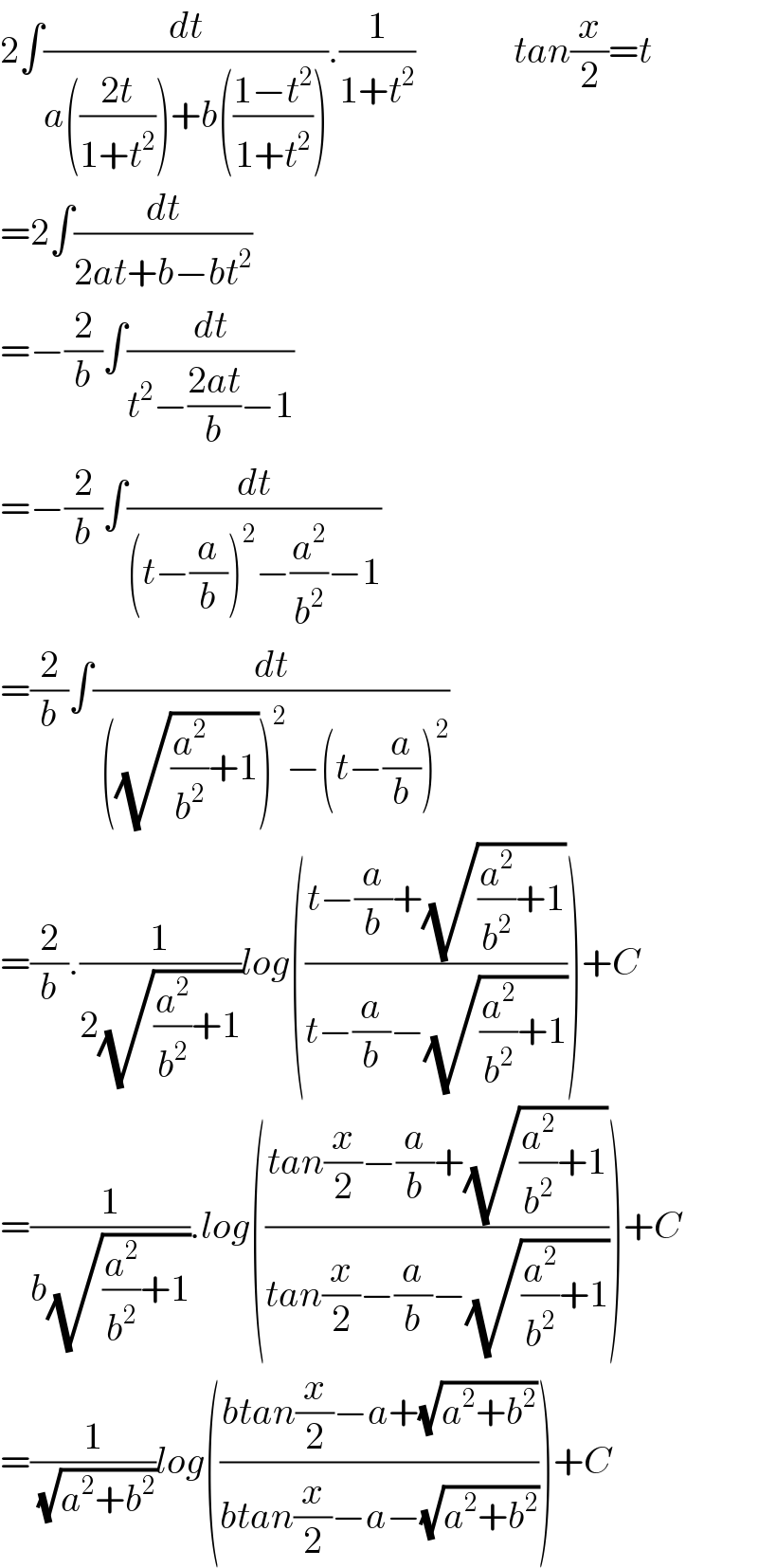
Answered by liberty last updated on 02/Nov/20
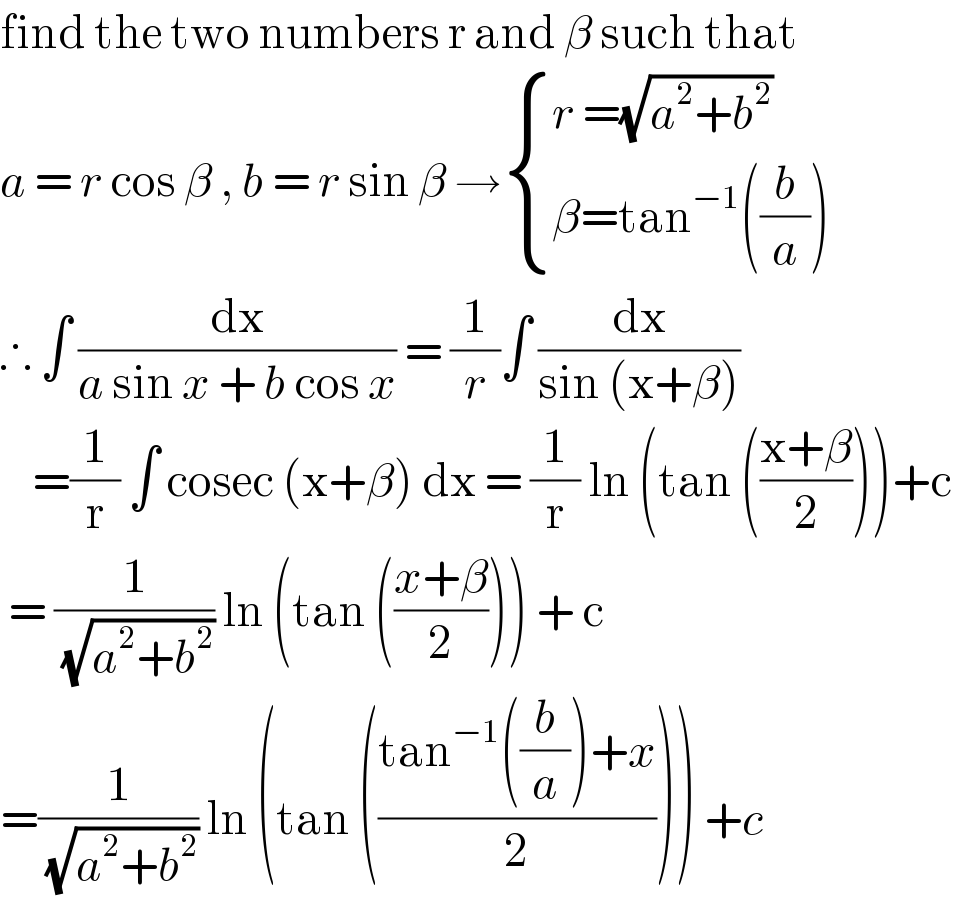
Answered by 675480065 last updated on 02/Nov/20
![asinx+bcosx=a(((2t)/(1+t^2 )))+b(((1−t^2 )/(1+t^2 ))) t=tan((x/2))⇒2dt=sec^2 ((x/2))dx ⇒dx=((2dt)/(1+t^2 )) I = ∫((2dt)/((1+t^2 ))).(((1+t^2 ))/(2at+b(1−t^2 ))) = 2∫(dt/((2at−bt^2 +b))) I = −2∫(dt/((bt^2 −2at−b))) =−2∫(dt/(b(t^2 −2at−b+(a)^2 −(a^2 )))) ⇒ I = −2∫(dt/(b[(t−a)^2 −(a^2 +b)])) ⇒ I = −(2/b)∫(dt/((t−a)^2 −(√((a^2 +b)^2 )))) Let (t−a)=(√(a^2 +b)) tanhβ ⇒dt = (√(a^2 +b)) sech^2 βdβ ⇒ I = −(2/b)∫(((√(a^2 +b)) sech^2 βdβ)/( (√((a^2 +b)^2 ))(tanh^2 β−1))) ⇒ I = −(2/(b(√(a^2 +b))))∫dβ = −2((1/(b(√(a^2 +b)))))tanh^(−1) (((t−a)/( (√(a^2 +b))))) + k ⇒ I = −(1/(b(√(a^2 +b))))ln∣((t−a+(√(a^2 +b)))/(t−a−(√(a^2 +b))))∣ + k](Q120763.png)
| ||
Question and Answers Forum | ||
Question Number 120758 by bramlexs22 last updated on 02/Nov/20 | ||
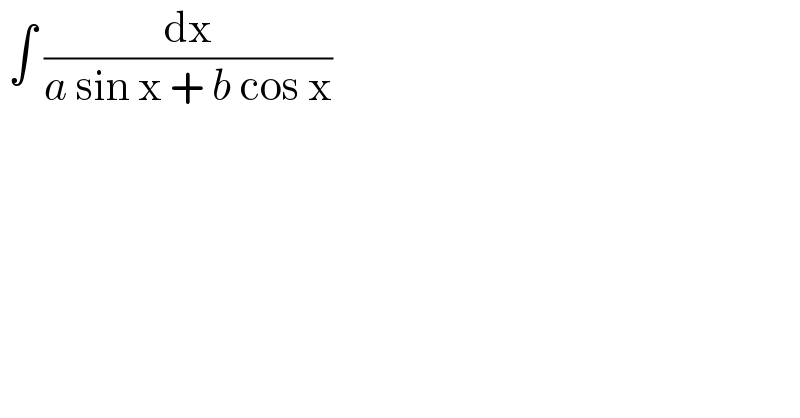 | ||
Answered by Dwaipayan Shikari last updated on 02/Nov/20 | ||
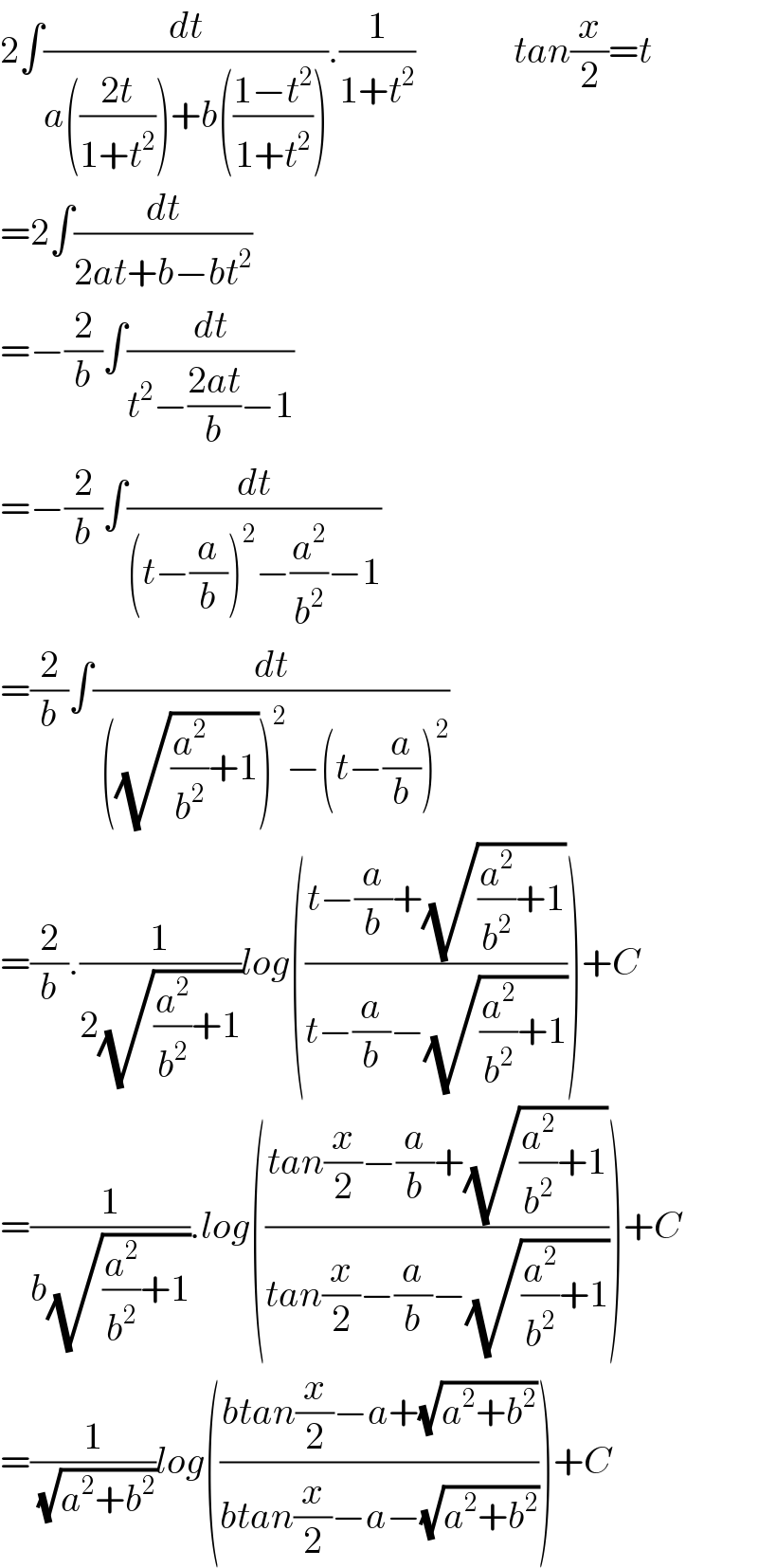 | ||
| ||
Answered by liberty last updated on 02/Nov/20 | ||
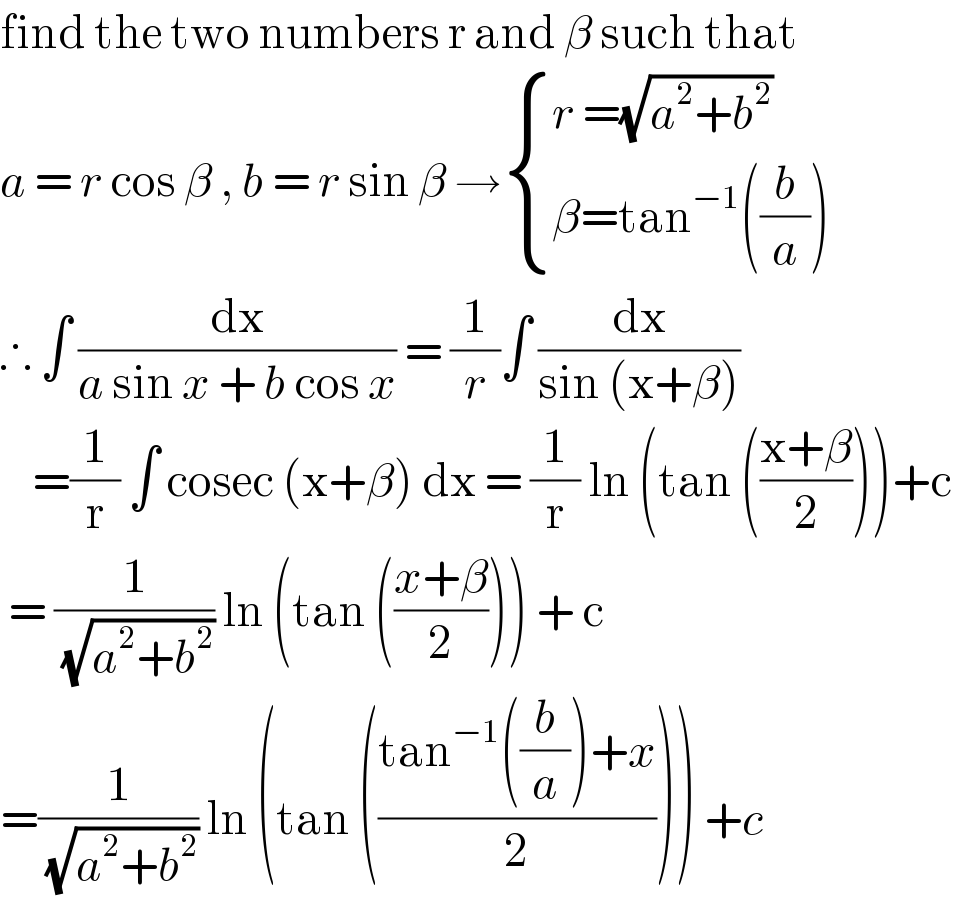 | ||
| ||
Answered by 675480065 last updated on 02/Nov/20 | ||
![asinx+bcosx=a(((2t)/(1+t^2 )))+b(((1−t^2 )/(1+t^2 ))) t=tan((x/2))⇒2dt=sec^2 ((x/2))dx ⇒dx=((2dt)/(1+t^2 )) I = ∫((2dt)/((1+t^2 ))).(((1+t^2 ))/(2at+b(1−t^2 ))) = 2∫(dt/((2at−bt^2 +b))) I = −2∫(dt/((bt^2 −2at−b))) =−2∫(dt/(b(t^2 −2at−b+(a)^2 −(a^2 )))) ⇒ I = −2∫(dt/(b[(t−a)^2 −(a^2 +b)])) ⇒ I = −(2/b)∫(dt/((t−a)^2 −(√((a^2 +b)^2 )))) Let (t−a)=(√(a^2 +b)) tanhβ ⇒dt = (√(a^2 +b)) sech^2 βdβ ⇒ I = −(2/b)∫(((√(a^2 +b)) sech^2 βdβ)/( (√((a^2 +b)^2 ))(tanh^2 β−1))) ⇒ I = −(2/(b(√(a^2 +b))))∫dβ = −2((1/(b(√(a^2 +b)))))tanh^(−1) (((t−a)/( (√(a^2 +b))))) + k ⇒ I = −(1/(b(√(a^2 +b))))ln∣((t−a+(√(a^2 +b)))/(t−a−(√(a^2 +b))))∣ + k](Q120763.png) | ||
| ||