
Question and Answers Forum
Question Number 120761 by bramlexs22 last updated on 02/Nov/20
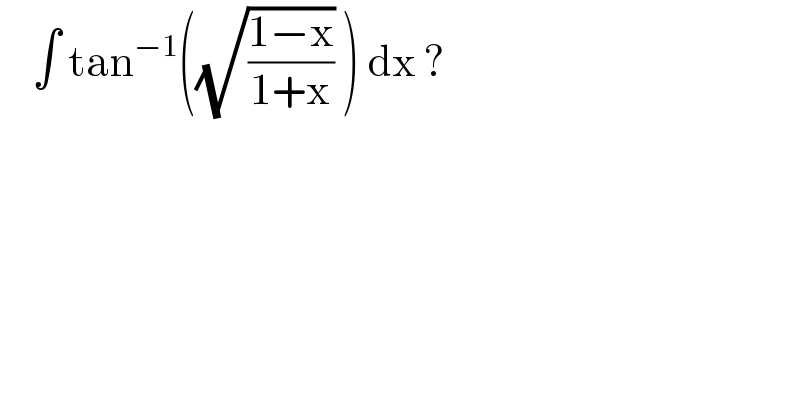
Answered by liberty last updated on 02/Nov/20
![We put x = cos ψ ⇒dx = −sin ψ dψ ∫ tan^(−1) (√((1−cos ψ)/(1+cos ψ))) (−sin ψ dψ) = ∫ tan^(−1) (√((2sin^2 (ψ/2))/(2cos^2 (ψ/2)))) (−sin ψ dψ )= ∫ tan^(−1) (tan (ψ/2))(−sin ψ dψ) = ∫ −((ψ/2))sin ψ dψ = −(1/2)[ −ψ cos ψ+sin ψ ] +c =−(1/2)[ −x cos^(−1) (x)+(√(1−x^2 )) ] + c](Q120762.png)
| ||
Question and Answers Forum | ||
Question Number 120761 by bramlexs22 last updated on 02/Nov/20 | ||
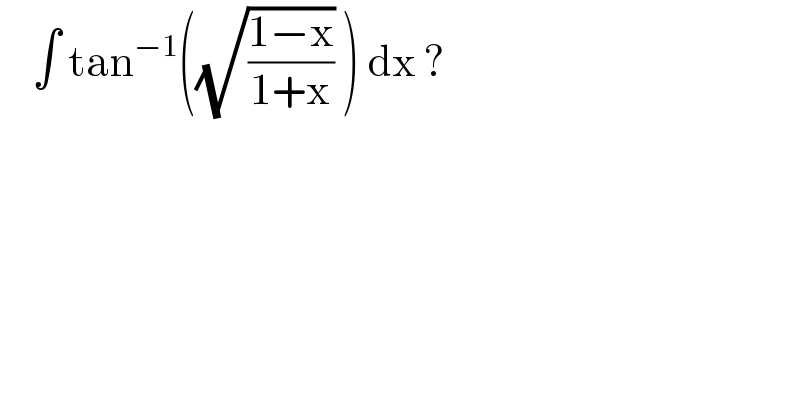 | ||
Answered by liberty last updated on 02/Nov/20 | ||
![We put x = cos ψ ⇒dx = −sin ψ dψ ∫ tan^(−1) (√((1−cos ψ)/(1+cos ψ))) (−sin ψ dψ) = ∫ tan^(−1) (√((2sin^2 (ψ/2))/(2cos^2 (ψ/2)))) (−sin ψ dψ )= ∫ tan^(−1) (tan (ψ/2))(−sin ψ dψ) = ∫ −((ψ/2))sin ψ dψ = −(1/2)[ −ψ cos ψ+sin ψ ] +c =−(1/2)[ −x cos^(−1) (x)+(√(1−x^2 )) ] + c](Q120762.png) | ||
| ||