
Question and Answers Forum
Question Number 120774 by mnjuly1970 last updated on 02/Nov/20
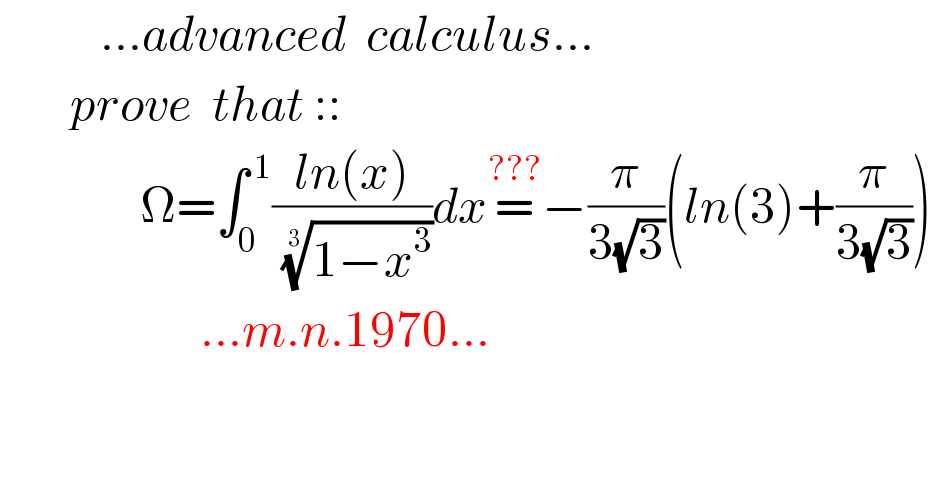
Answered by mindispower last updated on 02/Nov/20
![let x^3 =t⇒dx=t^(−2(1/3)) (dt/3) ⇒Ω=(1/3)∫_0 ^1 ((ln(t^(1/3) ))/((1−t)^(1/3) )).t^(−2(1/3)) (dt/3) Ω=(1/9)∫_0 ^1 (1−t)^(−(1/3)) t^(−2(1/3)) ln(t)dt ln(t)=(∂/∂a)x^a ∣_(x=0) Ω=∂_a (1/9)∫_0 ^1 (1−t)^(1/3) t^(−(2/3)+a) dt 9Ω=(∂/∂a)β((2/3),(1/3)+a)∣_(a=0) (∂/∂y)β(x,y)=β(x,y)[Ψ(y)−Ψ(x+y)] (∂β/∂a)=β((2/3) ,(1/3)+a)[Ψ((1/3) +a)−Ψ(1+a)] 9Ω=β((1/3),(2/3))[Ψ((1/3))−Ψ(1)] Gausse theorem Ψ((p/q))=−γ−ln(2q)−(π/2)cot(((pπ)/q))+2Σ_(n=1) ^([((q−1)/2)]) cos(((2πnp)/q))ln(sin(((nπ)/q))) Ψ((1/3))=−γ−ln(6)−(π/2).(1/( (√3)))−ln(((√3)/2)) =−γ−ln(3(√3))−(π/(2(√3))) Ψ(1)=−γ β((1/3),(2/3))=((Γ((1/3))Γ((2/3)))/(Γ(2)))=.Γ((1/3))Γ((2/3))=(π/(sin((π/3)))) =((2π)/( (√3))) 9Ω=((2π)/( (√3)))(−γ−ln(3(√3))−(π/(2(√3)))+γ) =((2π)/( (√3)))(−ln(3(√3))−(π/(2(√3)))) Ω=−(π/(27))(−(√3)ln(27)−π)=−(π/(27))(π+(√3) ln(27))](Q120792.png)
Commented by mnjuly1970 last updated on 03/Nov/20

Commented by mindispower last updated on 03/Nov/20
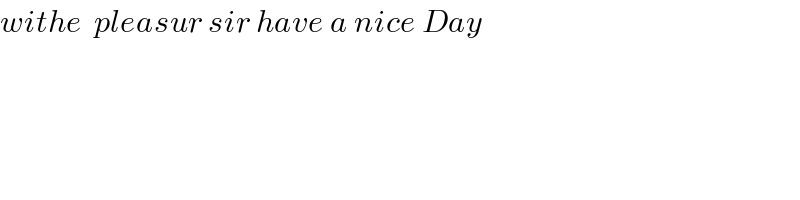
| ||
Question and Answers Forum | ||
Question Number 120774 by mnjuly1970 last updated on 02/Nov/20 | ||
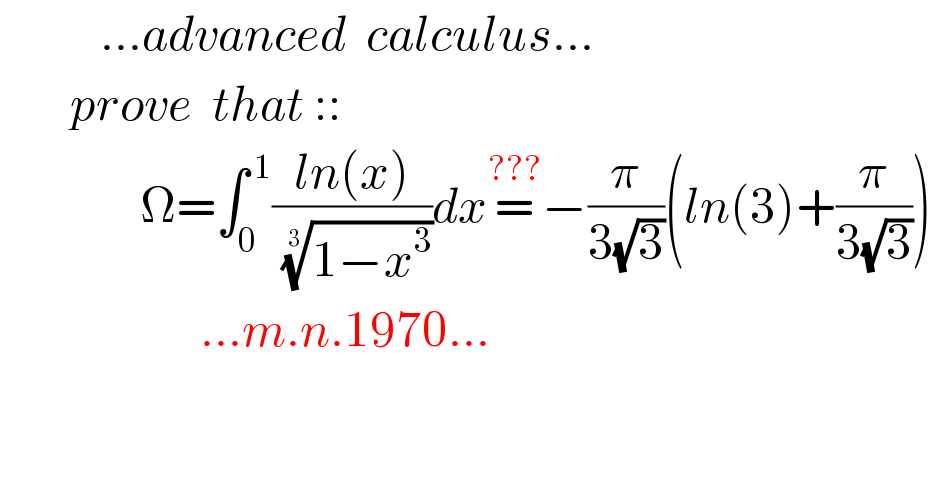 | ||
Answered by mindispower last updated on 02/Nov/20 | ||
![let x^3 =t⇒dx=t^(−2(1/3)) (dt/3) ⇒Ω=(1/3)∫_0 ^1 ((ln(t^(1/3) ))/((1−t)^(1/3) )).t^(−2(1/3)) (dt/3) Ω=(1/9)∫_0 ^1 (1−t)^(−(1/3)) t^(−2(1/3)) ln(t)dt ln(t)=(∂/∂a)x^a ∣_(x=0) Ω=∂_a (1/9)∫_0 ^1 (1−t)^(1/3) t^(−(2/3)+a) dt 9Ω=(∂/∂a)β((2/3),(1/3)+a)∣_(a=0) (∂/∂y)β(x,y)=β(x,y)[Ψ(y)−Ψ(x+y)] (∂β/∂a)=β((2/3) ,(1/3)+a)[Ψ((1/3) +a)−Ψ(1+a)] 9Ω=β((1/3),(2/3))[Ψ((1/3))−Ψ(1)] Gausse theorem Ψ((p/q))=−γ−ln(2q)−(π/2)cot(((pπ)/q))+2Σ_(n=1) ^([((q−1)/2)]) cos(((2πnp)/q))ln(sin(((nπ)/q))) Ψ((1/3))=−γ−ln(6)−(π/2).(1/( (√3)))−ln(((√3)/2)) =−γ−ln(3(√3))−(π/(2(√3))) Ψ(1)=−γ β((1/3),(2/3))=((Γ((1/3))Γ((2/3)))/(Γ(2)))=.Γ((1/3))Γ((2/3))=(π/(sin((π/3)))) =((2π)/( (√3))) 9Ω=((2π)/( (√3)))(−γ−ln(3(√3))−(π/(2(√3)))+γ) =((2π)/( (√3)))(−ln(3(√3))−(π/(2(√3)))) Ω=−(π/(27))(−(√3)ln(27)−π)=−(π/(27))(π+(√3) ln(27))](Q120792.png) | ||
| ||
Commented by mnjuly1970 last updated on 03/Nov/20 | ||
 | ||
Commented by mindispower last updated on 03/Nov/20 | ||
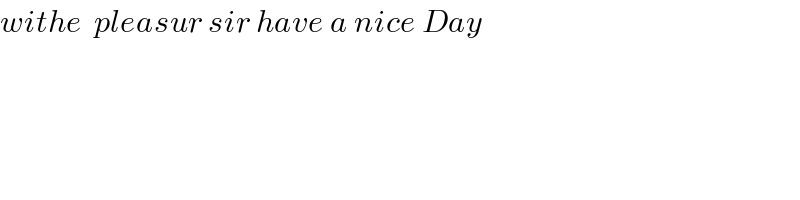 | ||