Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 120775 by mnjuly1970 last updated on 02/Nov/20

$$...advancedcalculus...$$$$evaluate::$$$$\mathrm{\Phi }\stackrel{???}{=}{\int }_0^{1}ln\left(x\right){tan}^{-1}\left(x\right)dx$$$$...m.n.1970...$$

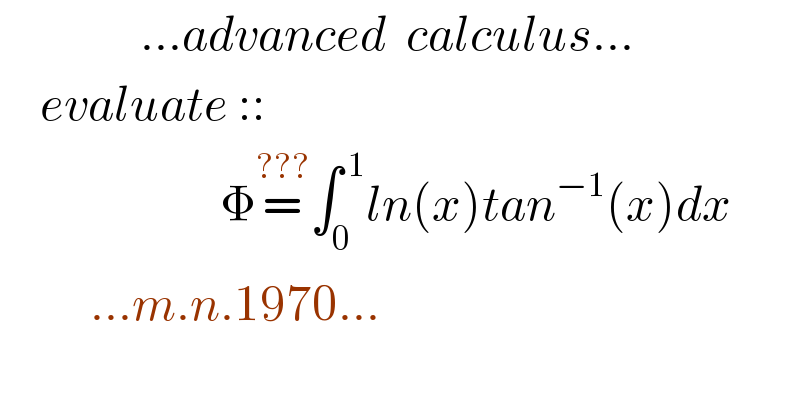
Answered by Dwaipayan Shikari last updated on 02/Nov/20

$$\int {tan}^{-1}xdx$$$$={xtan}^{-1}x-\int \frac{x}{1+x^2}$$$$={xtan}^{-1}x-log\left(\sqrt{1+x^2}\right)(logx{\int }_0^1{tan}^{-1}\left(x\right)dx=0)$$$$\mathrm{\Phi }=\left[log\left(x\right){\int }_0^1{tan}^{-1}x\right]-{\int }_0^1{tan}^{-1}x+\frac{1}{2}{\int }_0^1\frac{log(1+x^2)}{x}$$$$\mathrm{\Phi }=-[{xtan}^{-1}x-log\left(\sqrt{1+x^2}\right)]+\frac{1}{2}{\int }_0^1\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^{n+1}{x}^{2n-1}.\frac{1}{n}$$$$\mathrm{\Phi }=-\frac{\pi }{4}+\frac{1}{2}log\left(2\right)+\frac{1}{2}\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^{n+1}{\int }_0^1{x}^{2n-1}.\frac{1}{n}dx$$$$\mathrm{\Phi }=-\frac{\pi }{4}+\frac{1}{2}log\left(2\right)+\frac{1}{2}\underset{n=1}{\sum ^{\mathrm{\infty }}}{(-1)}^{n+1}\frac{1}{2n^2}$$$$\mathrm{\Phi }=-\frac{\pi }{4}+\frac{1}{2}log\left(2\right)+\frac{{\pi }^2}{48}$$

Commented by mnjuly1970 last updated on 02/Nov/20

$$thankyousomuchmrdwaipayanexcellent$$

Commented by Dwaipayan Shikari last updated on 03/Nov/20

$$Withpleasure$$

Answered by mindispower last updated on 02/Nov/20

$$={\left[(xln\left(x\right)-x){tan}^{-}\left(x\right)\right]}_0^1-{\int }_0^1\frac{xln\left(x\right)-x}{1+x^2}dx$$$$=-{tan}^{-}\left(1\right)+{\int }_0^1\frac{x}{1+x^2}dx-{\int }_0^1\frac{x}{1+x^2}ln\left(x\right)dx$$$$-\frac{\pi }{4}+\frac{ln\left(2\right)}{2}-\sum _{k⩾0}{\int }_0^1{(-1)}^k{x}^{2k+1}ln\left(x\right)dx$$$$=-\frac{\pi }{4}+\frac{ln\left(2\right)}{2}-\sum _{k⩾0}{(-1)}^k(-\frac{1}{{(2k+2)}^2})$$$$=-\frac{\pi }{4}+\frac{ln\left(2\right)}{2}+\frac{1}{4}\sum _{k⩾0}\frac{{(-1)}^k}{{(k+1)}^2}$$$$=-\frac{\pi }{4}+\frac{ln\left(2\right)}{2}+\frac{1}{4}\left[\frac{{\pi }^2}{12}\right]$$$$=\frac{-12\pi +{\pi }^2+24ln\left(2\right)}{48}$$

Commented by mnjuly1970 last updated on 02/Nov/20

$$verynicesirmindspower$$$$grateful..$$

Commented by mindispower last updated on 03/Nov/20

$$thanxwithepleasurnicedaysir$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com