
Question Number 12098 by Nayon last updated on 13/Apr/17
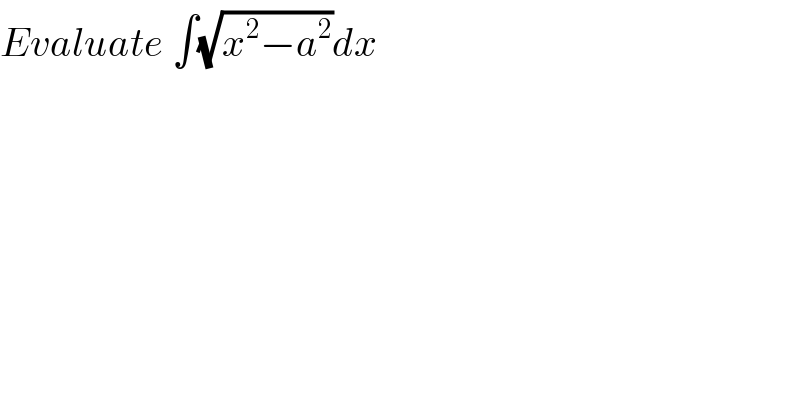
$${Evaluate}\:\int\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx} \\ $$$$ \\ $$$$ \\ $$
Answered by sma3l2996 last updated on 13/Apr/17
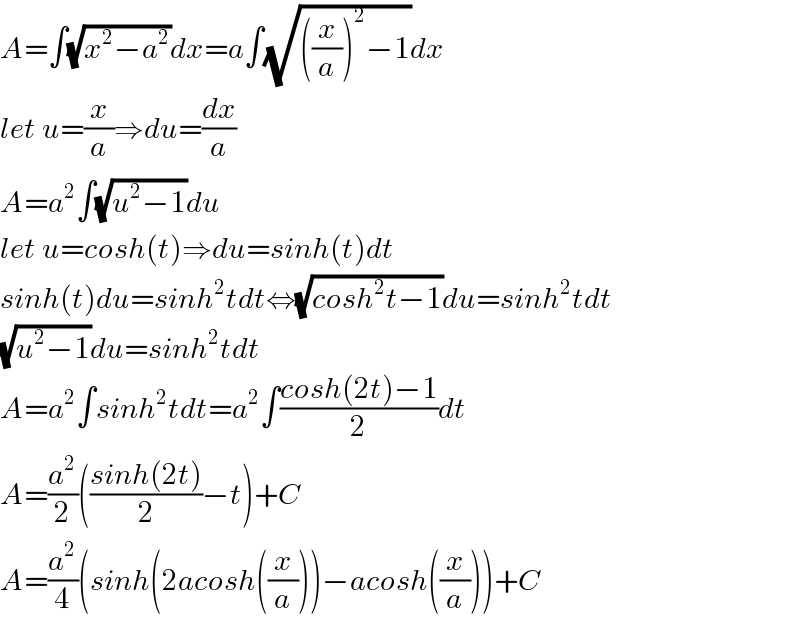
$${A}=\int\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }{dx}={a}\int\sqrt{\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} −\mathrm{1}}{dx} \\ $$$${let}\:{u}=\frac{{x}}{{a}}\Rightarrow{du}=\frac{{dx}}{{a}} \\ $$$${A}={a}^{\mathrm{2}} \int\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}{du} \\ $$$${let}\:{u}={cosh}\left({t}\right)\Rightarrow{du}={sinh}\left({t}\right){dt} \\ $$$${sinh}\left({t}\right){du}={sinh}^{\mathrm{2}} {tdt}\Leftrightarrow\sqrt{{cosh}^{\mathrm{2}} {t}−\mathrm{1}}{du}={sinh}^{\mathrm{2}} {tdt} \\ $$$$\sqrt{{u}^{\mathrm{2}} −\mathrm{1}}{du}={sinh}^{\mathrm{2}} {tdt} \\ $$$${A}={a}^{\mathrm{2}} \int{sinh}^{\mathrm{2}} {tdt}={a}^{\mathrm{2}} \int\frac{{cosh}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}{dt} \\ $$$${A}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{{sinh}\left(\mathrm{2}{t}\right)}{\mathrm{2}}−{t}\right)+{C} \\ $$$${A}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\left({sinh}\left(\mathrm{2}{acosh}\left(\frac{{x}}{{a}}\right)\right)−{acosh}\left(\frac{{x}}{{a}}\right)\right)+{C} \\ $$
Commented by Nayon last updated on 13/Apr/17

$${pls}\:{ans}\:{without}\:{using}\:{hyperbolic} \\ $$$${trig}... \\ $$$$ \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17
![x=ait,dx=aidt,i=(√(−1)) I=∫(√(−a^2 t^2 −a^2 ))aidt=−a^2 ∫(√(t^2 +1))dt= =−a^2 [t(√(t^2 +1))−∫t((2tdt)/(2(√(t^2 +1))))]= =−a^2 [t(√(t^2 +1))−∫(((t^2 +1)−1)/(√(t^2 +1)))dt]= =−a^2 [t(√(t^2 +1))−∫(√(t^2 +1))dt+∫(dt/(√(t^2 +1)))]= −a^2 t(√(t^2 +1))+a^2 ∫(√(t^2 +1))dt−(a^2 /2)ln(t+(√(t^2 +1))) 2I=−a^2 (x/(ai)).((√(x^2 −a^2 ))/(ai))−(a^2 /2)ln((x/(ai))+((√(x^2 −a^2 ))/(ai)))⇒ I=(x/2)(√(x^2 −a^2 ))−(a^2 /4)ln(x+(√(x^2 −a^2 )))+C .■ (−a^2 ×(1/(ai))×(1/(ai))=1,C=(a^2 /4)ln(ai))](Q12143.png)
$${x}={ait},{dx}={aidt},{i}=\sqrt{−\mathrm{1}} \\ $$$${I}=\int\sqrt{−{a}^{\mathrm{2}} {t}^{\mathrm{2}} −{a}^{\mathrm{2}} }{aidt}=−{a}^{\mathrm{2}} \int\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=−{a}^{\mathrm{2}} \left[{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}−\int{t}\frac{\mathrm{2}{tdt}}{\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\right]= \\ $$$$=−{a}^{\mathrm{2}} \left[{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}−\int\frac{\left({t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{1}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}{dt}\right]= \\ $$$$=−{a}^{\mathrm{2}} \left[{t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}−\int\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}+\int\frac{{dt}}{\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\right]= \\ $$$$−{a}^{\mathrm{2}} {t}\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}+{a}^{\mathrm{2}} \int\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{ln}\left({t}+\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\mathrm{2}{I}=−{a}^{\mathrm{2}} \frac{{x}}{{ai}}.\frac{\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{ai}}−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{ln}\left(\frac{{x}}{{ai}}+\frac{\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }}{{ai}}\right)\Rightarrow \\ $$$${I}=\frac{{x}}{\mathrm{2}}\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} −{a}^{\mathrm{2}} }\right)+{C}\:\:.\blacksquare \\ $$$$\left(−{a}^{\mathrm{2}} ×\frac{\mathrm{1}}{{ai}}×\frac{\mathrm{1}}{{ai}}=\mathrm{1},{C}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}{ln}\left({ai}\right)\right) \\ $$
