Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 121010 by mathocean1 last updated on 04/Nov/20

$$\mathrm{calculate}:$$$$\underset{\mathrm{x}\to 3}{\lim }\frac{\sqrt{\mathrm{x}+1}-2}{3-\sqrt{\mathrm{x}+6}}$$

Answered by 675480065 last updated on 04/Nov/20

$$=\underset{x\to 3}{\lim }\frac{\frac{1}{2\sqrt{\mathrm{x}+1}}}{-\frac{1}{2\sqrt{\mathrm{x}+6}}}=-\underset{x\to 3}{\lim }\sqrt{\frac{\mathrm{x}+6}{\mathrm{x}+1}}=-3/2$$$$$$

Commented by mathocean1 last updated on 04/Nov/20

$$\mathrm{please}\mathrm{sir}\mathrm{can}\mathrm{you}\mathrm{detail}\mathrm{the}$$$$\mathrm{first}\mathrm{expression}$$$$$$$$$$$$$$

Commented by Ar Brandon last updated on 04/Nov/20

Since on evaluating we get 0/0 we can therefore apply l'hôpital's rule by differentiating the numerator and the denominator.

Answered by Ar Brandon last updated on 04/Nov/20

$$\mathrm{{\rm Y}}=\underset{\mathrm{x}\to 3}{\lim }\frac{\sqrt{\mathrm{x}+1}-2}{3-\sqrt{\mathrm{x}+6}}$$$$=\underset{\mathrm{x}\to 3}{\lim }\frac{1}{2\sqrt{\mathrm{x}+1}}\cdot \frac{2\sqrt{\mathrm{x}+6}}{-1}$$$$=-\frac{2\sqrt{9}}{2\sqrt{4}}=-\frac{3}{2}$$

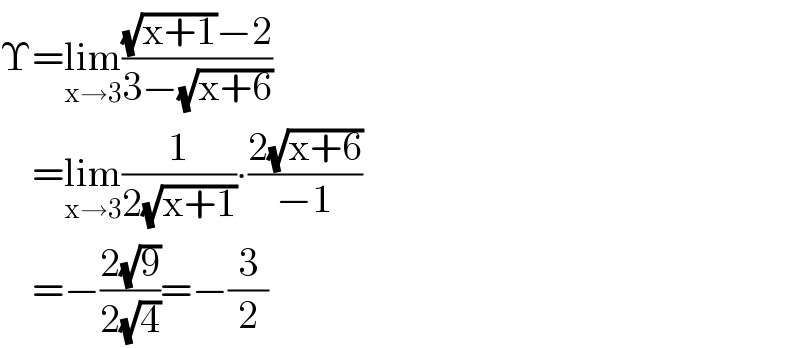
Answered by mathmax by abdo last updated on 04/Nov/20

$${\lim }_{\mathrm{x}\to 3}\frac{\sqrt{\mathrm{x}+1}-2}{3-\sqrt{\mathrm{x}+6}}$$$${\lim }_{\mathrm{x}\to 3}\frac{(\sqrt{\mathrm{x}+1}-2)(3+\sqrt{\mathrm{x}+6})(\sqrt{\mathrm{x}+1}+2)}{(3-\sqrt{\mathrm{x}+6})(3+\sqrt{\mathrm{x}+6})(\sqrt{\mathrm{x}+1}+2)}$$$$={\lim }_{\mathrm{x}\to 3}\frac{(\mathrm{x}+1-4)(3+\sqrt{\mathrm{x}+6})}{(9-\mathrm{x}-6)(\sqrt{\mathrm{x}+1}+2)}$$$$={\lim }_{\mathrm{x}\to 3}\frac{(\mathrm{x}-3)(3+\sqrt{\mathrm{x}+6})}{(3-\mathrm{x})(\sqrt{\mathrm{x}+1}+2)}$$$$={\lim }_{\mathrm{x}\to 3}-\frac{3+\sqrt{\mathrm{x}+6}}{2+\sqrt{\mathrm{x}+1}}=-\frac{6}{4}=-\frac{3}{2}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com