
Question and Answers Forum
Question Number 121042 by bramlexs22 last updated on 05/Nov/20
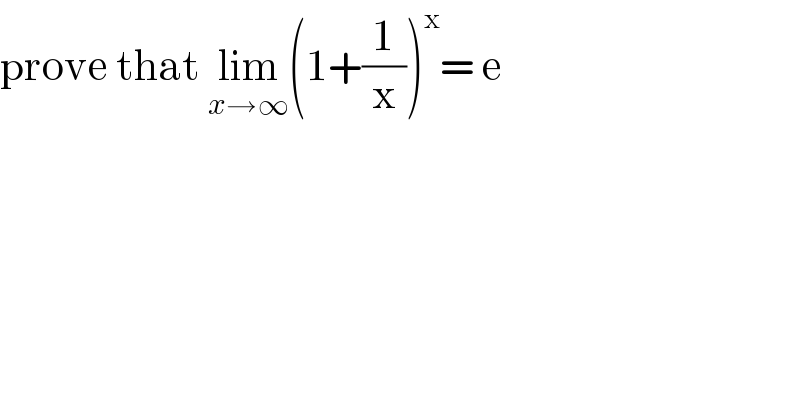
Answered by bobhans last updated on 05/Nov/20
![Let w = lim_(x→∞) (1+(1/x))^x then ln (w)= ln (lim_(x→∞) (1+(1/x))^x ) ln (w)=lim_(x→∞) (ln (1+(1/x))^x ) ln (w)= lim_(x→∞) (x.ln (1+(1/x))) ln (w)= lim_(x→∞) (x.[(1/x)−(1/(2x^2 ))+(1/(3x^3 ))−(1/(4x^4 ))+... ]) ln (w)= lim_(x→∞) (1−(1/(2x))+(1/(3x^2 ))−(1/(4x^3 ))+...) ln (w) = 1 ⇒w = e^1 = e.](Q121043.png)
Answered by Dwaipayan Shikari last updated on 05/Nov/20
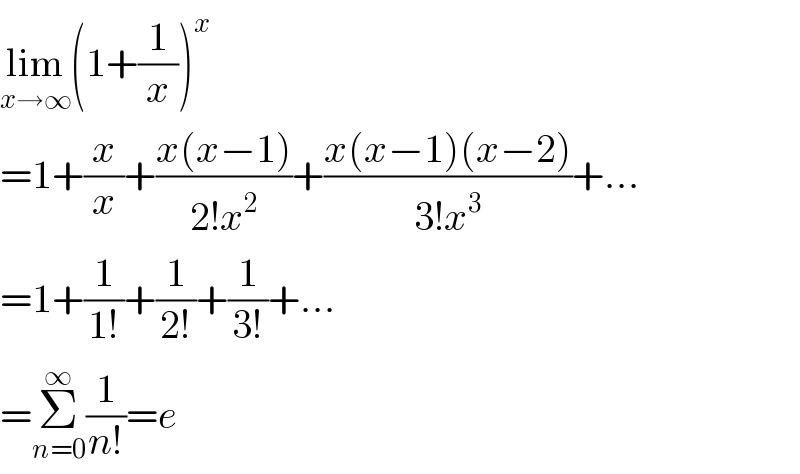
| ||
Question and Answers Forum | ||
Question Number 121042 by bramlexs22 last updated on 05/Nov/20 | ||
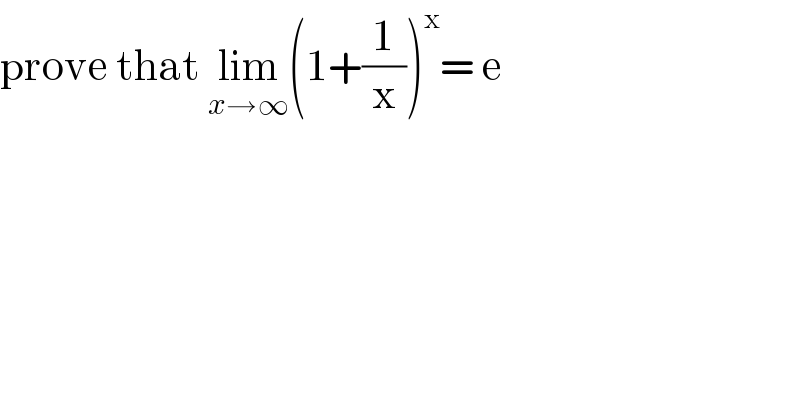 | ||
Answered by bobhans last updated on 05/Nov/20 | ||
![Let w = lim_(x→∞) (1+(1/x))^x then ln (w)= ln (lim_(x→∞) (1+(1/x))^x ) ln (w)=lim_(x→∞) (ln (1+(1/x))^x ) ln (w)= lim_(x→∞) (x.ln (1+(1/x))) ln (w)= lim_(x→∞) (x.[(1/x)−(1/(2x^2 ))+(1/(3x^3 ))−(1/(4x^4 ))+... ]) ln (w)= lim_(x→∞) (1−(1/(2x))+(1/(3x^2 ))−(1/(4x^3 ))+...) ln (w) = 1 ⇒w = e^1 = e.](Q121043.png) | ||
| ||
Answered by Dwaipayan Shikari last updated on 05/Nov/20 | ||
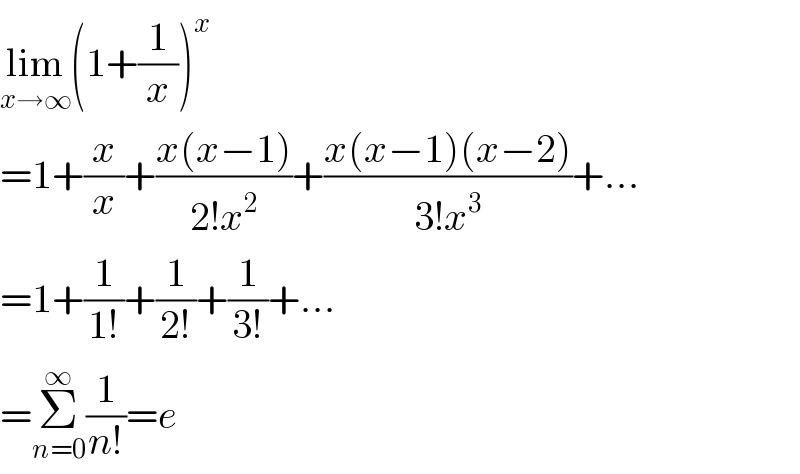 | ||
| ||