
Question and Answers Forum
Question Number 121117 by benjo_mathlover last updated on 05/Nov/20
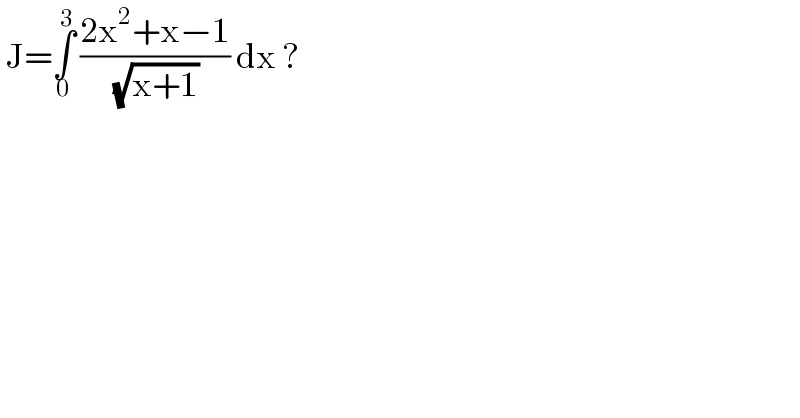
Answered by liberty last updated on 05/Nov/20
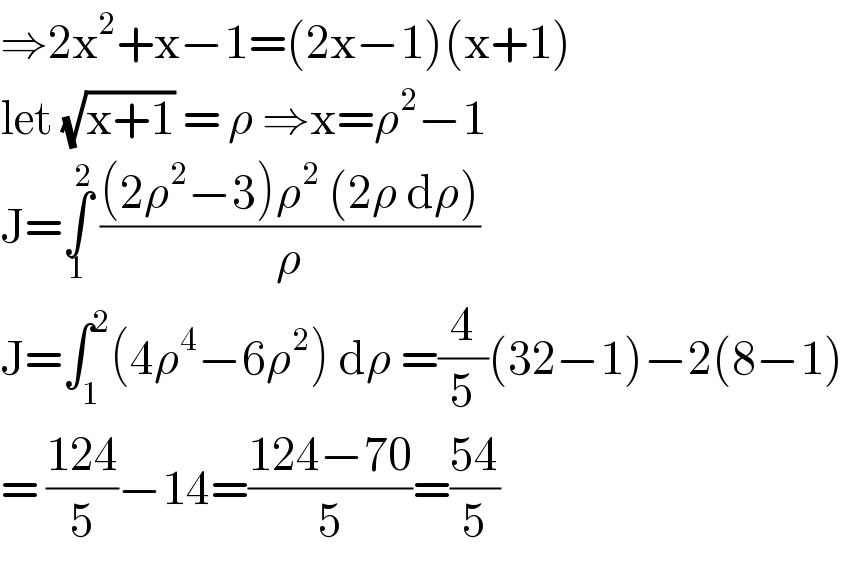
Answered by Bird last updated on 05/Nov/20
![J =∫_0 ^3 ((2x^2 +x−1)/( (√(x+1))))dx we do the changement (√(x+1))=t ⇒x+1=t^(2 ) ⇒x=t^2 −1 ⇒ J =∫_1 ^2 ((2(t^2 −1)^2 +t^2 −1−1)/t)(2t)dt =2 ∫_1 ^2 (2(t^4 −2t^2 +1)+t^2 −2)dt =2 ∫_1 ^2 (2t^4 −3t^2 )dt =4 ∫_1 ^2 t^4 dt +6 ∫_1 ^2 t^2 dt =(4/5)[t^5 ]_1 ^2 +2[t^3 ]_1 ^2 =(4/5){2^5 −1} +2{2^3 −1}](Q121198.png)
| ||
Question and Answers Forum | ||
Question Number 121117 by benjo_mathlover last updated on 05/Nov/20 | ||
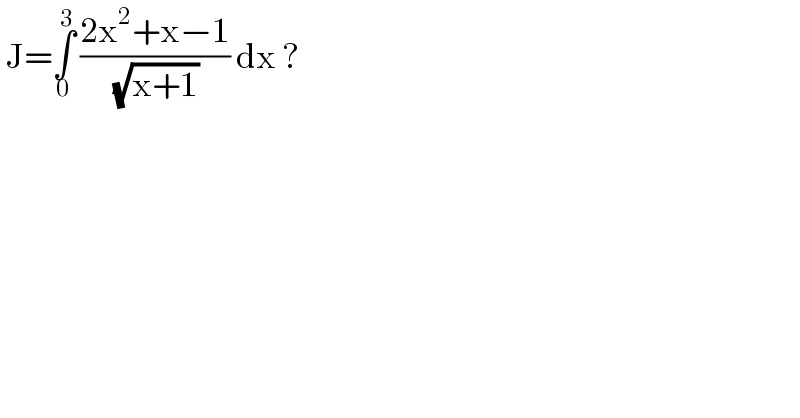 | ||
Answered by liberty last updated on 05/Nov/20 | ||
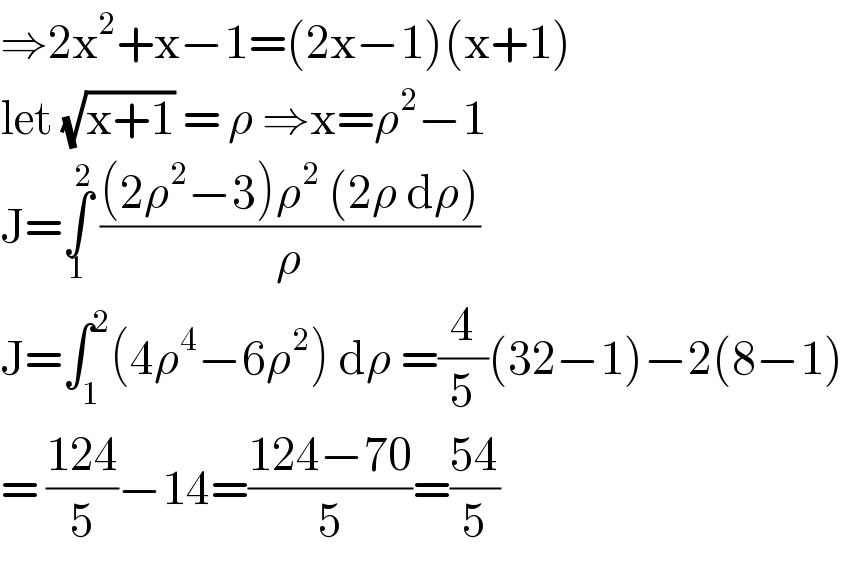 | ||
| ||
Answered by Bird last updated on 05/Nov/20 | ||
![J =∫_0 ^3 ((2x^2 +x−1)/( (√(x+1))))dx we do the changement (√(x+1))=t ⇒x+1=t^(2 ) ⇒x=t^2 −1 ⇒ J =∫_1 ^2 ((2(t^2 −1)^2 +t^2 −1−1)/t)(2t)dt =2 ∫_1 ^2 (2(t^4 −2t^2 +1)+t^2 −2)dt =2 ∫_1 ^2 (2t^4 −3t^2 )dt =4 ∫_1 ^2 t^4 dt +6 ∫_1 ^2 t^2 dt =(4/5)[t^5 ]_1 ^2 +2[t^3 ]_1 ^2 =(4/5){2^5 −1} +2{2^3 −1}](Q121198.png) | ||
| ||