
Question and Answers Forum
Question Number 121203 by benjo_mathlover last updated on 05/Nov/20
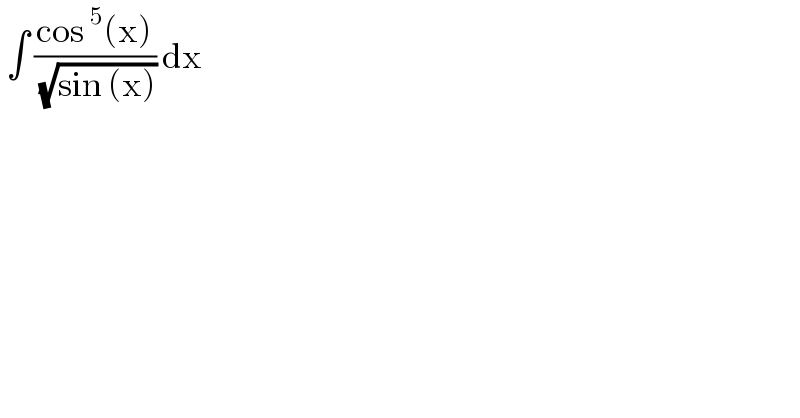
Answered by MJS_new last updated on 06/Nov/20
![∫((cos^5 x)/( (√(sin x))))dx= [t=(√(sin x)) → dx=((2(√(sin x)))/(cos x))dt] =2∫(t^4 −1)^2 dt= =(2/9)t^9 −(4/5)t^5 +2t= =2((1/9)sin^4 x −(2/5)sin^2 x +1)(√(sin x)) +C](Q121212.png)
Answered by bobhans last updated on 06/Nov/20
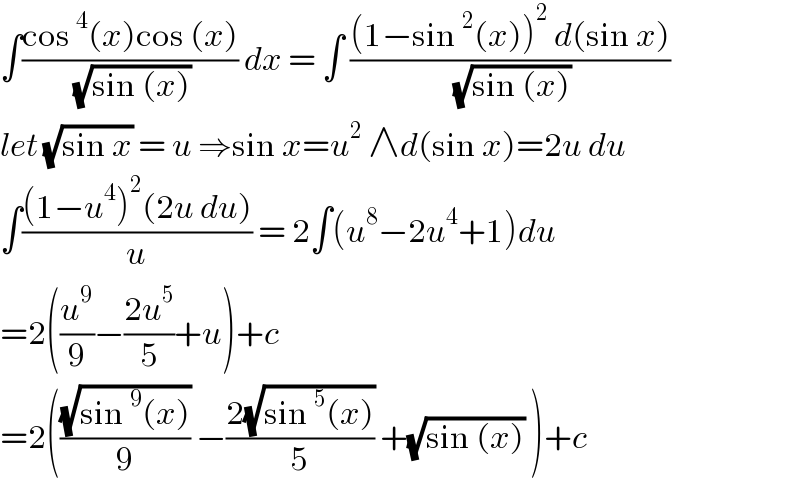
| ||
Question and Answers Forum | ||
Question Number 121203 by benjo_mathlover last updated on 05/Nov/20 | ||
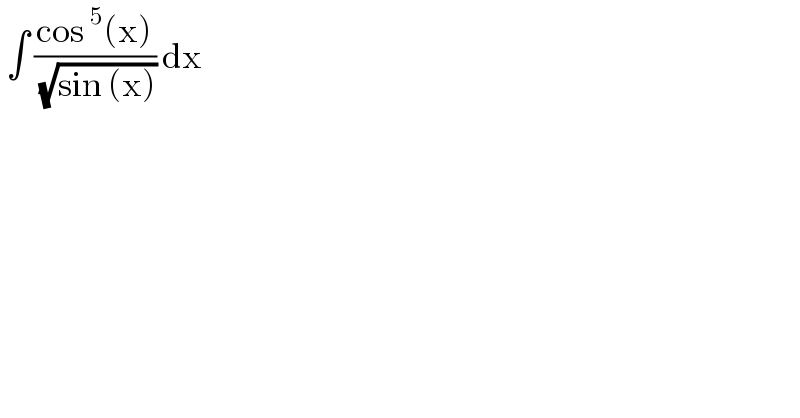 | ||
Answered by MJS_new last updated on 06/Nov/20 | ||
![∫((cos^5 x)/( (√(sin x))))dx= [t=(√(sin x)) → dx=((2(√(sin x)))/(cos x))dt] =2∫(t^4 −1)^2 dt= =(2/9)t^9 −(4/5)t^5 +2t= =2((1/9)sin^4 x −(2/5)sin^2 x +1)(√(sin x)) +C](Q121212.png) | ||
| ||
Answered by bobhans last updated on 06/Nov/20 | ||
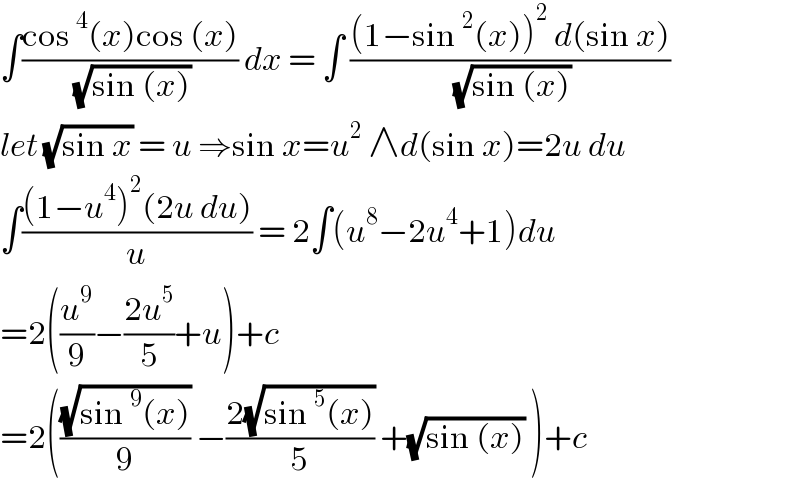 | ||
| ||