Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 122236 by benjo_mathlover last updated on 15/Nov/20

$$\underset{x\to 0}{\lim }\frac{{(1+mx)}^n-{(1+nx)}^m}{x^2}?$$

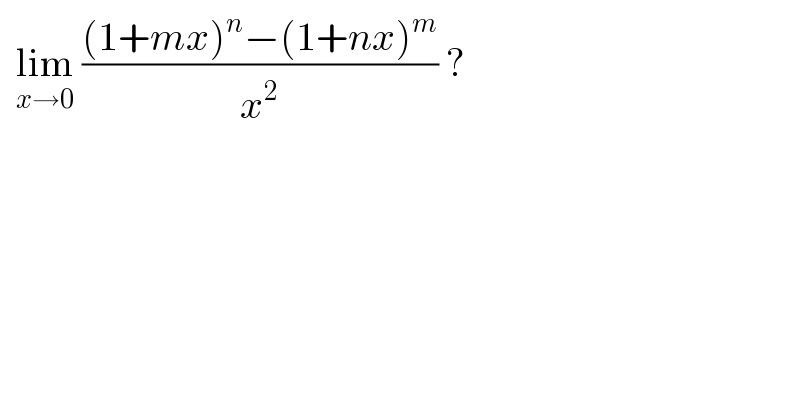
Answered by Dwaipayan Shikari last updated on 15/Nov/20

$$\underset{x\to 0}{\lim }\frac{1+mnx+\frac{n(n-1)}{2}{m}^2{x}^2-1-mnx-\frac{m(m-1)}{2}{n}^2{x}^2}{x^2}$$$$=\frac{n(n-1)m^2-m(m-1)n^2}{2}$$

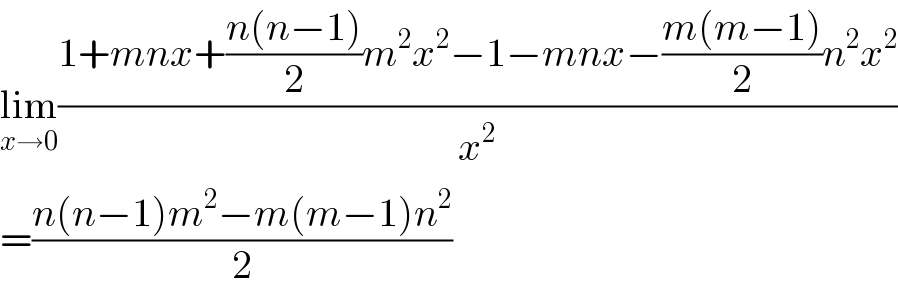
Answered by liberty last updated on 15/Nov/20

$$\underset{x\to 0}{\lim }\frac{\mathrm{mn}{(1+\mathrm{mx})}^{\mathrm{n}-1}-\mathrm{mn}{(1+\mathrm{nx})}^{\mathrm{m}-1}}{2\mathrm{x}}=$$$$\frac{\mathrm{mn}}{2}\underset{x\to 0}{\lim }\frac{{(1+\mathrm{mx})}^{\mathrm{n}-1}-{(1+\mathrm{nx})}^{\mathrm{m}-1}}{\mathrm{x}}=$$$$\frac{\mathrm{mn}}{2}\underset{x\to 0}{\lim }\frac{\mathrm{m}(\mathrm{n}-1){(1+\mathrm{mx})}^{\mathrm{n}-2}-\mathrm{n}(\mathrm{m}-1){(1+\mathrm{nx})}^{\mathrm{m}-2}}{1}=$$$$\frac{\mathrm{mn}}{2}.[\mathrm{mn}-\mathrm{m}-\mathrm{mn}+\mathrm{n}]=\frac{\mathrm{mn}(\mathrm{n}-\mathrm{m})}{2}.▴$$$$$$

Answered by mathmax by abdo last updated on 15/Nov/20

$$\mathrm{let}\mathrm{f}\left(\mathrm{x}\right)=\frac{{(1+\mathrm{mx})}^{\mathrm{n}}-{(1+\mathrm{nx})}^{\mathrm{m}}}{{\mathrm{x}}^2}\mathrm{we}\mathrm{have}$$$${(1+\mathrm{u})}^{\alpha }=1+\alpha \mathrm{u}+\frac{\alpha (\alpha -1)}{2}{\mathrm{u}}^2+\mathrm{o}\left({\mathrm{u}}^3\right)\Rightarrow$$$${(1+\mathrm{mx})}^{\mathrm{n}}\sim 1+\mathrm{nmx}+\frac{\mathrm{n}(\mathrm{n}-1)}{2}{\mathrm{m}}^2{\mathrm{x}}^2$$$${(1+\mathrm{nx})}^{\mathrm{m}}?\sim 1+\mathrm{nmx}+\frac{\mathrm{m})\mathrm{m}-1)}{2}{\mathrm{n}}^2{\mathrm{x}}^2\Rightarrow$$$$\mathrm{f}\left(\mathrm{x}\right)\sim \frac{1+\mathrm{nmx}+\frac{\mathrm{n}(\mathrm{n}-1)}{2}{\mathrm{m}}^2{\mathrm{x}}^2-1-\mathrm{mn}\mathrm{x}-\frac{\mathrm{m}(\mathrm{m}-1)}{2}{\mathrm{n}}^2{\mathrm{x}}^2}{{\mathrm{x}}^2}$$$$\Rightarrow \mathrm{f}\left(\mathrm{x}\right)\sim \frac{{\mathrm{m}}^2\mathrm{n}(\mathrm{n}-1)}{2}-\frac{{\mathrm{n}}^2\mathrm{m}(\mathrm{m}-1)}{2}\Rightarrow$$$$\mathrm{f}\left(\mathrm{x}\right)\sim \frac{\mathrm{mn}(\mathrm{mn}-\mathrm{m})-\mathrm{mn}(\mathrm{nm}-\mathrm{n})}{2}=\frac{\mathrm{mn}}{2}(\mathrm{n}-\mathrm{m})\Rightarrow$$$${\lim }_{\mathrm{x}\to 0}\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{mn}(\mathrm{n}-\mathrm{m})}{2}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com