
Question and Answers Forum
Question Number 121315 by Bird last updated on 06/Nov/20
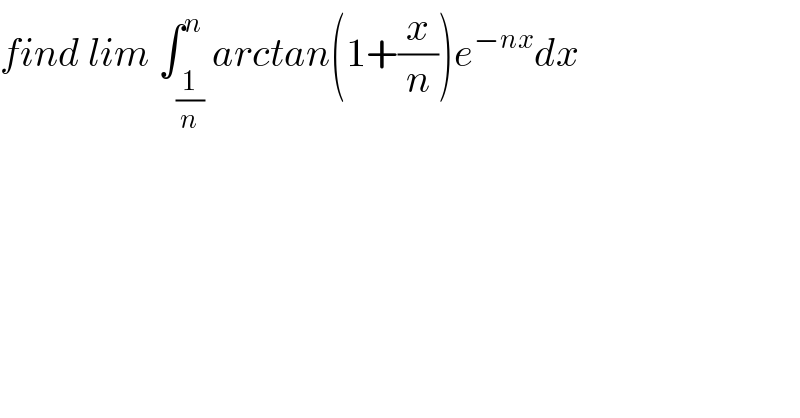
Answered by Lordose last updated on 06/Nov/20
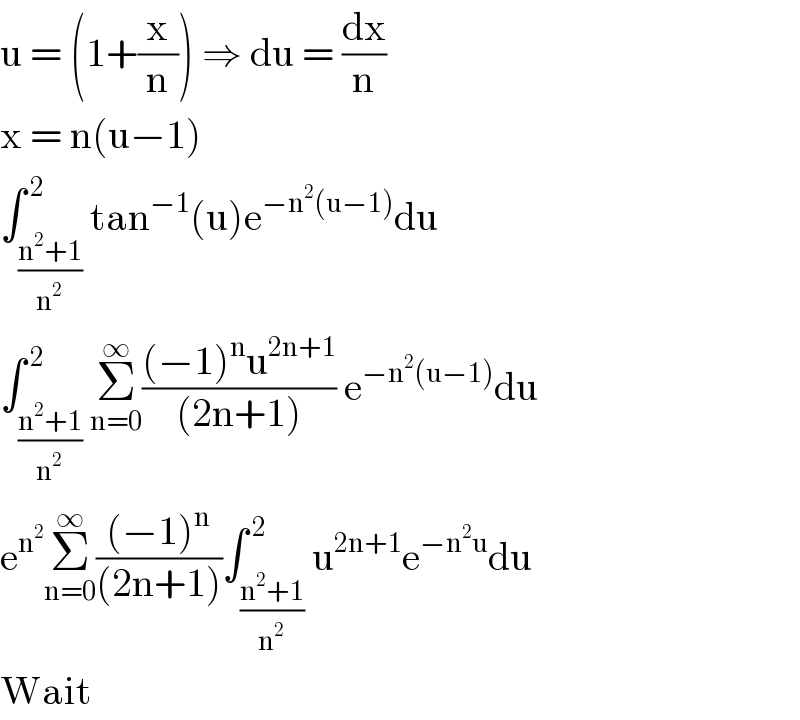
Answered by mathmax by abdo last updated on 06/Nov/20
![A_n =∫_(1/n) ^n arctan(1+(x/n))e^(−nx) dx changement (x/n)=t give A_n =∫_(1/n^2 ) ^1 arctan(1+t)e^(−n^2 t) ndt =n ∫_(1/n^2 ) ^1 arctan(1+t)e^(−n^2 t) dt ⇒(A_n /n) =_(by parts) [−(1/n^2 )e^(−n^2 t) arctan(1+t)]_(1/n^2 ) ^1 +(1/n^2 )∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt =(1/n^2 )e^(−1) arctan(1+(1/n^2 ))−(1/n^2 )e^(−n^2 ) arctan(2)+(1/n^2 )∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt ⇒ A_n =(1/n)e^(−1) arctan(1+(1/n^2 ))−(1/n)e^(−n^2 ) arctan(2)+(1/n)∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt we have lim_(n→+∞) (1/n){e^(−1) arctan(1+(1/n^2 ))−e^(−n^2 arctan2) }=0 ∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt =∫_R f_n (x)dx with f_n (x)=(e^(−n^2 t) /(1+(1+t)^2 )) χ_(](1/n^2 ),1]) (t)dt f_n →^(cs) 0 ⇒(1/n)∫_R f_n (x)dx→0 ⇒lim_(n→+∞) A_n =0](Q121343.png)
| ||
Question and Answers Forum | ||
Question Number 121315 by Bird last updated on 06/Nov/20 | ||
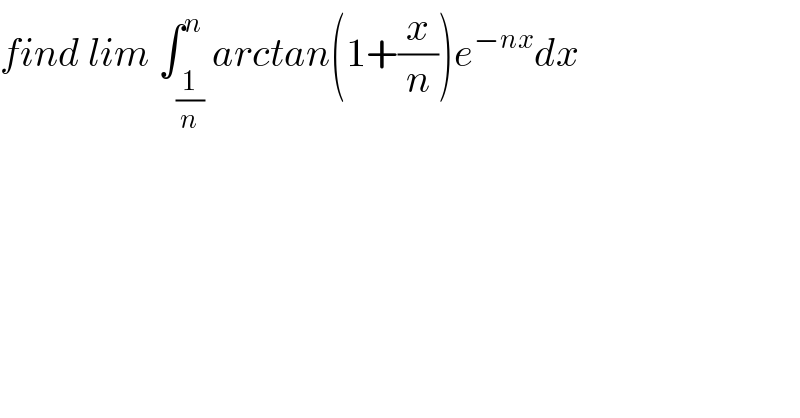 | ||
Answered by Lordose last updated on 06/Nov/20 | ||
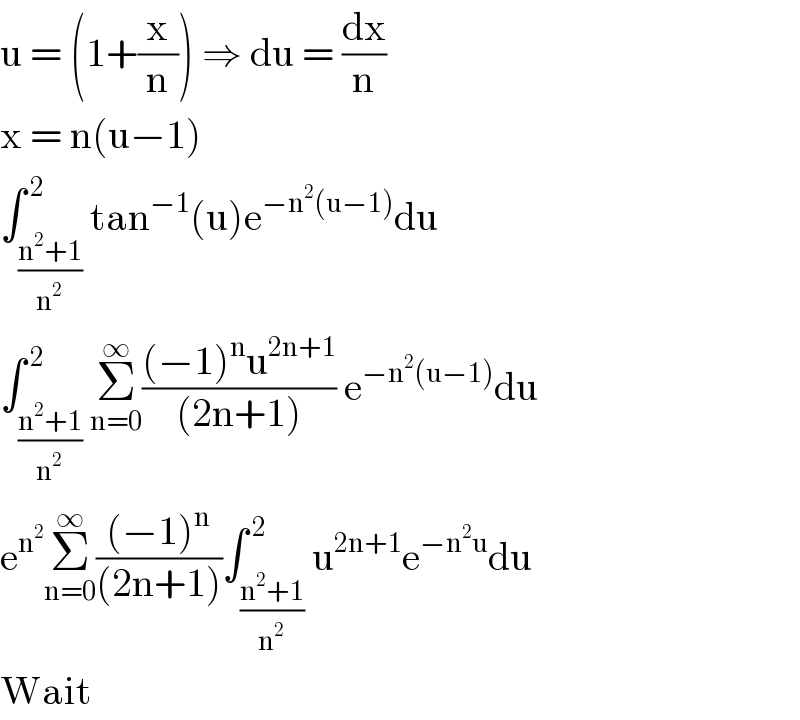 | ||
| ||
Answered by mathmax by abdo last updated on 06/Nov/20 | ||
![A_n =∫_(1/n) ^n arctan(1+(x/n))e^(−nx) dx changement (x/n)=t give A_n =∫_(1/n^2 ) ^1 arctan(1+t)e^(−n^2 t) ndt =n ∫_(1/n^2 ) ^1 arctan(1+t)e^(−n^2 t) dt ⇒(A_n /n) =_(by parts) [−(1/n^2 )e^(−n^2 t) arctan(1+t)]_(1/n^2 ) ^1 +(1/n^2 )∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt =(1/n^2 )e^(−1) arctan(1+(1/n^2 ))−(1/n^2 )e^(−n^2 ) arctan(2)+(1/n^2 )∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt ⇒ A_n =(1/n)e^(−1) arctan(1+(1/n^2 ))−(1/n)e^(−n^2 ) arctan(2)+(1/n)∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt we have lim_(n→+∞) (1/n){e^(−1) arctan(1+(1/n^2 ))−e^(−n^2 arctan2) }=0 ∫_(1/n^2 ) ^1 (e^(−n^2 t) /(1+(1+t)^2 ))dt =∫_R f_n (x)dx with f_n (x)=(e^(−n^2 t) /(1+(1+t)^2 )) χ_(](1/n^2 ),1]) (t)dt f_n →^(cs) 0 ⇒(1/n)∫_R f_n (x)dx→0 ⇒lim_(n→+∞) A_n =0](Q121343.png) | ||
| ||