
Question and Answers Forum
Question Number 12144 by rish@bh last updated on 14/Apr/17
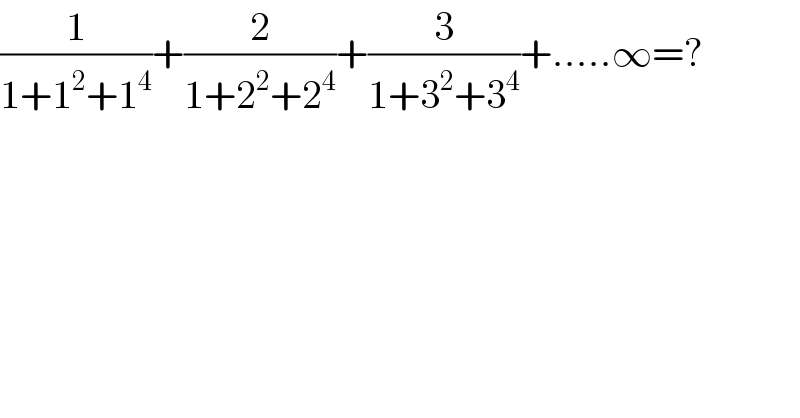
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17
![(n/(n^4 +n^2 +1))=(n/((n^2 +1)^2 −n^2 ))=(n/((n^2 +n+1)(n^2 −n+1)))= (1/2).(((n^2 +n+1)−(n^2 −n+1))/((n^2 +n+1)(n^2 −n+1)))= (1/2)((1/(n^2 −n+1))−(1/(n^2 +n+1))) LHS=(1/2)[(1/1)−(1/3)+(1/3)−(1/7)+(1/7)−(1/(13)).....−(1/(n^2 +n+1))]= =(1/2).(1−(1/(n^2 +n+1)))=((n^2 +n)/(2(n^2 +n+1))) lim_(x→∝) LHS=(1/2) .■](Q12147.png)
Commented by rish@bh last updated on 14/Apr/17

| ||
Question and Answers Forum | ||
Question Number 12144 by rish@bh last updated on 14/Apr/17 | ||
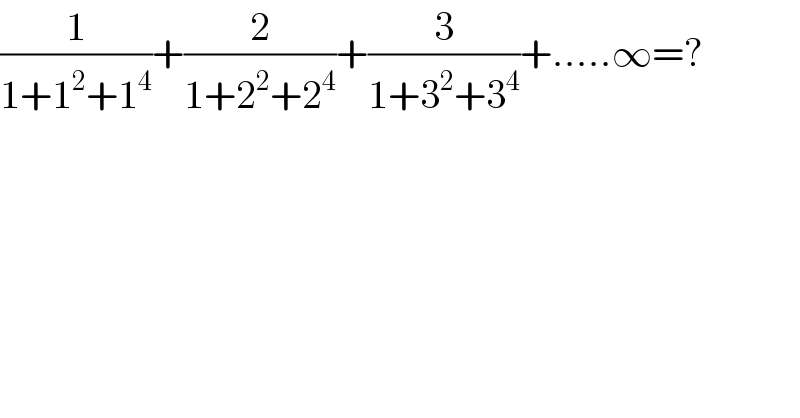 | ||
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 14/Apr/17 | ||
![(n/(n^4 +n^2 +1))=(n/((n^2 +1)^2 −n^2 ))=(n/((n^2 +n+1)(n^2 −n+1)))= (1/2).(((n^2 +n+1)−(n^2 −n+1))/((n^2 +n+1)(n^2 −n+1)))= (1/2)((1/(n^2 −n+1))−(1/(n^2 +n+1))) LHS=(1/2)[(1/1)−(1/3)+(1/3)−(1/7)+(1/7)−(1/(13)).....−(1/(n^2 +n+1))]= =(1/2).(1−(1/(n^2 +n+1)))=((n^2 +n)/(2(n^2 +n+1))) lim_(x→∝) LHS=(1/2) .■](Q12147.png) | ||
| ||
Commented by rish@bh last updated on 14/Apr/17 | ||
 | ||