{ ((x+y=3)),((x^5 +y^5 =33)) :}


Question and Answers Forum

All Questions Topic List
Algebra Questions
Previous in All Question Next in All Question
Previous in Algebra Next in Algebra
Question Number 121449 by liberty last updated on 08/Nov/20
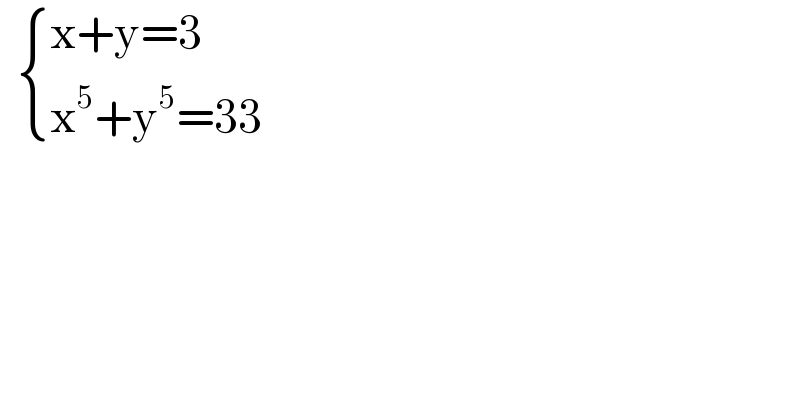
${ ((x+y=3)),((x^5 +y^5 =33)) :}$
${\begin{cases} x + y = 3 \\ x^{5} + y^{5} = 33 \end{cases}$
Commented by Dwaipayan Shikari last updated on 08/Nov/20

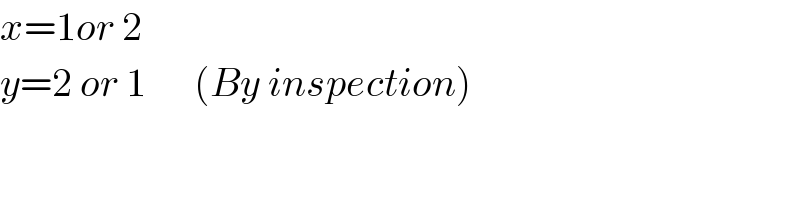
$x = 1 o r 2$ $y = 2 o r 1 (B y i n s p e c t i o n)$
	Answered by MJS_new last updated on 08/Nov/20

	$x + y = a$ $x^{5} + y^{5} = b$ $let x = u - v \land y = u + v$ $(1) 2 u = a \Rightarrow u = \frac{a}{2}$ $insert in (2)$ $5 {a v}^{4} + \frac{5 a^{3}}{2} v^{2} + \frac{a^{5}}{16} = b$ $v^{4} + \frac{a^{2}}{2} v^{2} + \frac{a^{5} - 16 b}{80 a} = 0$ $v = \pm \sqrt{- \frac{a^{2}}{4} \pm \frac{\sqrt{5 (a^{5} + 4 b)}}{10 \sqrt{a}}} [4 solutions]$ $in this case$ $u = \frac{3}{2} \land (v = \pm \frac{1}{2} \lor v = \pm \frac{\sqrt{19}}{2} i)$
	Commented by liberty last updated on 08/Nov/20

	$yes . .$
	Answered by bramlexs22 last updated on 08/Nov/20
	$let x+y=u=3 ∧xy=v (x+y)^5 =x^5 +5x^4 y+10x^3 y^2 +10x^2 y^3 +5xy^4 +y^5 ⇔243=33+5xy(x^3 +y^3 )+10(xy)^2 (x+y) ⇒210=5v((x+y)^3 −3xy(x+y))+30v^2 ⇒210=5v(27−9v)+30v^2 ⇒42=27v−9v^2 +6v^2 ⇒3v^2 −9v+14=0 → { ((v=2)),((v=7)) :} case(1) v=2 ∧u=3 ⇒xy=2 ∧x+y=3 → { ((x=2∧y=1)),((x=1∧y=2)) :} case(2) xy=7 ∧x+y=3 ⇒x(3−x)=7 , x^2 −3x+7=0 → { ((x=((3+i(√(19)))/2) →y=((3−i(√(19)))/2))),((x=((3−i(√(19)))/2)→y=((3+i(√(19)))/2))) :}$
	$let x + y = u = 3 \land xy = v$ ${(x + y)}^{5} = x^{5} + {5 x}^{4} y + {10 x}^{3} y^{2} + {10 x}^{2} y^{3} + {5 xy}^{4} + y^{5}$ $\Leftrightarrow 243 = 33 + 5 xy (x^{3} + y^{3}) + 10 {(xy)}^{2} (x + y)$ $\Rightarrow 210 = 5 v ({(x + y)}^{3} - 3 xy (x + y)) + {30 v}^{2}$ $\Rightarrow 210 = 5 v (27 - 9 v) + {30 v}^{2}$ $\Rightarrow 42 = 27 v - {9 v}^{2} + {6 v}^{2}$ $\Rightarrow {3 v}^{2} - 9 v + 14 = 0 \to {\begin{cases} v = 2 \\ v = 7 \end{cases}$ $case (1) v = 2 \land u = 3$ $\Rightarrow xy = 2 \land x + y = 3 \to {\begin{cases} x = 2 \land y = 1 \\ x = 1 \land y = 2 \end{cases}$ $case (2) xy = 7 \land x + y = 3$ $\Rightarrow x (3 - x) = 7, x^{2} - 3 x + 7 = 0$ $\to {\begin{cases} x = \frac{3 + i \sqrt{19}}{2} \to y = \frac{3 - i \sqrt{19}}{2} \\ x = \frac{3 - i \sqrt{19}}{2} \to y = \frac{3 + i \sqrt{19}}{2} \end{cases}$
	Commented by liberty last updated on 08/Nov/20

	$gave kudos$
	Answered by mr W last updated on 08/Nov/20

	${(x + y)}^{5} = x^{5} + 5 x^{4} y + 10 x^{3} y^{2} + 10 x^{2} y^{3} + 5 {x y}^{4} + y^{5}$ $3^{5} = 33 + 5 x y (x^{3} + 2 x^{2} y + 2 {x y}^{2} + y^{3})$ $3^{5} = 33 + 5 x y [x^{3} + 3 x^{2} y + 3 {x y}^{2} + y^{3} - x y (x + y)]$ $3^{5} = 33 + 5 x y [{(x + y)}^{3} - x y (x + y)]$ $3^{5} = 33 + 5 x y (3^{3} - 3 x y)$ $14 = x y (9 - x y)$ ${(x y)}^{2} - 9 (x y) + 14 = 0$ $(x y - 2) (x y - 7) = 0$ $\Rightarrow x y = 2 o r 7$ $z^{2} - 3 z + 2 = 0 \Rightarrow (x, y) = 1, 2$ $z^{2} - 3 z + 7 = 0 \Rightarrow (x, y) = \frac{3 + i \sqrt{19}}{2}, \frac{3 - i \sqrt{19}}{2}$
	Commented by liberty last updated on 08/Nov/20

	$yess . . .$
	Commented by harckinwunmy last updated on 08/Nov/20

	$ff$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum