Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 121539 by ajfour last updated on 09/Nov/20

Commented by ajfour last updated on 09/Nov/20

Find (s/R) for maximum blue triangular area. (square remains within semicircle)

$$\:\:\:\:\:\:\:\:{Find}\:\frac{{s}}{{R}}\:\:{for}\:{maximum}\:{blue} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{triangular}\:{area}. \\ $$$$\left({square}\:{remains}\:{within}\:{semicircle}\right) \\ $$

Answered by mr W last updated on 09/Nov/20

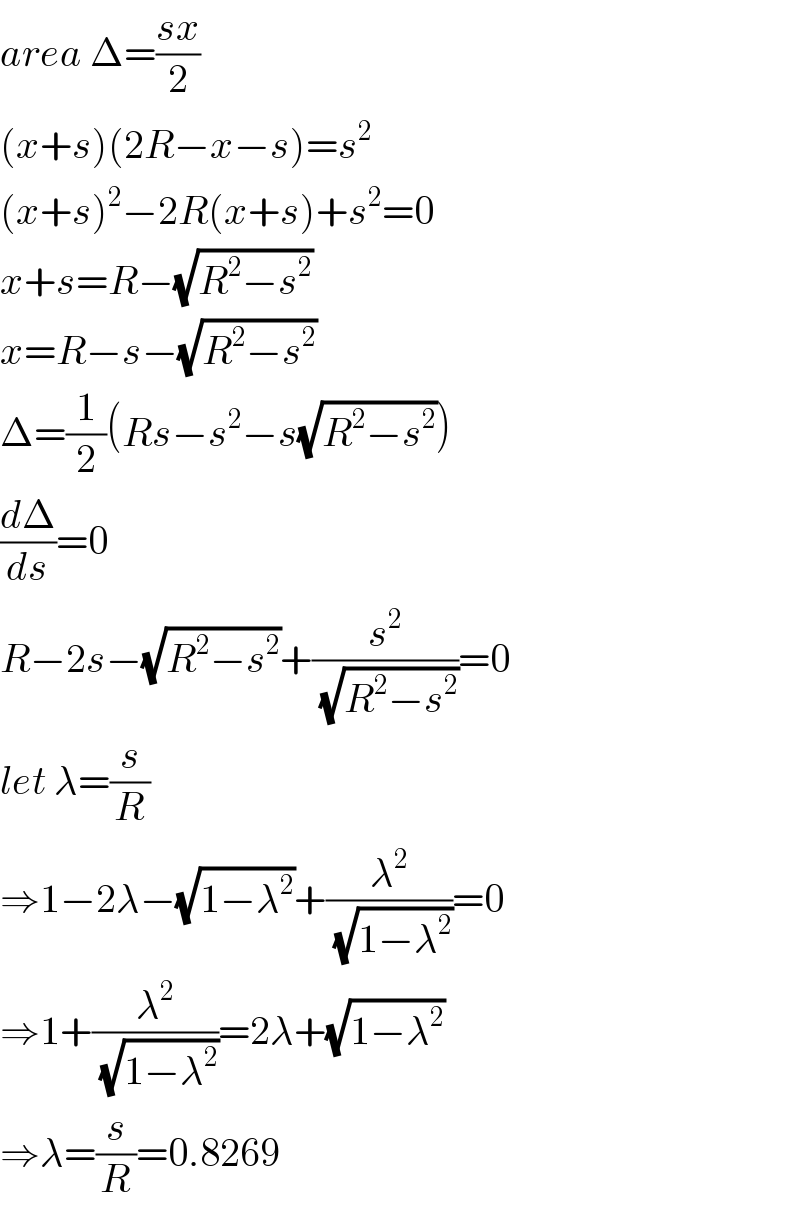
area Δ=((sx)/2) (x+s)(2R−x−s)=s^2 (x+s)^2 −2R(x+s)+s^2 =0 x+s=R−(√(R^2 −s^2 )) x=R−s−(√(R^2 −s^2 )) Δ=(1/2)(Rs−s^2 −s(√(R^2 −s^2 ))) (dΔ/ds)=0 R−2s−(√(R^2 −s^2 ))+(s^2 /( (√(R^2 −s^2 ))))=0 let λ=(s/R) ⇒1−2λ−(√(1−λ^2 ))+(λ^2 /( (√(1−λ^2 ))))=0 ⇒1+(λ^2 /( (√(1−λ^2 ))))=2λ+(√(1−λ^2 )) ⇒λ=(s/R)=0.8269

$${area}\:\Delta=\frac{{sx}}{\mathrm{2}} \\ $$$$\left({x}+{s}\right)\left(\mathrm{2}{R}−{x}−{s}\right)={s}^{\mathrm{2}} \\ $$$$\left({x}+{s}\right)^{\mathrm{2}} −\mathrm{2}{R}\left({x}+{s}\right)+{s}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}+{s}={R}−\sqrt{{R}^{\mathrm{2}} −{s}^{\mathrm{2}} } \\ $$$${x}={R}−{s}−\sqrt{{R}^{\mathrm{2}} −{s}^{\mathrm{2}} } \\ $$$$\Delta=\frac{\mathrm{1}}{\mathrm{2}}\left({Rs}−{s}^{\mathrm{2}} −{s}\sqrt{{R}^{\mathrm{2}} −{s}^{\mathrm{2}} }\right) \\ $$$$\frac{{d}\Delta}{{ds}}=\mathrm{0} \\ $$$${R}−\mathrm{2}{s}−\sqrt{{R}^{\mathrm{2}} −{s}^{\mathrm{2}} }+\frac{{s}^{\mathrm{2}} }{\:\sqrt{{R}^{\mathrm{2}} −{s}^{\mathrm{2}} }}=\mathrm{0} \\ $$$${let}\:\lambda=\frac{{s}}{{R}} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{2}\lambda−\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }+\frac{\lambda^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}+\frac{\lambda^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }}=\mathrm{2}\lambda+\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\Rightarrow\lambda=\frac{{s}}{{R}}=\mathrm{0}.\mathrm{8269} \\ $$

Commented by mr W last updated on 09/Nov/20

yes sir, you are right!

$${yes}\:{sir},\:{you}\:{are}\:{right}! \\ $$

Commented by ajfour last updated on 09/Nov/20

Thank you sir. i think you have checked when is the area a maximum for we get two positive values of lambda.

Commented by ajfour last updated on 09/Nov/20

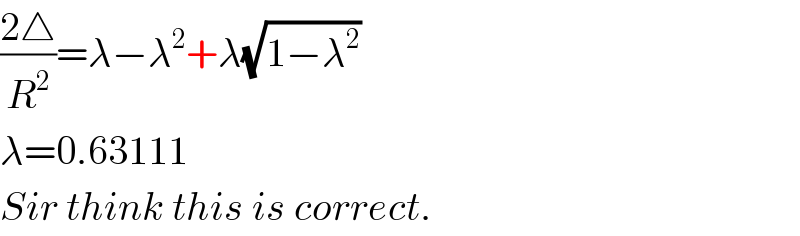
((2△)/R^2 )=λ−λ^2 +λ(√(1−λ^2 )) λ=0.63111 Sir think this is correct.

$$\frac{\mathrm{2}\bigtriangleup}{{R}^{\mathrm{2}} }=\lambda−\lambda^{\mathrm{2}} +\lambda\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\lambda=\mathrm{0}.\mathrm{63111} \\ $$$${Sir}\:{think}\:{this}\:{is}\:{correct}. \\ $$

Commented by ajfour last updated on 09/Nov/20

Answered by ajfour last updated on 09/Nov/20

Commented by ajfour last updated on 09/Nov/20

s=2Rsin θcos θ ; x=2Rcos^2 θ−s 2△=sx let (s/R)=λ = sin 2θ 2△=(Rsin 2θ)(2Rcos^2 θ−Rsin 2θ) ((2△)/R^2 )=sin 2θ(1+cos 2θ−sin 2θ) (d/dθ)(((2△)/R^2 ))=0 ⇒ 2cos 2θ(1+cos 2θ−sin 2θ) =sin 2θ(2cos 2θ+2sin 2θ) ⇒ cos 2θ+cos^2 2θ=2cos 2θsin 2θ +sin^2 2θ with sin 2θ=λ (1−λ^2 )(1−2λ)^2 =(2λ^2 −1)^2 ⇒ 4λ^2 −4λ^4 −4λ+4λ^3 +1−λ^2 =4λ^4 −4λ^2 +1 ⇒ 8λ^3 −4λ^2 −7λ+4=0 λ=0.82694 , 0.63111 I think λ=(s/R)=0.63111 should be the appropriate answer.

$${s}=\mathrm{2}{R}\mathrm{sin}\:\theta\mathrm{cos}\:\theta\:\:;\:\:\:{x}=\mathrm{2}{R}\mathrm{cos}\:^{\mathrm{2}} \theta−{s} \\ $$$$\mathrm{2}\bigtriangleup={sx} \\ $$$${let}\:\:\:\frac{{s}}{{R}}=\lambda\:=\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\mathrm{2}\bigtriangleup=\left({R}\mathrm{sin}\:\mathrm{2}\theta\right)\left(\mathrm{2}{R}\mathrm{cos}\:^{\mathrm{2}} \theta−{R}\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\frac{\mathrm{2}\bigtriangleup}{{R}^{\mathrm{2}} }=\mathrm{sin}\:\mathrm{2}\theta\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\frac{{d}}{{d}\theta}\left(\frac{\mathrm{2}\bigtriangleup}{{R}^{\mathrm{2}} }\right)=\mathrm{0}\:\:\:\Rightarrow \\ $$$$\mathrm{2cos}\:\mathrm{2}\theta\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta−\mathrm{sin}\:\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:=\mathrm{sin}\:\mathrm{2}\theta\left(\mathrm{2cos}\:\mathrm{2}\theta+\mathrm{2sin}\:\mathrm{2}\theta\right) \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}\:^{\mathrm{2}} \mathrm{2}\theta=\mathrm{2cos}\:\mathrm{2}\theta\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}\theta \\ $$$${with}\:\:\mathrm{sin}\:\mathrm{2}\theta=\lambda \\ $$$$\:\:\:\:\:\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}\lambda\right)^{\mathrm{2}} =\left(\mathrm{2}\lambda^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{4}\lambda^{\mathrm{4}} −\mathrm{4}\lambda+\mathrm{4}\lambda^{\mathrm{3}} +\mathrm{1}−\lambda^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}\lambda^{\mathrm{4}} −\mathrm{4}\lambda^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow\:\:\mathrm{8}\lambda^{\mathrm{3}} −\mathrm{4}\lambda^{\mathrm{2}} −\mathrm{7}\lambda+\mathrm{4}=\mathrm{0} \\ $$$$\:\:\:\:\:\lambda=\mathrm{0}.\mathrm{82694}\:\:\:,\:\:\:\mathrm{0}.\mathrm{63111} \\ $$$${I}\:{think}\:\:\lambda=\frac{{s}}{{R}}=\mathrm{0}.\mathrm{63111}\:\:{should}\: \\ $$$${be}\:{the}\:\:{appropriate}\:{answer}. \\ $$$$ \\ $$

Answered by MJS_new last updated on 09/Nov/20

let R=1 semicircle: y=(√(1−x^2 )) s= (√(1−p^2 )) base of triangle ∣p−1+(√(1−p^2 ))∣ 2×area of triangle is ∣p−1+(√(1−p^2 ))∣(√(1−p^2 )) its maximum is at p≈−.775694 ⇒ s≈.631109

$$\mathrm{let}\:{R}=\mathrm{1} \\ $$$$\mathrm{semicircle}:\:{y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${s}=\:\sqrt{\mathrm{1}−{p}^{\mathrm{2}} } \\ $$$$\mathrm{base}\:\mathrm{of}\:\mathrm{triangle}\:\mid{p}−\mathrm{1}+\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\mid \\ $$$$\mathrm{2}×\mathrm{area}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{is}\:\mid{p}−\mathrm{1}+\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\mid\sqrt{\mathrm{1}−{p}^{\mathrm{2}} } \\ $$$$\mathrm{its}\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:{p}\approx−.\mathrm{775694} \\ $$$$\Rightarrow\:{s}\approx.\mathrm{631109} \\ $$

Commented by MJS_new last updated on 09/Nov/20

please check...

$$\mathrm{please}\:\mathrm{check}... \\ $$

Commented by ajfour last updated on 09/Nov/20

Commented by ajfour last updated on 09/Nov/20

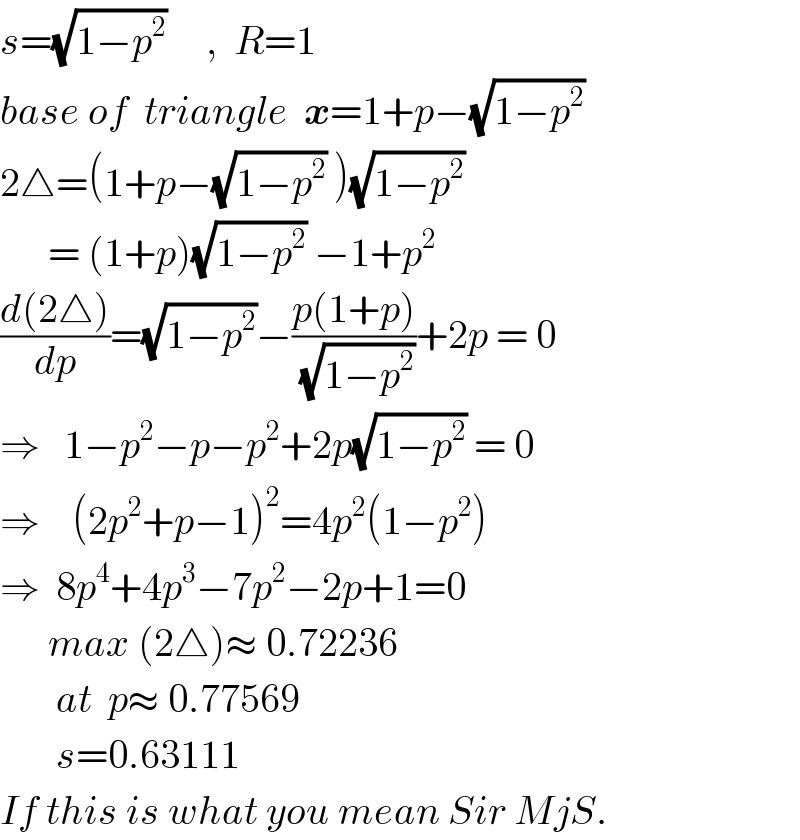
s=(√(1−p^2 )) , R=1 base of triangle x=1+p−(√(1−p^2 )) 2△=(1+p−(√(1−p^2 )) )(√(1−p^2 )) = (1+p)(√(1−p^2 )) −1+p^2 ((d(2△))/dp)=(√(1−p^2 ))−((p(1+p))/( (√(1−p^2 ))))+2p = 0 ⇒ 1−p^2 −p−p^2 +2p(√(1−p^2 )) = 0 ⇒ (2p^2 +p−1)^2 =4p^2 (1−p^2 ) ⇒ 8p^4 +4p^3 −7p^2 −2p+1=0 max (2△)≈ 0.72236 at p≈ 0.77569 s=0.63111 If this is what you mean Sir MjS.

$${s}=\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\:\:\:\:\:,\:\:{R}=\mathrm{1} \\ $$$${base}\:{of}\:\:{triangle}\:\:\boldsymbol{{x}}=\mathrm{1}+{p}−\sqrt{\mathrm{1}−{p}^{\mathrm{2}} } \\ $$$$\mathrm{2}\bigtriangleup=\left(\mathrm{1}+{p}−\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\:\right)\sqrt{\mathrm{1}−{p}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:=\:\left(\mathrm{1}+{p}\right)\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\:−\mathrm{1}+{p}^{\mathrm{2}} \\ $$$$\frac{{d}\left(\mathrm{2}\bigtriangleup\right)}{{dp}}=\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }−\frac{{p}\left(\mathrm{1}+{p}\right)}{\:\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }}+\mathrm{2}{p}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\mathrm{1}−{p}^{\mathrm{2}} −{p}−{p}^{\mathrm{2}} +\mathrm{2}{p}\sqrt{\mathrm{1}−{p}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\left(\mathrm{2}{p}^{\mathrm{2}} +{p}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}{p}^{\mathrm{2}} \left(\mathrm{1}−{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\:\:\mathrm{8}{p}^{\mathrm{4}} +\mathrm{4}{p}^{\mathrm{3}} −\mathrm{7}{p}^{\mathrm{2}} −\mathrm{2}{p}+\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:{max}\:\left(\mathrm{2}\bigtriangleup\right)\approx\:\mathrm{0}.\mathrm{72236} \\ $$$$\:\:\:\:\:\:\:{at}\:\:{p}\approx\:\mathrm{0}.\mathrm{77569} \\ $$$$\:\:\:\:\:\:\:{s}=\mathrm{0}.\mathrm{63111} \\ $$$${If}\:{this}\:{is}\:{what}\:{you}\:{mean}\:{Sir}\:{MjS}. \\ $$

Commented by ajfour last updated on 09/Nov/20

Commented by MJS_new last updated on 09/Nov/20

yes thank you, typo while approximating the zero. I have corrected it

$$\mathrm{yes}\:\mathrm{thank}\:\mathrm{you},\:\mathrm{typo}\:\mathrm{while}\:\mathrm{approximating}\:\mathrm{the} \\ $$$$\mathrm{zero}.\:\mathrm{I}\:\mathrm{have}\:\mathrm{corrected}\:\mathrm{it} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com