
Question and Answers Forum
Question Number 121548 by benjo_mathlover last updated on 09/Nov/20
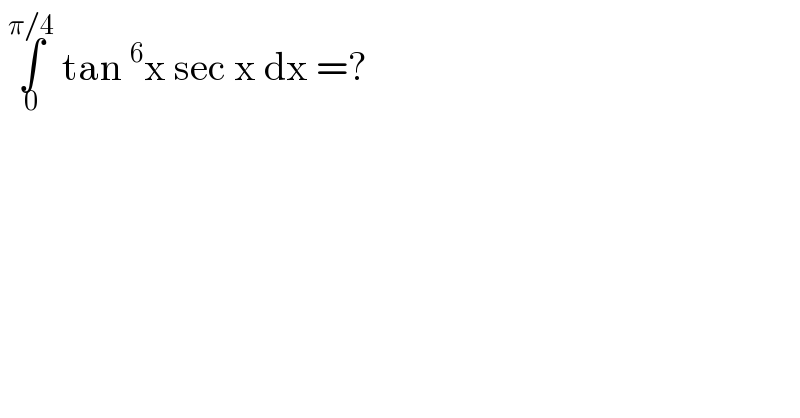
Answered by MJS_new last updated on 09/Nov/20
![∫tan^6 x sec x dx=∫((sin^6 x)/(cos^7 x))dx= [t=(1/(sin x)) → dx=−((sin^2 x)/(cos x))] =−∫(dt/((t^2 −1)^4 ))= [Ostrogradski′s Method] =((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(16))∫(dt/(t^2 −1))= =((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(32))ln ∣((t−1)/(t+1))∣ the borders are x∈[0; (π/4)] ⇔ t∈]+∞; (√2)] ⇒ answer is −[((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(32))ln ∣((t−1)/(t+1))∣]_(√2) ^(+∞) = =((13(√2))/(48))+(5/(16))ln (−1+(√2))](Q121551.png)
Commented by liberty last updated on 09/Nov/20

Commented by Fareed last updated on 09/Nov/20
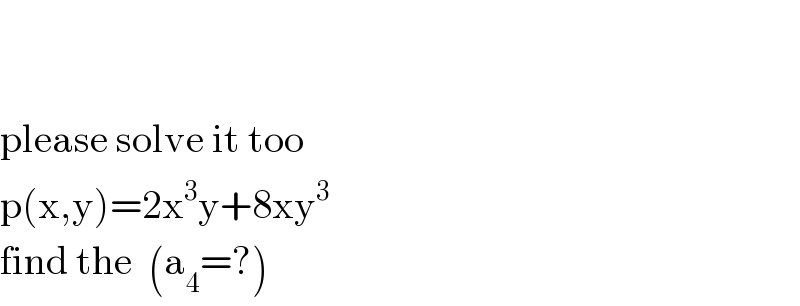
| ||
Question and Answers Forum | ||
Question Number 121548 by benjo_mathlover last updated on 09/Nov/20 | ||
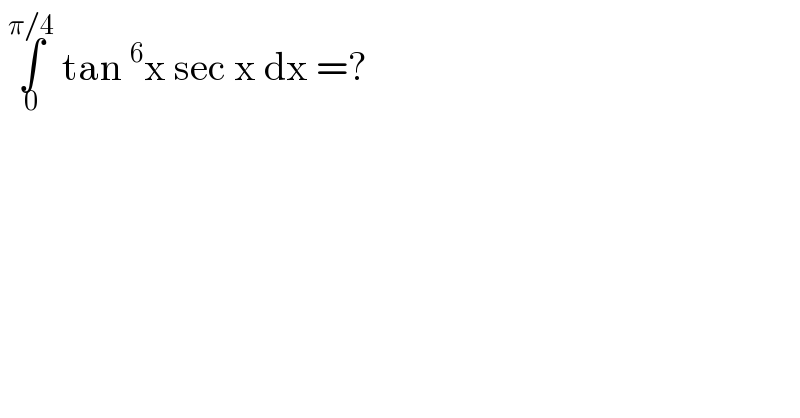 | ||
Answered by MJS_new last updated on 09/Nov/20 | ||
![∫tan^6 x sec x dx=∫((sin^6 x)/(cos^7 x))dx= [t=(1/(sin x)) → dx=−((sin^2 x)/(cos x))] =−∫(dt/((t^2 −1)^4 ))= [Ostrogradski′s Method] =((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(16))∫(dt/(t^2 −1))= =((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(32))ln ∣((t−1)/(t+1))∣ the borders are x∈[0; (π/4)] ⇔ t∈]+∞; (√2)] ⇒ answer is −[((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(32))ln ∣((t−1)/(t+1))∣]_(√2) ^(+∞) = =((13(√2))/(48))+(5/(16))ln (−1+(√2))](Q121551.png) | ||
| ||
Commented by liberty last updated on 09/Nov/20 | ||
 | ||
Commented by Fareed last updated on 09/Nov/20 | ||
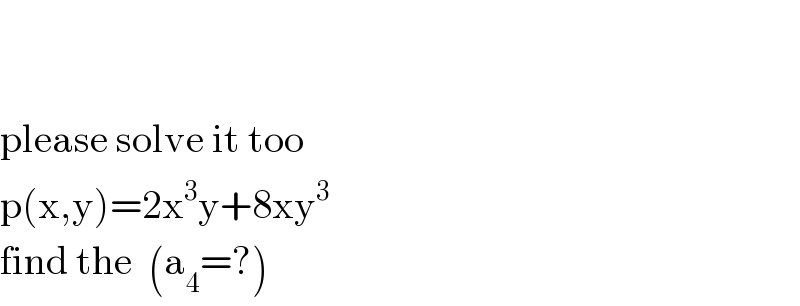 | ||