Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 121601 by benjo_mathlover last updated on 09/Nov/20

∫ (dx/(x (√(3+x^2 )))) ?

$$\:\:\int\:\frac{\mathrm{dx}}{\mathrm{x}\:\sqrt{\mathrm{3}+\mathrm{x}^{\mathrm{2}} }}\:? \\ $$

Answered by liberty last updated on 10/Nov/20

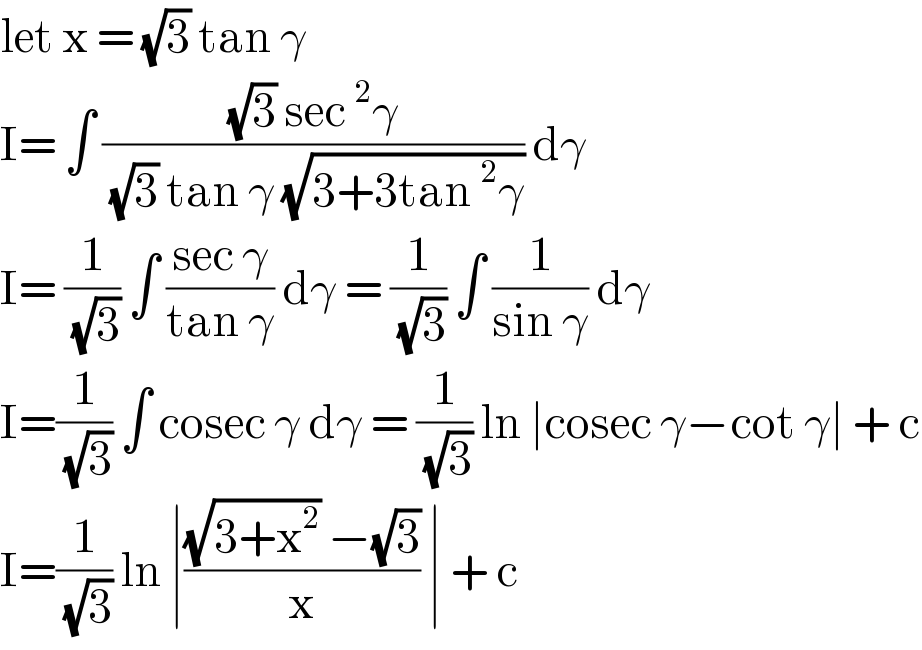
let x = (√3) tan γ I= ∫ (((√3) sec^2 γ)/( (√3) tan γ (√(3+3tan^2 γ)))) dγ I= (1/( (√3))) ∫ ((sec γ)/(tan γ)) dγ = (1/( (√3))) ∫ (1/(sin γ)) dγ I=(1/( (√3))) ∫ cosec γ dγ = (1/( (√3))) ln ∣cosec γ−cot γ∣ + c I=(1/( (√3))) ln ∣(((√(3+x^2 )) −(√3))/x) ∣ + c

$$\mathrm{let}\:\mathrm{x}\:=\:\sqrt{\mathrm{3}}\:\mathrm{tan}\:\gamma\: \\ $$$$\mathrm{I}=\:\int\:\frac{\sqrt{\mathrm{3}}\:\mathrm{sec}\:^{\mathrm{2}} \gamma}{\:\sqrt{\mathrm{3}}\:\mathrm{tan}\:\gamma\:\sqrt{\mathrm{3}+\mathrm{3tan}\:^{\mathrm{2}} \gamma}}\:\mathrm{d}\gamma \\ $$$$\mathrm{I}=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\int\:\frac{\mathrm{sec}\:\gamma}{\mathrm{tan}\:\gamma}\:\mathrm{d}\gamma\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\int\:\frac{\mathrm{1}}{\mathrm{sin}\:\gamma}\:\mathrm{d}\gamma \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\int\:\mathrm{cosec}\:\gamma\:\mathrm{d}\gamma\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\mid\mathrm{cosec}\:\gamma−\mathrm{cot}\:\gamma\mid\:+\:\mathrm{c} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{3}+\mathrm{x}^{\mathrm{2}} }\:−\sqrt{\mathrm{3}}}{\mathrm{x}}\:\mid\:+\:\mathrm{c}\: \\ $$

Answered by Olaf last updated on 10/Nov/20

x = (√3)sinhu I = ∫(((√3)coshu)/( (√3)sinhu(√(3+3sinh^2 u))))du I = (1/( (√3)))∫(du/( sinhu)) I = (1/( (√3)))∫(du/( ((e^u −e^(−u) )/2))) I = (2/( (√3)))∫((e^u du)/(e^(2u) −1)) I = (1/( (√3)))∫[(1/(e^u −1))−(1/(e^u +1))]e^u du I = (1/( (√3)))ln∣((e^u −1)/(e^u +1))∣ I = (1/( (√3)))ln∣((e^(u/2) −e^(−u/2) )/(e^(u/2) +e^(−u/2) ))∣ I = (1/( (√3)))ln∣tanh((u/2))∣ I = (1/( (√3)))ln∣tanh((1/2)argsinh((x/( (√3)))))∣

$${x}\:=\:\sqrt{\mathrm{3}}\mathrm{sinh}{u} \\ $$$$\mathrm{I}\:=\:\int\frac{\sqrt{\mathrm{3}}\mathrm{cosh}{u}}{\:\sqrt{\mathrm{3}}\mathrm{sinh}{u}\sqrt{\mathrm{3}+\mathrm{3sinh}^{\mathrm{2}} {u}}}{du} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\frac{{du}}{\:\mathrm{sinh}{u}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\frac{{du}}{\:\frac{{e}^{{u}} −{e}^{−{u}} }{\mathrm{2}}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}\int\frac{{e}^{{u}} {du}}{{e}^{\mathrm{2}{u}} −\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\left[\frac{\mathrm{1}}{{e}^{{u}} −\mathrm{1}}−\frac{\mathrm{1}}{{e}^{{u}} +\mathrm{1}}\right]{e}^{{u}} {du} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{{e}^{{u}} −\mathrm{1}}{{e}^{{u}} +\mathrm{1}}\mid \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{ln}\mid\frac{{e}^{{u}/\mathrm{2}} −{e}^{−{u}/\mathrm{2}} }{{e}^{{u}/\mathrm{2}} +{e}^{−{u}/\mathrm{2}} }\mid \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{ln}\mid\mathrm{tanh}\left(\frac{{u}}{\mathrm{2}}\right)\mid \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\mathrm{ln}\mid\mathrm{tanh}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{argsinh}\left(\frac{{x}}{\:\sqrt{\mathrm{3}}}\right)\right)\mid \\ $$

Answered by Dwaipayan Shikari last updated on 10/Nov/20

∫(dx/(x(√(3+x^2 )))) ∫((sec^2 θ)/( (√3)tanθ secθ))dθ x=(√3)tanθ =(1/( (√3)))∫(1/(sinθ))dθ=(1/3)log(tan(θ/2))+C =(1/( (√3)))log(((−(√3)+(√(3+x^2 )))/( x)))+C

$$\int\frac{{dx}}{{x}\sqrt{\mathrm{3}+{x}^{\mathrm{2}} }} \\ $$$$\int\frac{{sec}^{\mathrm{2}} \theta}{\:\sqrt{\mathrm{3}}{tan}\theta\:{sec}\theta}{d}\theta\:\:\:\:\:\:\:{x}=\sqrt{\mathrm{3}}{tan}\theta \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int\frac{\mathrm{1}}{{sin}\theta}{d}\theta=\frac{\mathrm{1}}{\mathrm{3}}{log}\left({tan}\frac{\theta}{\mathrm{2}}\right)+{C}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{log}\left(\frac{−\sqrt{\mathrm{3}}+\sqrt{\mathrm{3}+{x}^{\mathrm{2}} }}{\:{x}}\right)+{C} \\ $$

Answered by TANMAY PANACEA last updated on 10/Nov/20

∫((xdx)/(x^2 (√(3+x^2 )) )) t^2 =3+x^2 →2tdt=xdx ∫((tdt)/((t^2 −3)×t))=∫(dt/(t^2 −3)) =(1/(2(√3)))ln(((t−(√3))/(t+(√3))))+c =(1/(2(√3)))ln((((√(3+x^2 )) −(√3))/( (√(3+x^2 )) +(√3))))+c

$$\int\frac{{xdx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{3}+{x}^{\mathrm{2}} }\:} \\ $$$${t}^{\mathrm{2}} =\mathrm{3}+{x}^{\mathrm{2}} \rightarrow\mathrm{2}{tdt}={xdx} \\ $$$$\int\frac{{tdt}}{\left({t}^{\mathrm{2}} −\mathrm{3}\right)×{t}}=\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{{t}−\sqrt{\mathrm{3}}}{{t}+\sqrt{\mathrm{3}}}\right)+{c} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{ln}\left(\frac{\sqrt{\mathrm{3}+{x}^{\mathrm{2}} }\:−\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{3}+{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{3}}}\right)+{c} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com